一種物理主機虛擬內存分析方法及裝置與流程
2023-05-12 03:15:11 2
本發明涉及虛擬內存技術領域,特別是涉及一種物理主機虛擬內存分析方法及裝置。
背景技術:
目前,物理主機虛擬內存在主機中使用廣泛,也起著非常重要的作用,但是一般在對物理主機虛擬內存進行分析的過程中,需要分析虛擬內存的大小,但是每次檢測到的物理主機虛擬內存的數據非常多,無法獲取物理主機虛擬內存局部最優解,無法獲取更精確的虛擬內存的大小,且採用通用算法獲取局部最優解的複雜度較高。
技術實現要素:
本發明的目的是提供一種物理主機虛擬內存分析方法及裝置,以實現降低複雜度。
為解決上述技術問題,本發明提供一種物理主機虛擬內存分析方法,該方法包括:
步驟1、隨機選擇多個染色體作為初始值輸入至遺傳算法,得到最優的兩條作為父母染色體;所述多個染色體為物理主機虛擬內存數據;
步驟2、根據父母染色體產生多個孩子染色體;
步驟3、評估每個孩子染色體所對應個體的適應度,將孩子染色體傳入遺傳算法中,從種群中選擇出最優的兩個計算結果作為新的父母染色體;
步驟4、重複步驟2至步驟3,直至獲取到最優解,將最優解作為物理主機虛擬內存局部最優解。
優選的,所述根據父母染色體產生多個孩子染色體,包括:
獲取染色體的平均值,方差,期望,部分交叉和父母個體,產生一個孩子染色體的集合。
優選的,所述評估每個孩子染色體所對應個體的適應度之後,還包括:
在孩子染色體中去除不符合適應度要求的染色體。
優選的,所述將孩子染色體傳入遺傳算法中之前,還包括:
對孩子染色體進行交叉操作和變異操作。
本發明還提供一種物理主機虛擬內存分析裝置,用於實現物理主機虛擬內存分析方法,該裝置包括:
選擇模塊,用於隨機選擇多個染色體作為初始值輸入至遺傳算法,得到最優的兩條作為父母染色體;所述多個染色體為物理主機虛擬內存數據;
生產模塊,用於根據父母染色體產生多個孩子染色體;
評估模塊,用於評估每個孩子染色體所對應個體的適應度,將孩子染色體傳入遺傳算法中,從種群中選擇出最優的兩個計算結果作為新的父母染色體;
重複模塊,用於重複調用生產模塊和評估模塊,直至獲取到最優解,將最優解作為物理主機虛擬內存局部最優解。
優選的,所述生產模塊具體用於獲取染色體的平均值,方差,期望,部分交叉和父母個體,產生一個孩子染色體的集合。
優選的,所述評估模塊還包括:去除單元,用於在孩子染色體中去除不符合適應度要求的染色體。
優選的,所述評估模塊還包括:操作單元,用於對孩子染色體進行交叉操作和變異操作。
本發明所提供的一種物理主機虛擬內存分析方法及裝置,步驟1、隨機選擇多個染色體作為初始值輸入至遺傳算法,得到最優的兩條作為父母染色體;所述多個染色體為物理主機虛擬內存數據;步驟2、根據父母染色體產生多個孩子染色體;步驟3、評估每個孩子染色體所對應個體的適應度,將孩子染色體傳入遺傳算法中,從種群中選擇出最優的兩個計算結果作為新的父母染色體;步驟4、重複步驟2至步驟3,直至獲取到最優解,將最優解作為物理主機虛擬內存局部最優解。可見,採用遺傳算法確定物理主機虛擬內存局部最優解,彌補了普通算法尋找局部最優解題的不足和以往經驗數據引起的誤差,本發明採用高度非線性的方式,並實現給出局部最優解,大大降低了獲取最優解的複雜度,並且評估每個孩子染色體所對應個體的適應度,將孩子染色體傳入遺傳算法中,有效提高了虛擬內存大小和物理主機的適配度。
附圖說明
為了更清楚地說明本發明實施例或現有技術中的技術方案,下面將對實施例或現有技術描述中所需要使用的附圖作簡單地介紹,顯而易見地,下面描述中的附圖僅僅是本發明的實施例,對於本領域普通技術人員來講,在不付出創造性勞動的前提下,還可以根據提供的附圖獲得其他的附圖。
圖 1為本發明所提供的一種物理主機虛擬內存分析方法的流程圖;
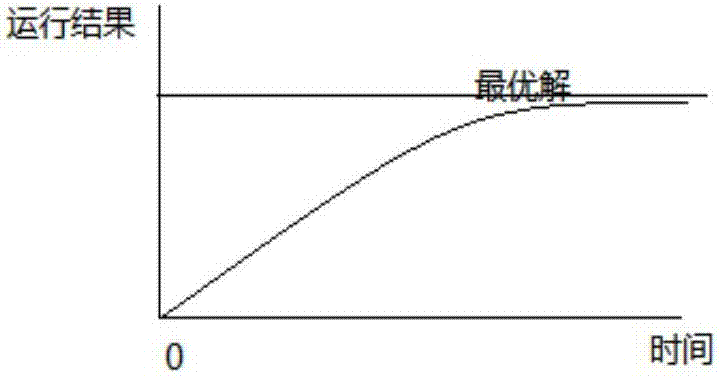
圖2為遺傳算法的運行時間和運行結果示意圖;
圖3為本發明所提供的一種物理主機虛擬內存分析裝置的結構示意圖。
具體實施方式
本發明的核心是提供一種物理主機虛擬內存分析方法及裝置,以實現降低複雜度。
為了使本技術領域的人員更好地理解本發明方案,下面將結合本發明實施例中的附圖,對本發明實施例中的技術方案進行清楚、完整地描述,顯然,所描述的實施例僅僅是本發明一部分實施例,而不是全部的實施例。基於本發明中的實施例,本領域普通技術人員在沒有做出創造性勞動前提下所獲得的所有其他實施例,都屬於本發明保護的範圍。
請參考圖1,圖1為本發明所提供的一種物理主機虛擬內存分析方法的流程圖,該方法包括:
步驟1、隨機選擇多個染色體作為初始值輸入至遺傳算法,得到最優的兩條作為父母染色體;
其中,所述多個染色體為物理主機虛擬內存數據;
步驟2、根據父母染色體產生多個孩子染色體;
步驟3、評估每個孩子染色體所對應個體的適應度,將孩子染色體傳入遺傳算法中,從種群中選擇出最優的兩個計算結果作為新的父母染色體;
步驟4、重複步驟2至步驟3,直至獲取到最優解,將最優解作為物理主機虛擬內存局部最優解。
可見,該方法採用遺傳算法確定物理主機虛擬內存局部最優解,彌補了普通算法尋找局部最優解題的不足和以往經驗數據引起的誤差,本發明採用高度非線性的方式,並實現給出局部最優解,大大降低了獲取最優解的複雜度,並且評估每個孩子染色體所對應個體的適應度,將孩子染色體傳入遺傳算法中,有效提高了虛擬內存大小和物理主機的適配度。
基於上述方法,具體的,對於步驟2,根據父母染色體產生多個孩子染色體的過程具體包括:獲取染色體的平均值,方差,期望,部分交叉和父母個體,產生一個孩子染色體的集合。
進一步的,步驟3中,所述評估每個孩子染色體所對應個體的適應度之後,還包括:在孩子染色體中去除不符合適應度要求的染色體。
進一步的,步驟3中,所述將孩子染色體傳入遺傳算法中之前,還包括:對孩子染色體進行交叉操作和變異操作。
其中,可以根據染色體的選擇和交叉過程修改算法來增強適應性。本方法中,包括:最優化問題表示方法、處理約束條件、初始化過程、選擇過程、災變、交叉過程、變異操作、循環操作、得到最優解。
其中,染色體的確定是:初始運行確定多個染色體(隨機確定即可),第一次運算的所產生的染色體作為選擇最優的兩條為父母染色體,然後在根據需求設置一個或多個孩子染色體傳入這次遺傳算法中,從而產生更多的孩子染色體,在將此作為下次的染色體的父母染色體,但記錄最優解,以此類推。主要分為三種確定染色體的方法:(1)爬山法。(2)模擬退火。(3)遺傳算法。
遺傳算法的局部搜索能力較強,但是很容易陷入局部極值,雖然增加變異概率可以搜索到遠離當前極值的點,但是新點的值往往不能和當前保留下來的較優值相提並論,因為這些較優值都是經過千百代的進化而存留下來的,於是遠離當前極值的點往往在兩到三代以內就被淘汰掉了。那麼如何解決遺傳算法容易陷入局部極值的問題呢?要跳出局部極值就必須殺死當前所有的優秀個體,從而讓遠離當前極值的點有充分的進化餘地,這就是災變的思想。
對於局部最優解,一般來說,最優解在每次傳入的遺傳算法的父母染色體中,也可以分析日誌得出想要的結果。
因為遺傳算法中的每一個染色體,對應著遺傳算法的一個解決方案,我們遺傳算法中還有自適應函數來判斷這個染色體的優劣,所以從一個染色體到其解的適應度形成一個映射。正好和虛擬內存測試需要大量微小差別的測試用例相適應。
基於本方法,具體實施過程包括:(1)隨機選擇多個染色體作為初始值傳入遺傳算法得到最優的兩條為父母染色體,以往經驗數據也可作為初始染色體、(2)根據父母染色體產生多個孩子染色體,比如經過取父母染色體平均值,方差,期望,部分交叉,父母個體或全部加減部分區間等方式產生一個孩子染色體的集合,這個部分也稱父母染色體變異、(3)評估每條染色體所對應個體的適應程度,首先,剔除明顯不符合要求的染色體,然後將這些染色體傳入遺傳算法中、(4)遵照適應度越高,選擇概率越大的原則,從種群中選擇兩個計算結果最優的染色體作為父方和母方,但同時記錄下所有染色體的計算數據,(5)、然後在重複(2)、(3)、(4)步。
遺傳算法的運行時間和得到最優解的結果如圖2所示,當到達一定時間後,結果將趨近於最優解,但是未到達運行時間內就是局部最優解,因為最優解有可能運行時間太長,所以只能取可以接受的部分最優解。
本發明的有益效果是:(1)現行的大多數優化算法都是基於線性、凸性、可微性等要求,而遺傳算法只需要適合度信息,不需要導數等其他輔助信息,對問題的依賴性較小,因而具有高度的非線性。(2)遺傳算法從一組初始點開始搜索,而不是從某一個單一的初始點開始搜索。而且給出的是一組優化解,而不是一個優化解,這樣可以給設計者更大的選擇餘地。(3)遺傳算法具有很強的易修改性。即使對虛擬內存大小問題進行很小的改動(比如目標函數的改進),現行的大多數算法就有可能完全不能使用,而遺傳算法則只需作很小的修改就完全可以適應新的問題。(4)將搜索過程作用在編碼後的字符串上,不直接作用在優化問題的具體變量上,在搜索中用到的是隨機的變換規則,而不是確定的規則。
遺傳算法在搜索時採用啟發式的搜索,而不是盲目的窮舉,因而具有更高所搜索效率,得出更精確的虛擬內存大小。用遺傳算法確定物理主機虛擬內存局部最優解具有上述優點,使其彌補了普通算法尋最優解的不足和以往經驗數據引起的誤差,採用高度非線性的方法,並實現給出局部最優解的方法,大大降低了此類問題的複雜度,有效提高了虛擬內存大小和物理主機的適配度,不論是在算法方面還是在虛擬內存的確定等問題都有很高的技術價值。
生物遺傳物質的主要載體是染色體,在遺傳算法中,染色體通常是一串數據(或數組),用來作為優化問題的解的代碼,其本身不一定是解。遺傳算法一般經過這樣幾個過程:首先,隨機產生一定數量的隨機染色體,這些隨機產生的染色體組成一個種群。種群中染色體的數目稱為種群大小或種群規模。然後用評價函數評價每一個染色體的優劣,即染色體對環境的適應程度(稱為適應度),用來作為以後遺傳的依據。接著進行選擇過程,選擇的目的是為了從當前種群中選出優良的染色體,使他們稱為新一代的染色體,判斷染色體優良與否的標準就是各自的適應度,即染色體的適應度越高,其被選擇的機會就越多。通過選擇過程,產生一個新的種群。對這個新的種群進行交叉操作,交叉操作是遺傳算法中主要的遺傳操作之一。接著進行變異操作,變異的操作是挖掘種群中個體的多樣性,克服有可能陷入局部解的弊病。這樣,經過上述運算產生的染色體稱為後代。然後,對新的種群(即後代)重複進行選擇、交叉和變異操作,經過給定次數的迭代處理後,把最好的染色體最為優化問題的最優解。
最優化問題表示方法:最優化問題的解有兩種表示方法:二進位向量和浮點向量。使用二進位向量作為一個染色體來表示決策變量的真實值,向量的長度依賴於要求的精度,使用二進位代碼的必要性已經受到一些批評。在求解複雜優化問題時,二進位向量表示結構有時不大方便。另一種表示方法是浮點向量,每一個染色體由一個浮點向量表示,其長度與解向量相同。這裡用x=(x1,x2,...,xn)表示最優化問題的解,其中n是維數,則相應的染色體也是V=(x1,x2,...,xn)。
處理約束條件:處理約束條件的關鍵在於(1)刪除約束條件中所有的等式,(2)設計恰當的遺傳操作以保證所有新產生的染色體在可行集中。
初始化過程:評價函數(用eval(V)來表示)用來對種群中的每個染色V設定一個概率,以使該染色體被選擇的可能性與種群中其它染色體的適應性成比例,即通過輪盤賭,適應性強的染色體被選擇產生後代的機會要大。第一種方法,設目前該代中的染色V1,V2,...,Vn,可以根據染色體的序進行再生分配,而不是根據實際的目標值。無論何種數學規劃(單目標、多目標或目標規劃)都可以作一合理假設,即在染色體V1,V2,...,Vn中,決策者可以給出一個序的關係,使染色體由好到壞進行重排,就是說,一個染色體體越好,其序號越小。設參數,定義基於序的評價函數為:i=1,2,...,n;i=1意味著染色體最好,i=n說明染色體是最差的。
第二種方法對適應度進行適當的縮放調整(稱為適應度定標)來設計評價函數。用f1,f2,...,fn(即染色體V1,V2,...,Vn各自的目標值)來表示原來的適應度。Goldberg[1]提出一種線性適應度定標方案為:i=1,2,...,n;其中為新的適應度,a和b為參數。這種方法假定使用者了解目標函數的性質,這樣才能設計合理的參數a和b。這種情況下,評價函數定義為:i=1,2,...,n。
選擇過程:選擇過程是以旋轉輪盤賭n次為基礎的。每次旋轉都為新的種群選擇一個染色體。賭輪是按照每個染色體的適應度進行選擇染色體的。無論使用哪一種評價函數,選擇函數總可以寫成如下形式:(1)對每個染色體Vi,計算累計概率qi;(2)從區間[0,qn]中產生一個隨機數r;(3)若r=qi,則選擇第i個染色體Vi,(1≤i≤n);(4)重複步驟2和步驟3共n次,這樣可以得到n個複製的染色體。在實際應用中可以將qi,i=1,2,...,n除以qn,使qn=1,新的概率同樣與適應度成正比。
災變操作:從500開始遞減,每一代遞減一次,如果出現了新的最優值,就從新開始計數,如果出現新最優值的時候倒計數遞減次數的2.5倍已經超過500則從新的初始值開始倒數。例:初始倒數500,如果倒數到200時出現新最優值,則從(500-200)2.5=750開始從新倒數,下一次如果倒數到100時出現新最優值,則從(750-100)*2.5=1625開始倒計數,這裡的2.5是一個經驗值,可以在全局參數設置裡面調整。也就是說倒計數的長度取決於進化的速度,進化速度越慢倒計數長度越長。如果倒計數完畢還沒有新的最優值,就認為局部搜索已經充分,就發生災變,剔除qi(1≤i≤5),並返回選擇過程。災變過程滿足一定條件執行。
交叉過程:首先定義Pc作為交叉操作的概率,這個概率說明種群中有期望值為Pc·n個染色體進行交叉操作。為確定交叉操作的父代,從i=1到n重複以下操作:從[0,1]中產生隨機數r,如果r<Pc,則選擇Vi作為一個父代。將選擇出來的父代隨機分成對。然後對每對進行交叉操作,例如首先產生(0,1)之間的一個隨機數c,然後按下列形式在之間進行交叉操作,並產生兩個後代X和Y。如果可行集是凸的,這種凸組合交叉運算保證兩個後代也是可行的;如果可行集不是凸集或很難驗證,這時需要對X,Y進行檢驗,如果不符合約束條件,則需重新產生c值,重複以上交叉操作。
變異操作:定義Pm作為交叉操作的概率,這個概率說明種群中有期望值為Pm·n個染色體進行交叉操作。類似交叉操作,首先選擇需要變異的父代,然後對每個需變異的父代(用V表示),用下列方法進行變異。在Rn中隨機選擇變異方向d,取M為足夠大的一個數,如果V+M·d是不可行的,則設M為0到M之間的隨機數,直到其可行為止。
循環操作:將選擇好的染色體再次傳入遺傳算法,記錄每個染色體,然後再進入上述循環操作。
得到最優解:可以設定算法運行時間,根據記錄的染色體日誌或者自適應方案選擇規定時間內的最優解。
請參考圖3,圖3為本發明所提供的一種物理主機虛擬內存分析裝置的結構示意圖,該裝置用於實現上述物理主機虛擬內存分析方法,該裝置包括:
選擇模塊101,用於隨機選擇多個染色體作為初始值輸入至遺傳算法,得到最優的兩條作為父母染色體;
其中,所述多個染色體為物理主機虛擬內存數據;
生產模塊102,用於根據父母染色體產生多個孩子染色體;
評估模塊103,用於評估每個孩子染色體所對應個體的適應度,將孩子染色體傳入遺傳算法中,從種群中選擇出最優的兩個計算結果作為新的父母染色體;
重複模塊104,用於重複調用生產模塊和評估模塊,直至獲取到最優解,將最優解作為物理主機虛擬內存局部最優解。
可見,該裝置採用遺傳算法確定物理主機虛擬內存局部最優解,彌補了普通算法尋找局部最優解題的不足和以往經驗數據引起的誤差,本發明採用高度非線性的方式,並實現給出局部最優解,大大降低了獲取最優解的複雜度,並且評估每個孩子染色體所對應個體的適應度,將孩子染色體傳入遺傳算法中,有效提高了虛擬內存大小和物理主機的適配度。
基於上述裝置,具體的,所述生產模塊具體用於獲取染色體的平均值,方差,期望,部分交叉和父母個體,產生一個孩子染色體的集合。
進一步的,所述評估模塊還包括:去除單元,用於在孩子染色體中去除不符合適應度要求的染色體。
進一步的,所述評估模塊還包括:操作單元,用於對孩子染色體進行交叉操作和變異操作。
以上對本發明所提供的一種物理主機虛擬內存分析方法及裝置進行了詳細介紹。本文中應用了具體個例對本發明的原理及實施方式進行了闡述,以上實施例的說明只是用於幫助理解本發明的方法及其核心思想。應當指出,對於本技術領域的普通技術人員來說,在不脫離本發明原理的前提下,還可以對本發明進行若干改進和修飾,這些改進和修飾也落入本發明權利要求的保護範圍內。
