一種基於視覺認知的滾動軸承變工況故障診斷方法與流程

2023-11-03 13:06:27 1

本發明涉及滾動軸承變工況故障診斷技術，特別涉及一種基於視覺認知的滾動軸承變工況故障診斷方法。

背景技術：

滾動軸承是工業中應用最為廣泛部件，滾動軸承故障可能會引起機器系統的故障，從而造成巨大的經濟損失，故障診斷是許多領域的研究熱點之一，它有助於減少組件和系統故障可能導致的損失，因此具有十分重要的意義。

在眾多的信號採集方法中，基于振動信號的測量方法由於與故障高度相關性、易獲取性和無損害性得以廣泛應用。然而，滾動軸承的工作環境通常是複雜的、惡劣的和變化的，而目前滾動軸承的故障診斷往往是假設滾動軸承工作在固定工況下來進行研究的，而這些方法對於變工況的滾動軸承診斷就無能為力了。通過文獻調研發現，在眾多的滾動軸承故障診斷中，針對變工況下的滾動軸承研究較少，其中：田野等人通過對信號進行局部均值分解(localmeandecomposition，lmd)並提取奇異值作為信號特徵進行變工況下的故障診斷，但是lmd通常會產生頻率混淆和端點效應，對診斷效果會產生很多影響；c.mishra等人利用小波降噪和角度同步平均來診斷故障軸承在變轉速下的故障，然而，小波降噪對信號的先驗知識有很大的依賴，因此也會對診斷效果產生影響。

經過多年發展，傳統的基于振動信號分析的滾動故障診斷方法主要包括以下三個步驟：(1)滾動軸承信號採集；(2)振動信號特徵提取；(3)滾動軸承故障診斷，其中第二步和第三步是故障診斷的關鍵。基於以上思路，研究學者提出了眾多的軸承信號故障特徵提取方法，如經驗模態分解(empiricalmodedecomposition,emd)、短時傅利葉變換(short-timefouriertransform，stft)、lmd和小波包分解(waveletpacketdecomposition,wpd)等，然而，emd具有過包絡、欠包絡、端點效應和頻率混淆等缺點；stft無法同時滿足解析度和時間的要求；lmd同樣也會有頻率混淆和端點效應；對於wpd，小波分解在選擇小波基時對信號的先驗知識具有極強的依賴性。考慮到在信號特徵提取時以上方法的弊端，需要研究一種新的軸承信號的特徵提取方法，來實現變工況下的滾動軸承故障診斷。

認知科學是一個跨學科研究，它涉及包括心理學、神經科學、語言學、哲學、計算機科學、人類學、社會學和生物學的各個領域。大量的學者已經研究了人類的感覺器官的認知能力，其中視覺認知已成為近年來認知科學的熱門話題，當前，視覺認知計算已經在多個領域得到應用，其中包括人臉識別、手勢識別、手寫字體識別等。從本質上講，視覺認知屬於仿生學鄰域，它是基於人類視覺系統來進行識別的，視覺認知的一個重要特點就是視覺不變性(vic)，也就是說，視覺認知可以不受所識別的物體的相對空間位置的限制來進行識別。人類視覺系統能夠對視角、形變、尺度和光照發生變化的對象識別出來。

由於基於視覺不變形提取的故障特徵維數較高，需要對其進行維數約減，以減少後續計算量。h.s.seung等人指出，大腦將圖像存儲為一個維數等於眼睛感光細胞的數量的流形，這是人類視覺系統的另一個特點—流形感知特性(mpc)，流形學習可以有效地發掘隱藏在高維數據中的低維非線性結構。

本發明將視覺不變性和流形感知特性應用於滾動軸承故障診斷，有效解決變工況條件下的滾動軸承故障診斷問題。

技術實現要素：

根據本發明實施例提供的一種基於視覺認知的滾動軸承變工況故障診斷方法，為滾動軸承變工況條件下的故障診斷提供一套新的解決思路。

根據本發明實施例提供的一種基於視覺認知的滾動軸承變工況故障診斷方法，包括：

採用遞歸圖技術將變工況下的滾動軸承振動信號轉換為二維圖像；

利用加速魯棒特徵surf算法，對所述二維圖像進行特徵提取，得到具有視覺不變性的高維故障特徵向量；

利用等距映射isomap算法，對所述高維故障特徵向量進行降維處理，得到低維穩定特徵向量；

利用奇異值分解svd算法，提取所述低維穩定特徵向量所構建特徵矩陣的奇異值，形成最終特徵向量；

利用已訓練的分類器，對所述最終特徵向量進行故障分類，對變工況下的滾動軸承進行故障診斷。

優選地，所述的採用遞歸圖技術將變工況下的滾動軸承振動信號轉換為二維圖像包括：

對滾動軸承振動信號的時間序列進行相空間重構，得到重構後的相空間矩陣，並計算重構後的相空間矩陣中兩個相點之間的距離；

利用相空間矩陣中兩個相點之間的距離，計算遞歸圖中的遞歸值，並利用所述遞歸值，繪製遞歸圖作為二維圖像。

優選地，所述的利用surf算法，對所述二維圖像進行特徵提取，得到具有視覺不變性的高維故障特徵向量包括：

通過採用不同尺度的盒子濾波器對所述二維圖像進行處理，構建尺度空間金字塔，並在所述尺度空間金字塔中檢測出局部極值點；

對所述局部極值點進行篩選處理，並將篩選得到的局部極值點作為興趣點；

基於所述興趣點進行插值處理，並將插值得到的興趣點作為關鍵點；

對每個關鍵點進行方向分配及特徵描述處理，得到由每個關鍵點的特徵描述數據構成的高維故障特徵向量。

優選地，所述的利用isomap算法，對所述高維故障特徵向量進行降維處理，得到低維穩定特徵向量包括：

利用所述高維故障特徵向量中每個關鍵點與其他關鍵點之間的歐氏距離，確定每個關鍵點的鄰域內的關鍵點和鄰域外的關鍵點；

根據每個關鍵點的鄰域內的關鍵點和鄰域外的關鍵點，計算每個關鍵點與其他關鍵點之間的最短距離；

利用每個關鍵點與其他關鍵點之間的最短距離，構建最短路徑距離矩陣；

利用mds算法，對所述最短路徑距離矩陣進行處理，得到約減後的特徵矩陣，並利用約減後特徵矩陣的特徵值和特徵向量，構建低維穩定特徵向量；

其中，所述樣本點是關鍵點的特徵描述數據。

優選地，所述高維故障特徵向量的維度為64，所述低維穩定特徵向量和所述最終特徵向量的維度在2至30之間。

本發明實施例提供的技術方案具有如下有益效果：

1、本發明實施例將視覺認知領域中的方法引入滾動軸承變工況故障診斷領域，為滾動軸承故障診斷提供了一種新的解決思路；

2、本發明實施例基於遞歸圖技術，將變工況下的滾動軸承振動信號轉化成為二維圖像，該方法適用於非線性、非平穩信號，為基於視覺不變性的故障特徵提取提供了圖像基礎；

3、本發明實施例基於人類視覺系統具有視覺不變性的特點，採用surf算法提取所轉換二維圖像的穩定故障特徵，從而可有效解決變工況條件下的滾動軸承故障診斷問題；

4、本發明實施例基於流形感知特性，採用isomap算法構建低維本質流形，對基於視覺不變性提取的故障特徵進行維度約減，可去除冗餘故障特徵，大大減少計算量，提高計算速度。

5、本發明實施例提出的是一套基於遞歸圖圖像等效表徵、surf穩定故障特徵提取和isomap流形降維的一整套滾動軸承變工況故障診斷方法，可有效實現滾動軸承變工況工作條件下的故障分類，具有很高的故障診斷精度。

附圖說明

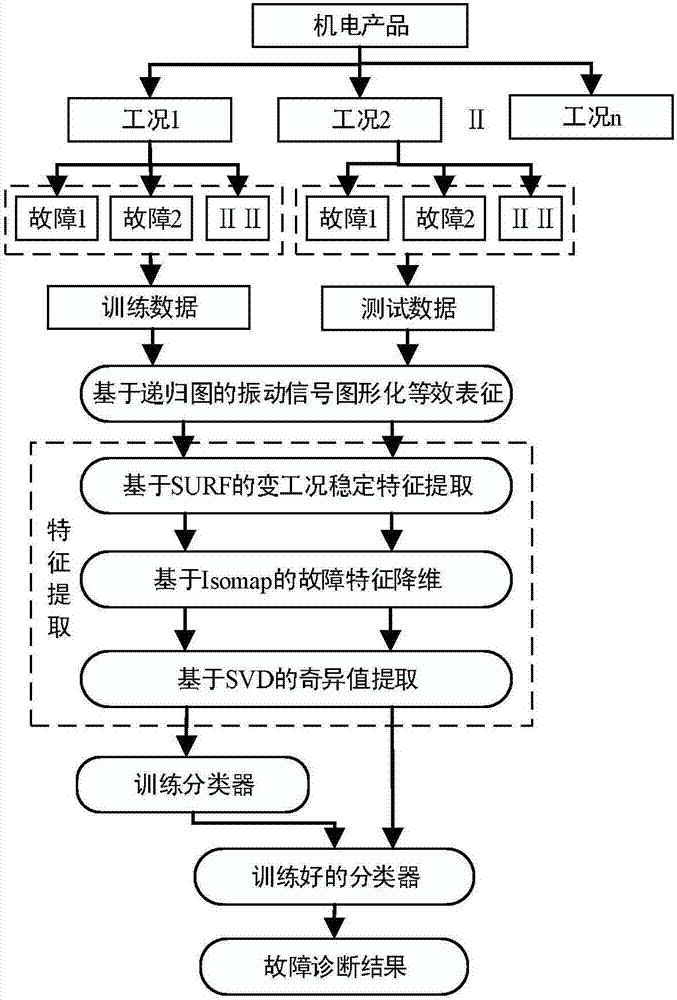
圖1是本發明實施例提供的基於視覺認知的滾動軸承變工況故障診斷方法框圖；

圖2是本發明實施例提供的基於視覺認知的滾動軸承變工況故障診斷方法原理圖；

圖3(a)至3(d)分別是原始圖像，及其平移、旋轉和尺度的變化圖；

圖4是相同圖像的亮度變化圖；

圖5是積分圖像的功能示意圖；

圖6是盒式濾波器用於近似二階高斯偏導數的示意圖；

圖7是尺度金字塔示意圖；

圖8是興趣點的定位示意圖；

圖9是離散和連續空間的區別示意圖；

圖10是關鍵點的方向分布示意圖；

圖11是surf特徵描述符生成示意圖；

圖12(a)至圖12(c)是swissroll中的測地距離示意圖；

圖13是滾動軸承數據採集試驗臺；

圖14是不同工況下不同故障模式所轉化的遞歸圖；

圖15是surf所檢測的圖14所示遞歸圖中的關鍵點示意圖；

圖16是二維空間的特徵散點圖；

圖17是三維空間的特徵散點圖。

具體實施方式

以下結合附圖對本發明的優選實施例進行詳細說明，應當理解，以下所說明的優選實施例僅用於說明和解釋本發明，並不用於限定本發明。

圖1是本發明實施例提供的基於視覺認知的滾動軸承變工況故障診斷方法框圖，如圖1所示，包括以下步驟：

採用遞歸圖技術將變工況下的滾動軸承振動信號轉換為二維圖像；

利用加速魯棒特徵surf算法，對所述二維圖像進行特徵提取，得到具有視覺不變性的高維故障特徵向量；

利用等距映射isomap算法，對所述高維故障特徵向量進行降維處理，得到低維穩定特徵向量；

利用所述低維穩定特徵向量，構建特徵矩陣，並利用svd算法，提取所構建特徵矩陣的奇異值，利用所提取的奇異值，構建最終特徵向量；

利用已訓練的分類器，對所述最終特徵向量進行故障分類，對變工況下的滾動軸承進行故障診斷。

上述的採用遞歸圖技術將變工況下的滾動軸承振動信號轉換為二維圖像包括：對滾動軸承振動信號的時間序列進行相空間重構，得到重構後的相空間矩陣，並計算重構後的相空間矩陣中兩個相點之間的距離；利用相空間矩陣中兩個相點之間的距離，計算遞歸圖中的遞歸值，並利用所述遞歸值，繪製遞歸圖作為二維圖像。

上述的利用surf算法，對所述二維圖像進行特徵提取，得到具有視覺不變性的高維故障特徵向量包括：通過採用不同尺度的盒子濾波器對所述二維圖像進行處理，構建尺度空間金字塔，並在所述尺度空間金字塔中檢測出局部極值點；對所述局部極值點進行篩選處理，並將篩選得到的局部極值點作為興趣點；基於所述興趣點進行插值處理，並將插值得到的興趣點作為關鍵點；對每個關鍵點進行方向分配及特徵描述處理，得到由每個關鍵點的特徵描述數據構成的高維故障特徵向量。也就是說，本發明將變工況下的滾動軸承振動信號轉化成為二維圖像後，利用人類視覺系統的視覺不變性的特點來提取所轉換圖像的穩定特徵，從而實現變工況下的穩定故障特徵提取

上述的對所述局部極值點進行篩選處理，並將篩選得到的局部極值點作為興趣點包括：對所述尺度空間金字塔中每個像素點與其同一尺度圖像內的多個鄰近像素點及上一尺度和下一尺度圖像內的多個鄰近像素點的灰度值進行比較；若比較結果為該像素點的灰度值大於或小於所述所有鄰近像素點的灰度值，則確定該像素點為興趣點。

在一個具體實施例中，所述的對所述局部極值點進行篩選處理，並將篩選得到的局部極值點作為興趣點包括：對所述尺度空間金字塔中每個像素點與其同一尺度圖像內的8個鄰近像素點及上一尺度和下一尺度圖像內的各9個鄰近像素點的灰度值進行比較；若比較結果為該像素點的灰度值大於或小於所有26個鄰近像素點的灰度值，則確定該像素點為興趣點。

上述的對每個關鍵點進行方向分配及特徵描述處理，得到所述高維故障特徵向量包括：利用haar小波響應值和主方向描述每個關鍵點，生成具有旋轉不變性的surf特徵描述子作為高維故障特徵向量。

上述的所述的利用isomap算法，對所述高維故障特徵向量進行降維處理，得到低維穩定特徵向量包括：利用所述高維故障特徵向量中每個樣本點與其他樣本點之間的歐氏距離，確定每個樣本點的鄰域；計算每個樣本點與其鄰域內其他樣本點之間的最短距離，構建最短路徑距離矩陣；利用mds算法，對所述最短路徑距離矩陣進行處理，得到約減後的特徵矩陣，並利用約減後特徵矩陣的特徵值和特徵向量，構建低維穩定特徵向量；其中，所述樣本點是關鍵點的特徵描述數據。也就是說，本發明使用流形學習來構建低維本質流形從而對視覺不變性提取的故障特徵進行維度約減。

上述的根據每個關鍵點的鄰域內的關鍵點和鄰域外的關鍵點，計算每個關鍵點與其他關鍵點之間的最短距離包括：將每個關鍵點與其鄰域內的關鍵點之間的歐式距離作為該關鍵點與其鄰域內的關鍵點之間的最短距離；利用dijkstra算法或folyd算法，計算每個關鍵點與其鄰域外的關鍵點之間的流形上的最短距離。

本發明通過預先使用已知狀態數據的最終特徵向量對分類器進行訓練，得到已訓練的分類器，具體包括：利用同一工況下的已知狀態數據經過前述處理得到已知狀態數據的最終特徵向量；將所述已知狀態數據的最終特徵向量送入分類器進行訓練，得到已訓練的分類器。所述分類器可以是支持向量機svm分類器，也可以是概率神經網絡pnn分類器等，也就是說，本發明可採用svm分類器或pnn分類器等實現滾動軸承的故障診斷。

在一個具體實施例中，所述高維故障特徵向量的維度為64維，低維穩定特徵向量和所述最終特徵向量的維度在2至20之間。

下面以具體實施例對本發明做出進一步說明，需要指出的是，以下說明僅僅用於解釋本發明的上述方法，而不是用來限定本發明的上述方法。

圖2是本發明實施例提供的基於視覺認知的滾動軸承變工況故障診斷方法原理圖，如圖2所示，本發明的故障診斷方法主要包括以下步驟：基於遞歸圖的圖像轉換，基於surf算法、isomap算法和svd算法的特徵提取以及故障分類。具體地說，首先採用遞歸圖技術將不同工況下的滾動軸承振動信號轉換為二維圖像。然後，針對二維圖像應用surf算法提取穩定故障特徵向量，得到64維特徵矩陣，進而利用isomap算法對該特徵矩陣進行降維，得到低維穩定特徵向量，並利用svd算法提取低維穩定特徵向量所構建的特徵矩陣的奇異值，形成最終特徵向量。最後，在不同工況下，分別選取部分最終特徵向量作為訓練數據訓練分類器，將剩餘最終特徵向量作為測試數據送入已訓練好的分類器實現故障分類。

1、具體實施例如下：

1.1基於遞歸圖的圖像轉換

將視覺認知理論引入滾動軸承故障診斷領域的首要工作是實現一維振動信號向二維圖像信號的轉變。圖像轉換是確保使用vic特徵提取成功的一個重要基礎，因此，選擇合適的圖像變換方法極其重要。考慮到滾動軸承信號的非線性和不穩定性，複雜系統動態變化的檢測是最困難的問題之一。

遞歸圖是一種在二維平面上對重構相空間中的動力學軌道遞歸行為進行刻畫的一種方法。它是一個在時間平面內由黑點和白點構成的二維平面圖，黑點表示在時間序列的這個點上存在遞歸行為，白點表示沒有遞歸。

本實施例採用遞歸圖技術將不同工況下的滾動軸承振動信號轉換為二維圖像，為後續特徵提取提供基礎。遞歸圖技術的具體實現步驟如下：

(1)對於採樣時間間隔為δt的時間序列uk＝(k＝1,2,…,n)，採用cao法及互信息法選擇合適的嵌入維數m及延遲時間τ重構時間序列，重構後的動力系統為xi＝(ui,ui+τ,…,ui+(m-1)τ)i＝1,2,…,n-(m-1)τ。

(2)計算重構後的相空間中第i點xi和第j點xj的距離sij，如下：

sij＝||xi-xj||,i＝1,2,…,n-(m-1)τ；j＝1,2,…,n-(m-1)τ

(3)計算遞歸值：r(i,j)＝h(εi-sij)i＝1,2,…,n-(m-1)τ，其中，εi為截止距離，可取固定值或隨i改變，使得半徑為εi的球包含一定的鄰域數。式中h(r)為heaviside單位函數：

(4)繪製遞歸圖。將r(i,j)在以i為橫坐標，j為縱坐標的坐標圖上繪製出來，得到遞歸圖。r(i,j)的值為0或1，分別代表圖中的白點和黑點。其中i與j分別為時間序列標號i與j，所得到的圖為遞歸圖。由r(i,j)＝r(j,i)和r(i,j)＝1,(i＝j)可知，遞歸圖中存在一條主對角線，遞歸圖關於主對角線是對稱的。

1.2基於視覺不變性的穩定故障特徵提取

圖像轉換之後，利用surf算法從二維圖像中提取特徵。

1.2.1視覺不變性理論

人類視覺系統(hvs)是人類感知外部世界最直觀的工具，最近其在圖像處理領域獲得極大關注。視覺不變性(vic)理論的主要思想是：(1)圖像由邊緣和紋理等細節組成；(2)不變量是對象的幾何結構的基本描述。由於不變量在對象的識別中起關鍵作用，所以它是視覺對象中最重要的幾何結構。

人類通過視覺感知外部世界是基於提取不變的特徵，也就是說人眼對外部對象的識別是不隨著對象的旋轉、縮放、平移和亮度變化的。圖3(a)至3(d)分別是原始圖像，及其平移、旋轉和尺度的變化圖，圖4是相同圖像的亮度變化圖，如圖3和圖4所示，這是hvs的最重要的特徵。這表示人眼基於對象本身的特性信息識別和理解對象，並且這不隨旋轉或縮放而改變。正是由於人類的視覺捕捉了同一個目標的不變量，人們才能識別物體。

由於在相同故障模式的變工況條件下滾動軸承可以顯示類似的圖像特徵，所以本發明選擇圖像轉換方法並且採用hvs的vic來提取在不同條件下相同故障模式的不變特徵。

1.2.2加速魯棒特徵

對發生旋轉、縮放、平移等變化的圖像進行識別也就是尋找圖像中的穩定點，這些點如角點、斑點、暗區中的亮點和亮區中的暗點是不隨圖像的旋轉、縮放、平移發生變化的。尺度不變特徵變換(sift)是視覺不變性理論的計算方法，它可以識別圖像中不變的特徵從而實現圖像匹配。後來，對sift進行改進後提出一種新的方法，即加速魯棒特徵(surf)。相對於sift，surf由於其計算的快速性、魯棒性和可重複性使得其廣泛應用。

(1)尺度空間理論

尺度空間的基本理論是將尺度參數引入到圖形中，並且通過連續改變尺度參數來獲得多尺度下的尺度空間。然後提取不同尺度下的圖像的角點和邊緣作為特徵向量，以實現檢測。

(2)積分圖像

由於積分圖像可以大幅提高方框狀卷積濾波器的運算效率，因此提高了surf算法的運算速度。積分圖像iσ中的任意一點(x,y)的值iσ(x,y)由計算得出，它代表由原圖像原點和點(x,y)構成的矩形區域內所包含的所有像素之和。其中，iσ(x,y)為iσ在(x,y)處的積分圖像值；i(i,j)為原圖像的灰度值。iσ(x,y)可以由公式s(x,y)＝s(x,y-1)+i(x,y)和公式iσ(x,y)＝iσ(x-1,y)+s(x,y)迭代運算得到。s(x,y)表示圖像在i在x列的積分，且有s(x,-1)＝0，iσ(-1,y)＝0。

由上式可以看出通過簡單重複性的加減運算即可求出矩形區域內像素點的和，採用這種思路可以大大提高程序的運算效率。圖5是積分圖像的功能示意圖，如圖5所示，積分圖像中矩形區域內的灰度值之和可以通過3個加減運算來實現，即σ＝iσ(a)-iσ(b)-iσ(c)+iσ(d)，與窗口w的大小無關。從後面的介紹中可以得知，surf算法中所使用的卷積模板均為框狀模板，這就大大提高了運算效率。

(3)關鍵點的定位

步驟1：建立尺度空間金字塔。通過採用不同尺度的盒子濾波器對所述二維圖像進行處理，構建尺度空間金字塔。

surf利用行列式的近似hessian矩陣的局部極大值來定位關鍵點。當hessian矩陣的行列式是局部極大值時，檢測到的點就是關鍵點。在初始圖像上的點x(x,y)處，具有尺度σ的hessian矩陣h(x,σ)定義如下：其中，lxx(x,σ)是高斯二階導數和圖像i在點x處的卷積，lxy(x,σ)和lyy(x,σ)同理。

使用盒子濾波去近似高斯的二階偏導，再與原圖像做卷積，並在這一過程中使用積分圖像進行計算，大大提高了其運算效率。圖6是盒式濾波器用於近似二階高斯偏導數的示意圖，如圖6所示，通過積分圖像可以快速得到盒子濾波器。計算量與模板大小無關，從而提高了surf的計算效率。

當使用以9×9的盒子濾波器近似σ＝1.2的高斯二階偏導濾波器時，hessian矩陣的行列式為det(h)＝lxxlyy-lxylxy，簡化後，矩陣變為det(happrox)＝dxxdyy-(0.9dxy)2。

為了實現關鍵點的尺度不變性，surf在原始圖像上使用不同尺度的盒子濾波器，從而獲得尺度金字塔，如圖7所示。surf算法中所構建的尺度空間也包括若干組圖像，每組圖像又包含若干層。這些圖像都是通過與不斷增大的盒子濾波器進行卷積得到的。為了使得濾波模板中的方塊按照整數個像素放大，下一層的盒子濾波器尺度要在上一層的基礎上進行翻倍。假如選取6作為基本尺度間隔，將上述9×9的濾波器作為第一組的初始濾波模板，則第一組盒子濾波器的模板尺寸依次為：9×9，15×15，21×21，27×27。第二組類似，只是相鄰的兩個濾波器的尺度間隔為12，這個差值是第一組的兩倍，即15×15，27×27，39×39，51×51。第三組，第四組類似。每層對應的尺度值為：其中，n為模板的邊長。

步驟2：局部極值點檢測。在步驟1構建的尺度空間金字塔中檢測出局部極值點。

尺度空間金字塔構建完成後，需要在尺度空間內進行極值點檢測。surf算法通過檢驗近似hessian矩陣行列式的值實現極值點檢測。若行列式的值為正，則可確定該點為局部極值點。

步驟3：興趣點篩選。對所述局部極值點進行篩選處理，並將篩選得到的局部極值點作為興趣點。

在得到局部極值後，需要將其與3×3×3立體鄰域內的像素值進行比較，只有比與其同尺度鄰近的8個像素點以及上下鄰近尺度各9個點共26個點都大或都小的極值點才被選為關鍵點，如圖8所示。

步驟4：關鍵點定位。基於所述興趣點進行插值處理，並將插值得到的興趣點作為關鍵點。

離散空間中的極值點並不是真正的極值點，圖9描述了離散空間和連續空間中的二次函數極值點的差異，surf利用線性插值的方法獲得準確的關鍵點。

步驟5：關鍵點描述。對每個關鍵點進行方向分配及特徵描述處理，得到所述高維故障特徵向量。

為了確保旋轉不變性，需要對檢測到的關鍵點確定其主方向。首先計算關鍵點周圍一個半徑為6σ的圓形區域的x和y方向的haar小波響應，其中σ是被檢測關鍵點的尺度。然後以關鍵點為中心，以圓心角為60°扇形的窗口掃描該圓形區域，每掃描1°計算扇形覆蓋的區域內haar小波響應的累加和，形成一個矢量。扇形掃描一周便可以得到360個矢量。其中長度最大的矢量對應的角度即為特徵點主方向，如圖10所示。

以興趣點為中心，構建一個邊長為20s的正方形鄰域，其中s為該特徵點對應的尺度。為保證surf特徵描述子具有旋轉不變性，將坐標軸旋轉到上一節確定的特徵點主方向。然後將該正方形區域劃分為邊長為5s的4×4的子區域。對於每一個子區域，使用尺寸為2s×2s的haar小波模板進行處理。設dx和dy分別表示水平方向和垂直方向子區域的haar小波響應值。對所有得到的dx和dy，以特徵點為中心，使用標準差為σ＝3.3s的高斯函數進行加權運算，以增加surf特徵對幾何變形和定位錯誤情況的魯棒性。

圖11是surf特徵描述符生成示意圖，如圖11所示，左邊大的方框分為4×4＝16塊，其中每一塊又分成4個小塊，如右圖所示。對於右圖表示的子域，分別計算以下四個量：σdx，σ|dx|，σdy，σ|dy|，這樣就可以用一個4維向量v＝(σdx,σ|dx|,σdy,σ|dy|)表示右圖所示子域。將4×4＝16個子域的特徵向量連接起來，便得到了4×4×4＝64維的向量。最後，對該64維向量進行歸一化處理，便生成了對於一個特徵點的surf特徵描述符。

surf算法通常從圖像提取到數目龐大的特徵，因此巨大的計算消耗限制了其在故障診斷中的應用。為解決這一問題，需要一個降維方法來減少計算量。本發明利用isomap來降低surf特徵向量的維數。降維完成後，構建最終的特徵向量，完成特徵提取過程。

1.3基於視覺流形感知特性的故障特徵降維

1.3.1流形感知特性和流形學習

根據流形感知(manifoldperceptioncharacteristic，mpc)理論，視覺感知過程以流形拓撲連續性為基礎，當尺度、位置、光照和其它因素不斷變化時，同一物體的圖像將位於一個高維觀測空間的低維流形上。而且，hvs是通過視覺細胞接收圖像的，每個視覺細胞接收到的信息儲於多維流形空間上；然而，大腦只接受位於部分低維流形上的信息。也就是說，hvs有能力感知在高維流形中潛藏的信息。流形學習能夠發現隱藏在高維觀測空間的有意義的低維結構，並且這個概念已經吸引了越來越多的研究。受mpc的啟發，當處理由vic提取的特徵時，可以運用流形學習方法來發現流形的本質特徵。

流形學習是非線性降維法的最重要部分，已經吸引了廣泛的關注，這種方法能夠通過保留一些局部或全部的幾何結構將高維樣本嵌入到低維特徵空間中。近年來，已經提出許多流形學習方法，包括等距映射(isomap)，局部線性嵌入(lle)，拉普拉斯特徵映射(le)和局部切線空間排列(ltsa)。isomap是本文用於剩餘全球化特徵的方法。

1.3.2isomap理論

isomap是一種全局的非線性流形降維方法，它是在多維尺度變換mds的基礎上發展而來的。mds中採用歐式距離作為數據點中的度量方式，而isomap採用流形上的測地距離進行數據點之間的距離度量，從而能夠保留觀測數據集的非線性幾何結構。isomap算法假設鄰域關係圖中邊的長度可以有效表達低維空間中的局部測度信息，數據點之間的全局測度結構可通過鄰域關係圖上的最短路徑進行估計。

mds是一種傳統的能夠保持數據點之間差異性的降維方法。它可以使得數據點在映射前後數據集點對之間的距離保持不變。mds算法基於全局線性假設，其基本思想是：通過計算給定數據集樣本點之間的歐氏距離，構造數據點之間的關係矩陣，對該關係矩陣做特徵分解得到每一樣本點相應的低維坐標，從而使得變換前後點對之間的距離保持不變。mds算法的步驟如下：

(1)對於數據集x＝{xi|i＝1,2,…,n,xi∈rd}，計算任意兩點i,j之間的歐式距離dx(i,j)，構建n階平方歐式距離矩陣di,j＝dx(i,j)。

(2)將矩陣d進行雙中心化計算，即計算其中h＝i-eet/n，e＝[1,1,…,1]t。

(3)計算數據點的低維坐標y，即將矩陣τ進行奇異值分解。設λ＝[s1,s2,…,sd]為τ的最大的d個特徵值，u＝[v1,v2,…,vd]為相應的特徵向量，則最佳d維嵌入坐標為

通過mds方法採用傳統的歐式距離度量，這樣構造的距離矩陣僅能反映數據點之間的線性關係，對於非線性關係則無能為力。為了克服這一缺點，isomap算法通過引入流形空間中的測地線距離代替歐式距離來保持數據集的本質結構特徵不變。

isomap算法中採用的測地線距離可用swissroll進行說明，如圖12所示。其中圖12(a)中虛線代表兩樣本點之間的歐式距離，然而，這一距離並不能真實反映兩樣本之間的「實際」距離，圖中實線代表的測地線距離更能對處於流形空間中的兩點距離進行真實反映。圖12(b)中的實線為通過最短路徑算法計算的這兩個樣本點之間的近似測地線距離，從圖12(c)所示的二維空間分布中可以看出，下方的實線表示的近似測地線距離可以很好地逼近上方實線表示的兩點實際距離。

在isomap中，採用如下方法近似計算實際測地線距離：對於數據集中的一個樣本點，其鄰域內的測地線距離採用歐氏距離代替；其鄰域外的測地線距離用流形上的最短路徑代替。該最短路徑可採用dijkstra算法或folyd算法計算。isomap算法主要步驟如下：

(1)構造域關係圖g(v,e)

對於數據集中的每一個樣本點xi(i＝1,2,…,n)，計算其和其他樣本點之間的歐式距離。當xj為離xi最近的k個點中的一個時，或當xj與xi之間的歐式距離d(xi,xj)小於某一固定值ε時，認為圖g有邊xixj，邊xixj的權值為d(xi,xj)。

其中，所述樣本點是關鍵點的特徵描述數據。

(2)計算最短路徑

當圖g有邊xixj時，設最短路徑dg(xi,xj)＝d(xixj)；否則dg(xi,xj)＝∞，對l＝1,2,…,n，有dg(xi,xj)＝min{dg(xi,xj),dg(xi,xl)+dg(xl,xj)}，這樣便可以得到最短路徑距離矩陣

(3)計算低維嵌入

在距離矩陣dg中引入mds方法，構建d維嵌入空間y。通過最小化以下誤差方程得到坐標向量yi：其中矩陣變換算子h為集中矩陣s為平方距離矩陣

假設λ1,λ2,…,λd為h的最大的d個特徵值，其對應的特徵向量u1,u2,…,ud構成矩陣u＝[u1,u2,…,ud]，則即為d維嵌入結果。

也就是說，利用等距映射isomap算法，對所述高維故障特徵向量進行降維處理，得到低維穩定特徵向量。具體地說，首先利用所述高維故障特徵向量中每個關鍵點與其他關鍵點之間的歐氏距離，確定每個關鍵點的鄰域內的關鍵點和鄰域外的關鍵點；然後根據每個關鍵點的鄰域內的關鍵點和鄰域外的關鍵點，計算每個關鍵點與其他關鍵點之間的最短距離，例如，對於鄰域內的關鍵點，將每個關鍵點與其鄰域內的關鍵點之間的歐式距離作為該關鍵點與其鄰域內的關鍵點之間的最短距離，對於鄰域外的關鍵點，利用dijkstra算法或folyd算法，計算每個關鍵點與其鄰域外的關鍵點之間的流形上的最短距離；最後利用每個關鍵點與其他關鍵點之間的最短距離，構建最短路徑距離矩陣，利用mds算法，對所述最短路徑距離矩陣進行處理，得到約減後的特徵矩陣，並利用約減後特徵矩陣的特徵值和特徵向量，構建低維穩定特徵向量。

1.4.構建用於故障分類的最終特徵向量。

對於一幅圖像，可用surf算法檢測出多個關鍵點。對每個關鍵點進行描述，可得到一個64維的surf特徵向量，進而用isomap算法進行特徵降維，可得到一個低維穩定特徵向量。由於一幅圖像中包含多個關鍵點，因此利用surf算法及isomap算法進行特徵提取之後，可以得到對應於多個關鍵點的多個低維穩定特徵向量，進而由所述多個低維穩定特徵向量構建出一個低維特徵向量矩陣(即特徵矩陣)。然而，該低維特徵向量矩陣需轉化為一列特徵向量，才能作為後續分類器的輸入，因此本發明利用svd算法，提取所述低維特徵向量矩陣的奇異值，並由所提取的奇異值構建最終特徵向量。這樣，對於一幅圖像可得到一列最終特徵向量，該向量由奇異值組成，方便作為後續分類器的輸入，同時，進一步降低了故障特徵的維度，減少了計算量。

1.5.故障分類

本發明採用的分類器可以是svm分類器，也可以是pnn分類器等，本實施例以svm分類器為例進行說明。

在特徵提取完成以後，訓練svm分類器實現故障分類。svm分類器的輸入樣本是滾動軸承在每種工況下提取到的正常、內環故障、外環故障和滾動體故障四種模式的最終特徵向量，這些特徵向量分別被標記為1、2、3、4。然後，訓練一個4分類的svm分類器用於故障分類。

對於不同工況條件下的測試振動信號，首先將其轉換為遞歸圖，然後採用surf算法進行故障特徵提取，基於isomap進行故障特徵約減、基於svd算法提取奇異值並構建最終特徵向量。最後，將這些最終特徵向量送入訓練好的svm分類器進行分類，通過比較預測標籤和訓練標籤，計算出分類準確度。

2、實驗結果如下：

結合圖2可知，本發明通過以下四個步驟來進行變工況下的滾動軸承故障診斷：首先，將不同工況下不同故障模式的滾動軸承振動數據轉換成為rp，然後通過surf提取rp中的關鍵點，並生成故障特徵描述符。由於故障特徵是嵌入在高維流形中，因此本發明利用isomap發掘嵌入在高維流形中的低維本質流形，然後利用同一工況下的不同故障特徵訓練svm分類器，最後對變工況下的滾動軸承進行故障診斷，並且進行交叉驗證。

2.1試驗數據

為驗證本發明方法的有效性，本實施例以美國凱斯西儲大學滾動軸承數據為例，對基於加速魯棒特徵與等距映射的變工況故障診斷方法進行驗證。軸承試驗裝置如圖13所示。該試驗平臺由一個2馬力的電機(左側)(1hp＝746w)，一個轉矩傳感器(中間)，一個功率計(右側)和電子控制設備組成。軸承故障採用電火花加工技術進行注入，所注入故障直徑分別為0.007、0.014、0.021、0.028、0.040英寸。加速度傳感器通過使用磁性底座安放在電機殼體上，其所產生的振動信號由16通道dat記錄器進行採集，並且後期在matlab環境中處理。數位訊號的採樣頻率為12000hz，驅動端軸承故障數據採樣頻率為48000hz。軸承外圈故障布置在3點鐘、6點鐘和12點鐘方向。

本發明選取驅動端skf軸承為研究對象，點蝕故障直徑為0.021英寸，驅動端軸承振動數據採樣頻率為48000hz。保持電機負載及轉速不變，可得到不同工況下的驅動端軸承正常、內環故障、滾動體故障和外環故障數據。本發明選取4種工況下的軸承試驗數據進行分析，數據組成如表1所示。利用以下試驗數據，驗證基於加速魯棒特徵與等距映射的變工況故障診斷方法的可行性。

表1.試驗軸承數據信息

2.2基於遞歸圖的圖像轉換

採用遞歸圖分別對軸承4種不同工況下的正常、內環故障、外環故障及滾動體故障振動數據進行圖形化等效表徵。為了驗證在變工況條件下滾動軸承故障診斷，使用了4.8khz採樣率和4種不同轉速下的0.021英寸的振動數據。首先將不同工況下的不同故障模式的滾動軸承振動數據進行圖形化等效表徵，採用cao方法和互信息法選取合適的嵌入維數m和延遲時間τ對振動信號時間序列進行相空間重構，各工況下計算得到的參數m和τ如表2所示。在重構相空間內分析振動信號的遞歸行為，生成遞歸圖，從而實現軸承振動信號的圖形化等效表徵。為了分析工況變化對遞歸圖的影響，針對4種工況下的每種故障模式，隨機選取一組試驗數據生成遞歸圖進行對比分析，如圖14所示。

表2.不同工況下每種故障模式的實驗參數

從圖14可以看出，不同故障模式下的軸承振動信號遞歸圖具有不同的結構特徵，同種故障模式之間的振動信號遞歸圖具有很強的相似結構。受工況變化的影響，不同工況下的遞歸圖呈現出平移變化、縮放變化和、亮度變化，或這幾種變化的組合。滾動軸承的振動信號是包含在滾動軸承重要信息中最容易獲得的信號之一。選擇適當的信號處理方法可以獲得所需的特徵並且有助於故障診斷。為了探索在不同工況條件下的滾動軸承故障診斷，本發明將以上滾動軸承監測的振動信號所轉化的rp進行分析。如前所述，rp可以發現復現域中信號的隱藏周期性，這種周期性不容易發現。並且重要的是，該方法分析了時間序列的周期性，混沌和非穩定元素，因此，rp非常適合于振動信號的圖像變換，並且不會損失信號信息。

由於需要計算重構相空間裡xi和xj的歐氏距離和計算機計算速度的限制，每次僅選取1000個振動信號的振動點並將其轉換成rp，並且轉換的rp是n×n維的黑白圖像(不同條件下不同故障模式的大小顯示了非常微小的差異)。

2.3基於surf和isomap的故障特徵提取

針對上述生成的試驗軸承不同工況條件下不同故障模式的遞歸圖，採用surf算法提取滾動軸承變工況下不同故障模式下的遞歸圖的視覺不變特徵。圖15為圖14所示試驗軸承4種不同工況條件下每種故障模式的遞歸圖中檢測到的關鍵點，通過對所提取的關鍵點進行描述，建立一個4×4×4＝64維的向量描述符，也就是說，經surf進行特徵提取後，每幅遞歸圖會產生一個64維的surf視覺不變特徵向量。

考慮到surf特徵維數過高isomap方法來降低特徵矩陣的維數。本發明採用isomap算法對surf特徵向量進行約減，構建低維流形空間，為了探索分類精度和所降維度的關係，本發明將64維的高維特徵分別約減為2維、3維、5維、8維、10維、12維、15維、18維和20維，然後根據最終診斷結果確定最佳維度。

由於視覺信息出現在本質流形(intrinsicmanifold)上，本質流形嵌入在由高維流形描述的高維空間rm上，採用上述isomap方法來進行維數約減。給定rm中的任意點，代表內部岐管故障模式相應數據點能夠通過映射g＝f-1描述。然而，低維本質流形的特徵同樣太大，太複雜而不能作為特徵向量。為了解決這個問題並且提高特徵向量的魯棒性，本發明利用奇異值分解(svd)來壓縮故障特徵向量的大小，獲得更加穩定的特徵向量。因此，從高維空間到低維流形的映射g＝f-1能夠提供一個svd散點圖，該散點圖可以通過選擇第一個三維空間在三維空間中顯示。

2.4基於svm的故障分類

在降維工作完成之後，採用svm作為故障診斷分類器，實現變工況條件下的滾動軸承故障識別。為了驗證所提方法的準確性，故障診斷採用交叉檢驗的方式，將4種運行工況下採集的試驗數據依次選取其中1種工況數據作為訓練數據，其餘3種工況數據作為測試數據進行故障識別。數據組成情況如表3所示。

表3.軸承變工況故障診斷交叉檢驗數據組成.

其中，1，2，3，4在訓練數據和測試數據的條件下分別表示4種不同的速度條件，分別為1797rpm，1772rpm，1750rpm和1730rpm。

每組交叉檢驗中，訓練數據和測試數據包含的數據組數如下：

訓練數據：4種狀態模式(正常、內環故障、滾動體故障、外環故障)各選取20組數據；

測試數據：每種工況下，4種狀態模式(正常、內環故障、滾動體故障、外環故障)各選取20組數據，其中1～80組為第1種工況下的測試數據，81～160組為第2種工況下的測試數據，161～240組為第3種工況下的測試數據。

表4.不同維度下的交叉驗證準確率

表4為統計的不同約減維度下的交叉驗證的準確率，從表4中可以看出，故障診斷精度隨著維度的增加而增加，當維數達到8時，故障診斷準確率達到最高。為了在可視條件下對不同工況下不同故障模式特徵進行表示，圖16和圖17分別為2維和3維的故障特徵散點圖，從圖中可以看出，經過本發明所述方法計算之後，同一故障模式不同工況下的故障特徵表現出了很好的聚類性，而不同故障模式之間的故障特徵的可分性很好。

本發明實施例提出的一種基於視覺認知的滾動軸承變工況故障診斷方法包括以下步驟：首先，將振動信號數據轉換成為二維遞歸圖；受人類視覺系統的視覺不變性的啟發，利用加速魯棒特徵來提取所轉化的二維遞歸圖的特徵並得到對旋轉、縮放和尺度變化都不產生變化的64維特徵向量；基於人類視覺系統的流形感知特性，利用等距離映射的方法獲取高維空間中所嵌入的低維本質流形以達到維度約減的目的；最後，利用傳統的支持向量機作為分類器進行故障診斷。本發明使用美國西儲大學軸承中心的數據進行試驗，試驗結果表明本發明所提供的基於視覺認知的滾動軸承變工況故障診斷方法能夠得到很好的結果。

儘管上文對本發明進行了詳細說明，但是本發明不限於此，本技術領域技術人員可以根據本發明的原理進行各種修改。因此，凡按照本發明原理所作的修改，都應當理解為落入本發明的保護範圍。