針對多目標優化問題的導引式局部搜索遺傳算法的製作方法
2023-06-04 06:27:51 2
本發明涉及作業車間領域,具體地涉及用算法求解多目標柔性作業車間調度問題。
背景技術:
柔性作業車間調度問題是經典作業車間調度問題的延伸,每一道工序允許在一組給定的設備上加工。因此柔性作業車間調度問題,除了確定每一臺設備上的工序加工順序以外,還需要為每一道工序分配一臺合適的設備。柔性作業車間調度問題屬於NP—Hard問題。在現實生產中,往往還需要面對優化多個目標,並且每個目標之間相互影響和衝突。因此,一般地多目標問題不存在一個唯一的最優解對所有的目標都是最好的。目前,已經有很多技術用來解決柔性作業車間調度問題和多目標優化問題,其中進化算法、局部搜索、綜合性算法等方式都取得了很好的結果,但時間和空間複雜度的問題還需進一步解決。隨機加權法在多目標問題中也廣泛應用,但是權值並不能完全代表問題的重要性,不能準確滿足現實需求。針對這些不足,本發明提出一種導引式的局部搜索算法,結合遺傳算法和非支配排序策略解多目標優化問題。
技術實現要素:
針對上述不足,本發明要解決的問題是提供一種導引式局部搜索算法,結合遺傳算法和非支配排序策略解多目標優化問題。
本算法的目標是:第一.解決遺傳算法在遺傳操作過程中近親不斷交叉繁衍導致收斂過快,種群多樣性不足;第二.柔性作業車間問題的一個給定方案,它的鄰域通常通過從一臺設備上移動工序到另一臺設備上獲得,但是並不是所有的移動都會改進當前解;第三.枚舉完所有的鄰域解計算成本很高;第四.隨機加權的方式不能很好地解決多目標問題。
本發明針對其技術問題採用的技術方案是:第一.交叉變異之前計算近親指數和變異率,局部搜索得到的解只對子代中部分最差的解做替換;第二.通過移動關鍵路徑上關鍵工序,並根據移動對優化目標影響限制移動方向;第三.只對一部分的解進行鄰域搜索;第四.快速非支配排序法選擇Pareto最優解,相同等級的解通過擁擠距離選擇。
該技術方案的實施步驟如下:
步驟1:採用隨機的方法分別產生染色體的工序順序和設備選擇兩個部分作為初始解,初始種群規模為N;
步驟2:判斷是否達到最大迭代次數,達到則返回Pareto最優解,結束;未達到則執行下一步驟;
步驟3:將當前的解與精英記憶中的解組合,應用快速非支配排序和擁擠距離評估組合中的個體,前N個最優解會用來更新當前解;
步驟4:對評估後的個體用非支配排序得到不同等級的個體,優先選擇等級較低即支配的個體參與進化,用擁擠距離的策略來選擇參與進化的個體;
步驟5:基因進行交叉之前,對將進行交叉的兩個染色體的血緣關係進行計算,並根據血緣關係計算新產生染色體的變異率,從而避免算法早熟;
步驟6:以交叉概率pc對選擇的染色體進行交叉操作;
步驟7:以變異概率v進行變異操作
步驟8:導引式局部搜索:
步驟8.1:解碼子代種群,應用快速非支配法將子代種群排序,選擇子代種群中x%的最優解執行導引式局部搜索;
步驟8.2:解碼導引式局部搜索的解,應用快速非支配法將他們排序,用嚮導性搜索的最好的解替換子代種群中y%的最差的解;
步驟9:選擇子代種群中等級排名為1的解更新精英記憶;
步驟10:返回步驟2判斷最大迭代次數,循環;
本發明的有益效果是:第一.動態的變異率通過在收斂的後期增加變異概率保證了種群的多樣性,且導引式局部搜索的最優解只對子代的部分最差個體進行替換,也避免了算法早熟;第二.通過限定局部搜索的方向和範圍,避免了很多不必要的移動,大大減小了計算成本;第三.只對子代種群中的部分解做局部搜索,控制了計算時間和空間;第四.快速非支配排序和擁擠距離選擇方式對多目標優化問題更有效,獲得的Pareto最優解使多個目標都能同時更優。
附圖說明
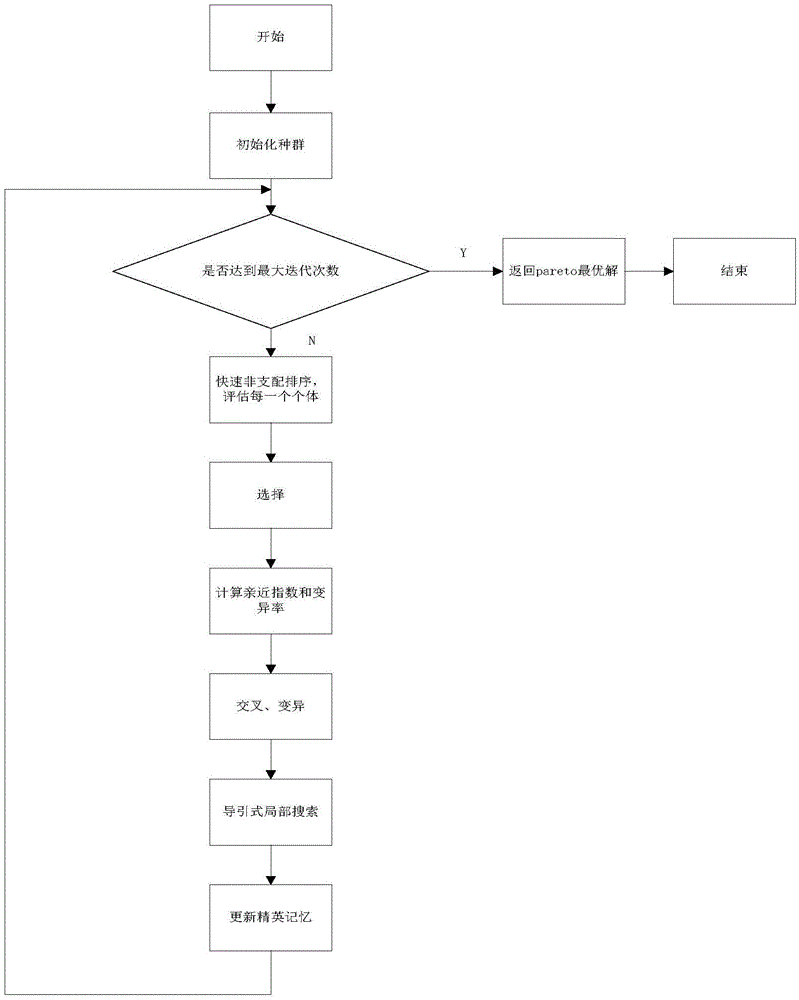
圖1表示本算法的流程圖
圖2表示一個3個工件3臺設備的柔性作業車間問題實例。
圖3表示本發明算法的編碼方式示例。
圖4表示兩個染色體交叉的過程圖示說明。
圖5表示一個染色體編譯過程圖示說明。
圖6表示選擇x%的個體進行導引式局部搜索的圖示說明。
圖7局部搜索中關鍵工序插入位置圖示說明。
具體實施方式
為了使本發明的目的、技術方案及優點更加清楚明白,以下結合附圖和實施例對本發明進一步詳細說明。應當理解此處所描述的具體實施例僅僅用於解釋本發明並不用於限定本發明。基於本發明中的實施例,本領域技術人員在沒有作出創造性勞動前提下所獲得的所有其他實施例,都屬於本發明保護的範圍。
本發明針對現有遺傳算法遺傳操作過程中近親不斷交叉繁衍導致收斂過快,種群多樣性不足的問題設計了在交叉前進行交叉指數和變異率的計算,針對領域解的成本過高,本算法只對部分解進行局部搜索且控制搜索範圍和方向,減少了成本。
下面結合附圖詳細說明。
多目標柔性作業車間調度問題結合圖2(圖中「-」表示該設備不能加工改到工序)可以表述如下:n個獨立工件的集合J={J1,J2,…,Jn},m臺設備的集合M={M1,M2,…,Mm},工件Ji由ni個優先約束的工序序列組成,這些工序根據給定的序列一個接一個的加工。每一道工序Oi,j表示工件Ji的第j道工序,必須從給定的一個子集Mi,j∈M中選擇一臺設備加工。工序的加工時間由設備決定。pi,j,k表示Oi,j在設備Mk上的加工時間。調度安排包括兩個子問題:分配每一道工序一個合適的設備的路徑子問題和確定所有設備上的工序序列的排序子問題。
令Ci表示工件Ji的完工時間,Wk表示設備Mk的工作量,它是所有在設備Mk上加工的工序的加工時間之和,優化目標是:
⑴最小化總完工時間:F1=max{Ci|i=1,…,n}
⑵最小化關鍵設備工作量:F2=max{Wk|k=1,…,m}
⑶最小化所有設備總工作量:F3=Σpi,j,k
任務是在所有目標都被考慮的情況下找到一組解優於其他解。
為了簡化問題,做了如下假設:所有設備在t=0時刻都是可用的,每一個工件都有獨立的釋放時間,每一臺設備在同一時刻只能加工一道工序,一道工序一旦開始加工不允許中斷,每一個工件的工序順序是預定的不能修改,忽略設備的設置時間和工序之間的轉換時間。
針對給定的條件以及要解決的問題,結合圖1本算法的詳細步驟如下:
步驟1:採用隨機的方法分別產生染色體的工序順序和設備選擇兩個部分作為初始解,初始種群規模為N;
柔性作業車間調度問題的編碼既要給出加工工序的先後順序,同時還需為每個工序選擇加工機器,因此,本文採用基於工序和設備的雙重編碼方法:工序編碼部分按照工件號編碼,工件包含幾道工序在該工件號出現幾次;設備編碼部分按照設備編碼編碼,每一個工件的每一道工序對應一臺設備編號。圖3給出了圖2所示問題的一條可行染色體。
如圖3所示,基於工序和設備的雙層整數編碼由兩部分組成:第一部分為確定工序加工順序的編碼;第二部分為每道工序選擇加工設備的編碼。因此,圖3中的染色體表示:3個工件,7道工序,在3臺設備上加工,該染色體解碼表示的加工順序為:O3,1,1,O1,1,3,O3,2,3,O2,1,2,O2,2,3,O1,2,2,O2,3,1.Oi,j,k表示工件i的第j道工序在設備k上加工。如O3,1,1表示工件3的第一道工序在設備1上加工。
步驟2:判斷是否達到最大迭代次數,達到則返回Pareto最優解,結束;未達到則執行下一步驟;
步驟3:將當前的解與精英記憶中的解組合,應用快速非支配排序和擁擠距離評估組合中的個體,前N個最優解會用來更新當前解;
所述快速非支配排序:將當前種群中的所有非支配解分配給最高等級1,然後將最高級別1中的解暫時從種群中除去,剩下種群中所有的非支配解分配給第二級別2,以此類推,給所有的個體賦予非支配等級。
個體之間的擁擠距離計算如下:
式中,P[i]dis表示個體i的擁擠距離,P[i]k表示個體i在子目標k的函數值。
步驟4:對評估後的個體用非支配排序後不同等級的個體,優先選擇等級較低即支配的個體參與進化,用擁擠距離的策略來選擇參與進化的個體;
相對於單目標優化問題,多目標優化問題的選擇操作更加複雜,一般包括個體的等級排序和相同等級非支配解的選擇策略。本發明採用快速非支配排序法對種群中的個體排序,採用擁擠距離來選擇相同級別的個體。
對於非支配排序後等級不同的個體,優先選擇等級較低即支配的個體參與進化。也就是從第二步的解中隨機選擇兩個解A和B。如果A支配B,複製A到子代種群,反之亦然。當需要從同一等級選擇個體時,採用擁擠距離的策略來選擇參與進化的個體。即如果A和B是非支配的,他們更大的擁擠距離值將用來選擇最好的一個插入到子代。
步驟5:基因進行交叉之前,對將進行交叉的兩個染色體的血緣關係進行計算,並根據血緣關係計算新產生染色體的變異率,從而避免算法早熟;
計算程序如下:
設P1,p2為待交叉的兩個染色體,n為染色體中基因的總數,s為近親指數,v為子代的變異率:
步驟6:以交叉概率pc對選擇的染色體進行交叉操作;
結合圖4交叉操作過程可以描述如下:對工序順序部分:隨機選擇父代1中的任意兩點,兩點之間的基因直接複製到子代1,剩餘部分由父代2中對應的工序按照原來的順序填滿,子代2按照對稱的方式產生。對設備選擇部分:隨機選擇父代1和父代2中的若干列,將父代1和父代2中列對應的基因設備相互交叉,其餘部分保留到各自的子代。
步驟7:以變異概率v進行變異操作
結合圖5一條染色體的變異過程,變異操作可以描述如下:對工序順序部分:隨機選擇一個工序,將其插入到序列中的另外一個位置。對設備選擇部分:隨機選擇一個設備,在其對應的工序的可選擇的加工設備集合中選擇另一臺設備替換該基因片段。
步驟8:導引式局部搜索:
步驟8.1:解碼子代種群,應用快速非支配法將子代種群排序,選擇子代種群中x%的最優解執行導引式局部搜索;
步驟8.2:解碼導引式局部搜索的解,應用快速非支配法將他們排序,用嚮導性搜索的最好的解替換子代種群中y%的最差的解;
步驟9:選擇子代種群中等級排名為1的解更新精英記憶;
選擇子代種群中等級排名為1的解更新精英記憶。如果一個解C支配精英記憶中的任何其他解,刪除這些解,將C複製到精英記憶。如果C對精英記憶中其他結果都是非支配的,C也複製到精英記憶。
步驟10:返回步驟2判斷最大迭代次數,循環操作;
所述步驟8.1、8.2可結合圖6局部搜索方式描述如下:為了減小算法的計算時間,步驟8.1中,只有子代種群中最優解的x%選擇來進行局部搜索。為了保證下一代的多樣性,我們不完全將子代種群中的解用導引式局部搜索的結果替換。只有最大y%的最差解被步驟8.1的最優解替換。x和y是兩個預定義的參數。
所述導引式局部搜索尋找可移動工序及可行位置的程序如下:
⑴找到關鍵路徑上所有的中工序插入到集合U
⑵對於集合U中的每一個工序Oi,j,在設備Mk上的加工時間為pi,j,k,確定所有可以加工工序Oi,j的其他設備。如果滿足以下條件之一插入Oi,j,可替代的設備Mk′記入集合V。
a)工序Oi,j,在設備Mk′上的加工時間pi,j,k′小於pi,j,k(改進總延遲)
b)設備Mk的工作量等於關鍵設備工作量值MW,設備Mk′插入工序Oi,j之後新的工作量小於關鍵設備工作量MW(改進關鍵工作量)
c)只有一條關鍵路徑。新的加工時間是pi,j,k,最早開工時間pest(Oi,j)小於Oi,j在設備Mk上的加工時間(關鍵設備工作量和總工作量沒有改變,總完工時間改進)
⑶每一道工序Oi,j和它對應的集合V中的設備Mk′,發現設備Mk′上的合適的位置:刪除工序Oi,j和它對應的集合V中的設備Mk′
⑷如果設備Mk′上沒有工序,插入工序Oi,j到設備Mk′。否則找到設備Mk′上一道工序Op,q的位置,pest(Oi,j)小於工序Op,q的當前開始時間。
⑸如果pest(Oi,j)加上工序Oi,j在設備Mk′上的加工時間pi,j,k′最多為設備Mk′上工序Op,q的下一道工序Or,s的開始時間,插入Oi,j到Op,q之後
⑹如果Or,s沒有在關鍵路徑上,插入Oi,j到Op,q之後。否則,如果Oi,j+1沒有在關鍵路徑上,插入Oi,j到關鍵塊B之後。如果Oi,j+1和關鍵塊B都在關鍵路徑上,應用定理1找到最好的移動
⑺如果集合U中沒有工序,停止,否則返回第(3)步。
所述導引式局部搜索可以給出如下說明:由於柔性作業車間調度問題的一個給定的調度方案,它的鄰域可以通過從一臺設備移動一個工序到另外一臺設備上獲得,但是,不是所有的移動都會改進當前解,並且枚舉完所有的鄰域將是非常昂貴的。導引式局部搜索解決了怎樣找到最好的移動來同時改進多個目標的問題。
所述導引式局部搜索的具體程序提到的相關名詞可結合圖7局部搜索中關鍵工序插入位置作出如下描述:一個調度方案的關鍵路徑即是一個工序序列,其總的加工時間是所有工件都要完成的最短時間,一個調度方案有不止一條關鍵路徑;關鍵塊是關鍵路徑上同一加工設備上連續的工序集合,一個給定的關鍵路徑一個設備可能不止與一個關鍵塊有關;關鍵設備可以表述為如下:如果設備Mk的工作量等於關鍵設備工作量,我們稱設備Mk為最大負載設備,表示為一個函數:WL(Mk)=MW,一個調度方案不止擁有一臺最大負荷設備。pest(Oi,j):一道工序優先權最早開始時間pest(Oi,j)等於他的工件緊前工序Oi,j-1的完工時間。如果Oi,j是工件的第一道工序,pest(Oi,j)等於對應工件的釋放時間。令st(Oi,j)表示Oi,j在設備Mk′上的開工時間。等於pest(Oi,j)和Op,q完工時間的最大值。令stop(B)是關鍵塊B的完工時間。我們引入兩個值:位置值1,位置值2來評估之前描述的兩個位置使Cmax增加的數量。
位置值1=max(st(Or,s)-(st(Oi,j)+pi,j,k′),st(Oi,j+1)-(st(Oi,j)+pi,j,k′))
位置值2=stop(B)+pi,i,k′-st(Oi,j+1)
定理1:如果位置值1≤位置值2,將Oi,j插入到Or,s之前比將Oi,j插入到關鍵塊B之後增加總完工時間Cmax要小。否則,插入到關鍵塊B之後增加的總完工時間Cmax更小。
