一種液態雲微物理參數的反演方法與流程

2023-10-18 10:03:24

本發明涉及一種利用毫米波雲雷達獲取的反射率因子反演液態雲微物理參數的方法，特別涉及一種結合最優估計理論和經驗公式的液態雲微物理參數的反演方法。

背景技術：

雲的全球分布及其微物理結構影響全球氣候與環境變化，且對地球-大氣系統的輻射收支平衡和水汽循環有著重要調節作用，通過觀測全球雲層特徵，得到從薄雲到濃厚雲的垂直剖面特徵，反演得到測量雲水含量、雲粒子尺寸以及其他參量，對氣候研究、精細化天氣過程分析、天氣預測、人工影響天氣等方面具有重要意義。

隨著測雲技術的快速發展，國內外學者不斷深入研究雲微物理參數的反演方法，取得了一些應用成果。傳統的雲物理參數反演主要藉助統計分析得到的經驗關係算法來完成，即以大量的實驗數據為基礎，利用函數擬合的方式建立雷達反射率與雲物理參數的關係。

例如Atlas、Sauvageot、Kropfli和Kelly、Fox和Illingworth等人結合35GHz雷達和飛機穿雲實測譜參數數據，得到雷達反射率與粒子有效半徑、液水含量之間的函數關係，為指數形式；

Neil等人利用8mm地基雲雷達探究了層雲的雲水含量和有效粒子半徑大小，驗證雷達反射率因子、粒子有效半徑、雲內液態水含量三者之間關係，結果與Atlas和Sauvageot的結果吻合。

Austin和Stephens基於最優估計理論，開發了一種基於最優估計的液態雲微物理參數的業務化反演算法，利用先驗數據信息，在狀態向量(待反演參量)和先驗數據差分以及已知測量向量(雷達反射率因子)和前向模型值差分的加權之和最小時，得到液態雲微物理參數。

現有技術中常用的經驗反演的優點在於計算簡單，需要大量的探測數據進行統計分析，且根據觀測地點、時間和雲類的區別關鍵反演係數有所不同，但算法適用性和擴展性較差，例如，當雲內存在毛毛雨降水時，由於降水粒 子對雲內液水含量的貢獻很小，利用Atlas經驗公式反演得到的結果偏大，需要統計出適用於毛毛雨和小雨的關係式。最優估計反演精度受到先驗數據的影響，目前採用觀測統計值為先驗數據，存在一定的局限性和不足。

專利方面，安徽師範大學提出「一種利用A-Train系列衛星數據協同反演雲相態和雲參量的新方法」(公開號：CN102707336A)與中國氣象局氣象探測中心提出了「一種雲雷達與衛星探測數據融合方法及系統」(公開號：CN105445816A)，系統採用神經網絡訓練，建立亮溫與雲頂高度、雲底高度和反射率因子的關係；北京無線電測量研究室提出了「一種毫米波雲雷達的數據融合方法及系統」(公開號：CN104345312A)，系統融合雷達多模式工作方式得到的探測數據，提高數據質量和探測效率。此外，在探測手段方面，南京信息工程大學申請了「一種雲粒子探測方法及探測器」(公開號：CN105115862A)的專利，利用雲粒子的散射信號探測得到雲粒子相態和雲粒子大小；中國空間技術研究院申請了「一種用於測雲的地面太赫茲雷達系統」(公開號：CN104569980A)以及「一種基於太赫茲主動測雲雷達的測雲實驗裝置及方法」(公開號：CN104597454A)。在所檢索到的相關專利中，國內外的相關研究主要集中在雲探測設備或儀器，部門單位提出了多源數據融合處理方法，雲反演方法的研究較少。

技術實現要素：

本發明的目的根據毫米波雲雷達提供的雷達反射率因子，基於最優估計理論，採用經驗公式計算值為先驗值，假設粒子譜服從對數正態分布，建立雷達反射率因子與液態雲物理參數的函數關係，在待反演參量和先驗數據以及雷達反射率因子和函數計算值的差值加權取得最小值的情況下求得反演最優解。

為了實現以上目的，本發明是通過以下技術方案實現的：

一種液態雲微物理參數的反演方法，反演算法在代價函數取得最小值的情況下求得最優解，所述代價函數為狀態向量和先驗數據差分以及已知測量向量和前向模型值差分的加權之和，

式中，xa為根據雷達反射率因子計算得到的先驗數據，Sa為先驗數據的協方差矩陣，F(x)為雷達反射率因子的前向物理模式，Sy是雷達反射率因子 測量誤差的協方差矩陣，y為測量向量即雷達反射率因子，x為未知的狀態向量即待反演參量，所述待反演參量包括雲粒子數密度、幾何平均半徑和分布寬度參數。

將先驗數據xa作為迭代初值，通過連續最小化代價函數D，最終求得待反演參量x的迭代解。

優選地，假設大氣中的雲粒子的尺度分布符合對數正態分布，依此建立雷達反射率因子與液態雲物理參數即雲粒子數密度，雲粒子有效半徑，雲粒子分布寬度參數的函數關係；

式中：NT是雲粒子數密度；r是雲粒子有效半徑；rg是幾何平均半徑；σlog是分布寬度參數，為無量綱變量；σg為幾何標準差；ln代表自然對數變換；橫線表示求算術平均值。

在未降雨或有小雨，或有毛毛雨的情況下，認為雲粒子尺度足夠小，滿足瑞利散射條件，根據云內液態水含量CLW、雲粒子有效半徑re和雷達反射率因子Z的定義，推導得到下列公式。

式中：ρω代表水密度。

優選地，所述先驗數據xa與先驗數據的協方差矩陣Sa根據由歷史統計數據得到粒子數密度NT和分布寬度σlog來計算得到，

式中，距離庫zi；z1和zn分別代表雷達廓線中雲底和雲頂的距離庫，下標a表示狀態向量x的先驗值，rga、NTa和σloga是分別代表雲粒子有效半徑、粒子數濃度和分布寬度的先驗值。

優選地，通過雲粒子尺寸即雲粒子有效半徑re、粒子數濃度NT和分布寬度σlog，推算出所述雷達反射率因子的前向物理模式F(x)；

通過前向物理模式F(x)建立測量向量y與狀態向量x兩者之間的關係，前向物理模式可表示為

y＝F(x)+εy

式中εy表示測量誤差，ZFM(zi)為各距離庫zi的雷達反射率因子；z1和zn分別代表雷達廓線中雲底和雲頂的距離庫。

優選地，通過雷達反射率因子的定義公式推導計算各距離庫zi的雷達反射率因子ZFM(zi)；

K＝(m2-1)/(m2+2)

式中，m表示復折射指數。優選地，所述測量向量y與未知的狀態向量x為

式中：ZdB(zi)、rg(zi)、NT(zi)和σlog(zi)分別代表雷達反射率因子、幾何平均半徑、雲粒子數密度和分布寬度參數在距離庫zi處的值；n代表廓線內的雲距離庫數。

優選地，對於每條觀測廓線，狀態向量x為每個距離庫內的待反演參量，已知測量向量y僅有對應距離庫內的雷達反射率因子，需要藉助先驗數據xa對反演進行約束，保證迭代收斂以及反演結果的可靠性。

優選地，所述將先驗數據xa作為迭代初值，通過連續最小化代價函數D，求得待反演參量x的迭代解，且在進行迭代計算時滿足迭代的收斂條件；

式中：上標i和i+1表示迭代次數，L代表前向物理模式對狀態向量x的靈敏度。

優選地，所述迭代的收斂條件為：

式中：Sx是迭代狀態向量的誤差協方差矩陣，表示三個待反演物理量的方差以及各參量之間的協方差，Sy是雷達反射率因子測量誤差的協方差矩陣。

與現有技術相比，本發明有益效果是：

本發明可彌補傳統的經驗公式適用性差的缺點，而且除了常見的雲粒子半徑和雲水含量，還可得到粒子數濃度和分布寬度，反演的到的結果更為全 面；由於採用了實時觀測的雷達反射率因子來計算先驗值，提高了反演結果精確性。

附圖說明

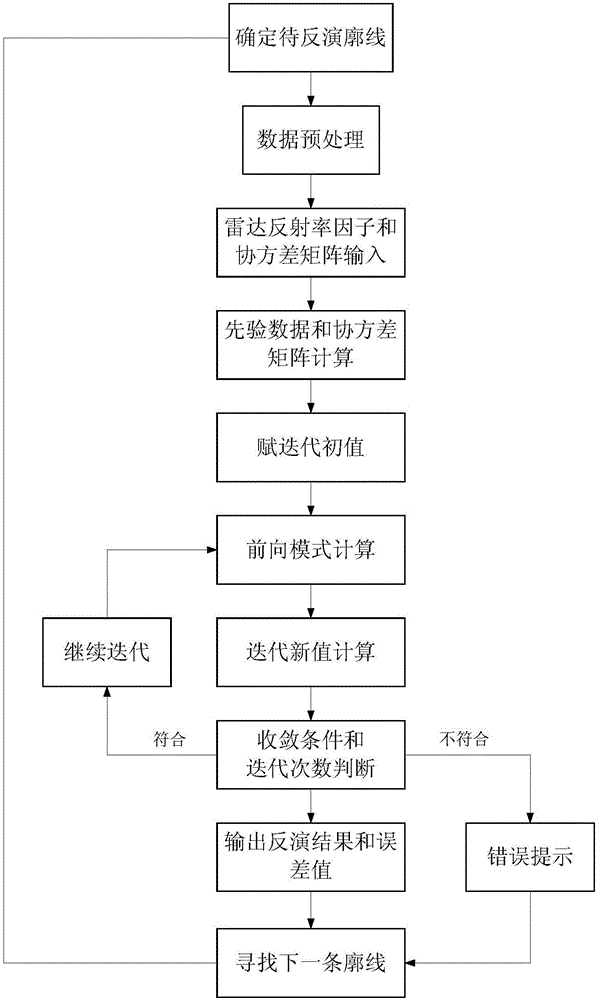
圖1是本發明一種液態雲微物理參數的反演方法的流程圖；

圖2是本發明一種液態雲微物理參數的反演方法的一個實施例中採用的雲粒子半徑先驗數據示意圖；

圖3是本發明一種液態雲微物理參數的反演方法的一個實施例中反演得到的液態雲微物理參數示意圖。

具體實施方式

以下結合附圖，通過詳細說明一個較佳的具體實施例，對本發明做進一步闡述。

毫米波雲雷達利用雲粒子對電磁波的散射特性，通過對雲的雷達回波分析了解雲的宏觀和微觀特性，即可探測直徑從幾微米到弱降水粒子，連續檢測雲的垂直剖面。回波強度反映了雲中粒子的大小和濃度，回波強度在時間和空間上的變化反映了雲微物理過程演變特徵。對雷達所測的反射率因子進行預處理，即可得到有雲區域內的連續、有效的廓線和剖面回波數據，及其誤差信息。

如圖1所示，一種液態雲微物理參數的反演方法，

反演算法在代價函數取得最小值的情況下求得最優解，所述代價函數為狀態向量和先驗數據差分以及已知測量向量和前向模型值差分的加權之和，

式中，xa為根據雷達反射率因子計算得到的先驗數據，Sa為先驗數據的協方差矩陣，F(x)為雷達反射率因子的前向物理模式，Sy是雷達測量誤差的協方差矩陣，y為測量向量即雷達反射率因子，x為未知的狀態向量即待反演參量，所述待反演參量包括雲粒子數密度、幾何平均半徑和分布寬度參數。

將先驗數據xa作為迭代初值，通過連續最小化代價函數D，最終求得待反演參量x的迭代解。

假設大氣中的雲粒子的尺度分布符合對數正態分布，依此建立雷達反射率因子與液態雲物理參數即雲粒子數密度，雲粒子有效半徑，雲粒子分布寬 度參數的函數關係；

式中：NT是雲粒子數密度；r是雲粒子有效半徑；rg是幾何平均半徑；σlog是分布寬度參數，為無量綱變量；σg為幾何標準差；ln代表自然對數變換；橫線表示求算術平均值。

對於先驗數據獲取及計算，根據經驗公式，由雷達有效反射率因子計算得到雲粒子半徑和液水含量。前人利用雲雷達以及其它雲粒子譜探測設備，測出雲粒子的滴譜分布、粒子數濃度、粒子有效半徑和雲內液態水含量，進行大量數據的統計擬合得出雲雷達反演粒子半徑和液態水的經驗關係，得出經典的常用經驗公式，

Z＝138×10-12D6 (4)

其中CLW代表雲內液態水含量，D為粒子直徑，Z是毫米波雲雷達測得的雷達反射率因子。

在未降雨或有小雨，或有毛毛雨的情況下，認為雲粒子尺度足夠小，滿足瑞利散射條件，根據云內液態水含量CLW、雲粒子有效半徑re和雷達反射率因子Z的定義，推導得到下列公式。

式中：ρω代表水密度。

所述先驗數據xa與先驗數據的協方差矩陣Sa根據由歷史統計數據得到粒子數密度NT和分布寬度σlog來計算得粒子數濃度和分布寬度由歷史統計數據得到，並依此計算先驗數據的協方差矩陣。

式中，距離庫zi；z1和zn分別代表雷達廓線中雲底和雲頂的距離庫，下標a表示先驗值，rga代表雲粒子有效半徑的先驗數據，同理，NTa和σloga是分別代表粒子數濃度和分布寬度的先驗值。

所述的雷達反射率因子的前向物理模式F(x)是通過已知的雲粒子尺寸即雲粒子有效半徑re、粒子數濃度NT和分布寬度σlog，推算出雷達反射率因子的前向物理模式F(x)；即考慮毫米雲雷達接收給定距離的雲粒子散射能量時，所經路徑上的雙向衰減，得到經衰減訂正後的雷達反射率因子ZFM；通過雷達反射率因子Z的定義公式推導計算各距離庫zi的雷達反射率因子ZFM(zi)；

K＝(m2-1)/(m2+2) (12)

式中，z1和zn分別代表雷達廓線中雲底和雲頂的距離庫，下標FM表示前向物理模式計算值，m表示復折射指數。

通過前向物理模式F(x)建立測量向量y與待反演參量x兩者之間的關係，前向物理模式可表示為

y＝F(x)+εy (13)

式中εy表示測量誤差。

所述測量向量y與未知的狀態向量x為

式中：ZdB(zi)、rg(zi)、NT(zi)和σlog(zi)分別代表雷達反射率因子、幾何平均半徑、雲粒子數密度和分布寬度參數在距離庫zi處的值；n代表廓線內的雲距離庫數。

對於每條觀測廓線，狀態向量x為每個距離庫內的待反演參量，已知測量向量y僅有對應距離庫內的雷達反射率因子，需要藉助先驗數據xa對反演進行約束，保證迭代收斂以及反演結果的可靠性。

所述將先驗數據xa作為迭代初值，通過連續最小化代價函數D，求得待反演參量x的迭代解，且在進行迭代計算時滿足迭代的收斂條件；

式中：上標i和i+1表示迭代次數，L代表前向物理模式對狀態向量x的靈敏度。

所述迭代的收斂條件為：

式中：Sx是迭代狀態向量的誤差協方差矩陣，表示三個待反演物理量的方差以及各參量之間的協方差，Sy是雲雷達測量誤差的協方差矩陣。

反演誤差主要來源於雷達反射率因子和先驗數據獲取算法，根據誤差傳遞理論，計算出反演的待反演參數的標準差和誤差，也稱為不確定度。

根據所述液態雲微物理參數的反演方法，採用CloudSat實測數據實現反演過程，並分析反演結果。所選反演個例為層積雲，反演採用的雲粒子半徑先驗數據如圖2所示，與現有反演過程中採用的固定先驗數據相比(即有效半徑先驗數據為固定值，且不隨高度和經緯度變化)，由實測雷達反射率因子計算得到的有效粒子半徑更能反映雲物理參數的真實特性。

反演得到的液態雲微物理參數結果如圖3所示。雲微物理參數包括有效粒子半徑、液態水含量、粒子數濃度和分布寬度參數，有效粒子半徑和雲中液態水含量的最大值出現在雲層中部雷達回波較強的區域，雲粒子數濃度呈現隨高度增加逐漸增大的趨勢，分布寬度參數則隨高度增加逐漸減小，各參數的空間分布和變化趨勢與CloudSat發布結果基本一致，且符合國內外學者統計的晴天積雲的雲滴特徵參數範圍，反演結果可信。

儘管本發明的內容已經通過上述優選實施例作了詳細介紹，但應當認識到上述的描述不應被認為是對本發明的限制。在本領域技術人員閱讀了上述內容後，對於本發明的多種修改和替代都將是顯而易見的。因此，本發明的保護範圍應由所附的權利要求來限定。