基於最小二乘法的單相電壓跌落檢測方法與流程
2024-03-08 04:29:15 2
本發明屬於電力系統狀態監測領域,尤其涉及一種基於最小二乘法的單相電壓跌落檢測方法。
背景技術:
動態電壓恢復器(Dynamic Voltage Restorer,DVR)是一種用於保證敏感負荷供電電壓穩定的有效串聯補償裝置,可在毫秒級時間內向系統與負荷之間串聯注入幅值和相位可調的電壓,補償電壓暫降,從而保證敏感負荷的電壓在受到系統電壓擾動時仍處於可接受的範圍內。
DVR為了滿足檢測的實時性要求,常見的三相暫降檢測方法有dq變換、αβ變換等,上述算法雖然簡單,但是檢測的速度受諧波影響大。而單相檢測方法有基於傅立葉變換的檢測法、考慮相位跳變的檢測法等,這些方法也都無法很好地解決由諧波造成的帶寬增加、檢測時間延長等問題。
技術實現要素:
本發明的目的在於提供一種解決諧波存在時的快速檢測電網電壓跌落的檢測方法,涉及到系統中的諧波含量檢測和跌落快速檢測。
實現本發明目的的技術方案為:一種基於最小二乘法的單相電壓跌落檢測方法,包括以下步驟:
步驟1,將含有各次諧波的周期電壓信號表示成三角函數形式的傅立葉級數,建立電壓模型;
步驟2,將步驟1中得到的電壓模型離散化,並用矩陣形式進行表示;
步驟3,根據最小二乘原理,通過不斷縮小實際電壓採樣值與步驟2建立的電壓模型相減得到的誤差的平方和,修正電壓模型中各分量參數,得到符合實際情況的電壓模型;
步驟4,再次利用最小二乘法原理對電壓信號的實時採樣值與建立模型的差值進行檢測,利用協方差矩陣得到相應的基波及各次諧波的參數信息,將得到的電壓基波幅值與設置的電壓跌落補償閥值進行比較,當基波幅值低於電壓跌落補償閥值時視為發生跌落。
與現有技術相比,本發明的顯著優點為:
(1)本發明減小了諧波模型與實際電網電壓波形的差異,通過基於FFT的諧波分析,將模型參數進行修正,得到最優的模型參數;
(2)本發明利用優化後的模型參數,進行跌落電壓檢測,穩態誤差較小,敏感度高,可以快速檢測到電壓跌落。
附圖說明
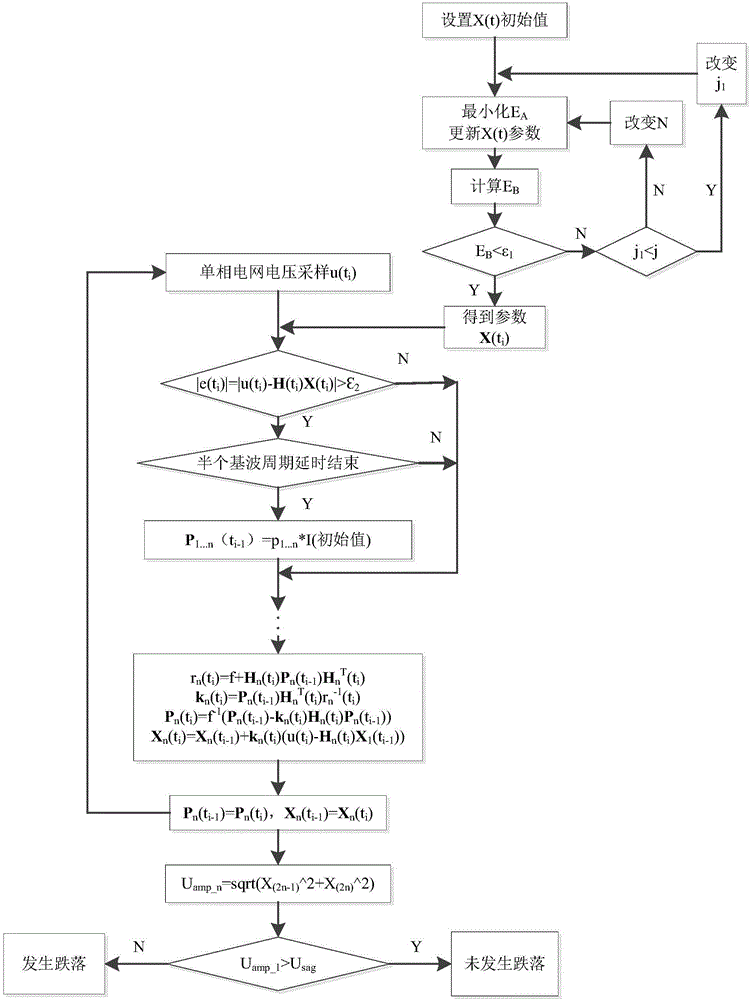
圖1為本發明的基於最小二乘法的單相電壓跌落檢測方法流程圖。
圖2(a)為電壓跌落20%時基波檢測波形圖。
圖2(b)為電壓跌落20%時三次諧波檢測波形圖。
圖2(c)為電壓跌落20%時五次諧波檢測波形圖。
圖2(d)為電壓跌落20%時七次諧波檢測波形圖。
圖3(a)為電壓跌落60%時基波檢測波形圖。
圖3(b)為電壓跌落60%時三次諧波檢測波形圖。
圖3(c)為電壓跌落60%時五次諧波檢測波形圖。
圖3(d)為電壓跌落60%時七次諧波檢測波形圖。
具體實施方式
結合圖1,本發明的一種基於最小二乘算法的電壓跌落檢測方法,包括以下步驟:
步驟1,將含有各次諧波的周期電壓信號表示成三角函數形式的傅立葉級數,建立電壓模型:
其中,u(t)為周期電壓信號,周期為T1,基波角頻率Un,ωn,分別為單相電網電壓中對應的基波和各次諧波分量的幅值、角頻率及起始相角,n=1,2,...N,N為最高諧波次數;
步驟2,將步驟1中得到的電壓模型離散化,並用矩陣形式進行表示:
u(ti)=H(ti)x(ti)
H(ti)=[cosω1ti-sinω1ti…cosωNti-sinωNti] (2)
其中,u(ti)表示離散後的電壓信號,H(ti)和x(ti)為(1)式中等式右邊的展開矩陣表達形式;
步驟3,根據最小二乘原理,通過不斷縮小實際電壓採樣值與步驟2建立的電壓模型相減得到的誤差的平方和,修正電壓模型中各分量參數,得到符合實際情況的電壓模型;具體為:
步驟3-1、將採樣數據分成兩組A(n)和B(n),長度分別為j1和j-j1,其中j是採樣數據總長度,且j1>j-j1;
步驟3-2、計算A(n)的誤差的平方和:
其中,f是遺忘因子,f∈(0,1),X(ti)為x(ti)的估計值,對EA進行最小化,得到相應的估計值X(ti);
步驟3-3、將步驟3-2得到的X(ti)帶入組B(n)進行驗證,相應的誤差平方和為:
定義誤差閾值ε1,若EB≥ε1則估計值誤差大,重新調整諧波次數N和j1,然後重複步驟3-2和步驟3-3,若EB<ε1,則估計值作為系統電壓模型的參數;
步驟4,再次利用最小二乘法原理對電壓信號的實時採樣值與建立模型的差值進行檢測,利用協方差矩陣得到相應的基波及各次諧波的參數信息,將得到的電壓基波幅值與設置的電壓跌落補償閥值進行比較,當基波幅值低於電壓跌落補償閥值時視為發生跌落;具體為:
根據步驟3得到的估計值X(ti),最小二乘法算法表達式為:
其中,Hn(ti)=[cosωnti -sinωnti],Xn(ti)是狀態向量xn(ti)的估計值;Pn(ti-1)是第i-1次迭代的二維協方差矩陣,初始值為p1...nI,p1...n=(p1,p1,p2,p2,…,pn,pn)為初始變量,I為單位矩陣;rn(ti)與kn(ti)為最小二乘法算式的中間變量;
單相電網電壓的基波幅值為:
假設電壓跌落補償閥值為Usag,若Uamp_1>Usag則表明未發生跌落,若Uamp_1≤Usag則表明發生跌落;
最小二乘法的誤差e(ti)為:
e(ti)=u(ti)-H(ti)X(ti) (7)
設置閾值ε2,當誤差e(ti)大於閾值ε2時,判定當前電網電壓出現暫降過程,將進入待補償狀態,同時將協方差矩陣Pn(ti-1)重置為初始值;當誤差e(ti)小於等於閾值ε2時,則判定電網電壓在正常範圍內,不進行補償,無需對協方差矩陣進行重置;
設置半個基波周期延時,當檢測到誤差e(ti)大於閾值ε2時重置協方差,同時進入延時程序,屏蔽協方差重置直到延時結束才能再次重置協方差。
下面結合具體實施例對本發明作進一步說明。
實施例
工業電網中的諧波通常是各種整流設備造成,這樣的諧波次數為奇數,而且隨著次數越高,諧波幅值越小。因此假如通過基於最小二乘法的諧波檢測,得到實際系統中的諧波分量,測得系統中的諧波為3、5、7次,有效值分別為20V,10V,5V。建立的含諧波電壓方程如下所示:
為了驗證在不同跌落情況下檢測的準度和快速性,分別設計了跌落20%及60%的實驗。
圖2為用測試儀模擬電網電壓20%的跌落,即跌落至原來的80%,實線為採樣波形,虛線為檢測波形,圖2(a)為基波量,圖2(b)為三次諧波量,圖2(c)為五次諧波量,圖2(d)為七次諧波量;圖中,標籤值代表了橫縱坐標值,橫坐標代表採樣點,縱坐標代表幅值。
圖3為用測試儀模擬電網電壓60%的跌落,即跌落至原來的40%,實線為採樣波形,虛線為檢測波形,圖3(a)為基波量,圖3(b)為三次諧波量,圖3(c)為五次諧波量,圖3(d)為七次諧波量;圖中,標籤值代表了橫縱坐標值,橫坐標代表採樣點,縱坐標代表幅值。
以上波形圖採用Matlab仿真得到,採樣點的採樣間隔為50us。從圖2和圖3中可以看出,檢測精度在0.1V,檢測速度為5-10ms,跌落深度對檢測的速度影響不大。
