一種核反應堆堆芯子通道計算的加速方法與流程

2023-12-11 01:26:07 1

本發明涉及核反應堆堆芯設計和安全領域，是一種核反應堆堆芯子通道計算的加速方法。

背景技術：

傳統的壓水堆全堆芯熱工水力分析一般採單通道模型，該模型認為堆芯各個通道之間是孤立的、封閉的，不考慮與相鄰通道之間的質量、動量和能量的交換，這種模型簡單，計算量小，但僅適用於計算閉式通道。因此發展了子通道模型，該模型認為相鄰通道冷卻劑之間存在質量、動量和能量的交換。由於考慮了這種交混效應，熱通道內冷卻劑的焓和溫度比不考慮交混時低，與之相應的燃料溫度也會有所下降，這有利於提高反應堆的安全性和經濟性。

但是，在子通道模型的計算中不能像單通道模型那樣只計算少數熱通道，而是對大量的通量進行分析，因此當進行全堆芯的子通道計算時，計算量和所消耗的計算機內存都是難以忍受的。因此，需要一種加速子通道計算和降低內存計算機消耗的方法。

技術實現要素：

為了克服上述現有技術存在的問題，本發明的目的在於提供一種核反應堆堆芯子通道計算的加速方法，是一種加速堆芯子通道計算同時降低內存消耗的方法，該方法通過採用Krylov子空間法求解全堆芯子通道計算中的大型非對稱線性方程組，包括能量方程、軸向動量 方程、壓力修正方程，具有較高的計算效率。

為了達到上述目的，本發明採用如下技術方案：

一種核反應堆堆芯子通道計算的加速方法，包括以下兩大步驟：

步驟1：將子通道質量、能量和動量守恆非線性方程組進行線性化，定義以下三個轉換函數fij、βkj和βij』以考慮施主元的影響：

式中，

mij——混合物軸向質量流量；

wkj為穿過間隔k的橫流速度，為正值，與eik一起表示方向，eikwkj大於0表示從l通道流到l′通道，否則相反；

——為間隔k的有效速度，即相鄰通道有效速度的代數平均；

將式(1)中的三個轉換函數代入到子通道能量、軸向動量、橫向動量和質量方程中，便得到如下四個線性化後的子通道方程：

1)能量方程

式中，

fij、fij-1——通道(i,j)和(i,j-1)的轉換函數；

mij、mij-1——通道(i,j)和(i,j-1)的混合物軸向質量流量；

ΔXj——軸向節塊j的高度；

w'kj——為穿過間隔k的湍流速度；

βkj——間隔k的轉換函數

wkj為穿過間隔k的橫流速度，為正值，與eik一起表示方向，eikwkj大於0表示從l通道流到l′通道，否則相反；

hij、hnj、hij+1和hij-1——通道(i,j)、(n,j)、(i,j+1)和(i,j-1)的混合物焓值；

Pr——燃料棒r的熱周，燃料棒r與通道i相鄰；

Φir——燃料棒r的熱周與通道i相鄰的份額；

q″rj——燃料棒到流體的熱流密度；

Ck——橫嚮導熱係數，如下式計算：

——以k為邊界相鄰的兩個通道i和n的導熱係數的代數平均值；

GT——導熱係數的幾何因子，用於考慮子通道間由於導熱引起的能量傳遞；

lk——相鄰兩個子通道的中心距

Tij、Tnj——通道(i,j)和(n,j)溫度；

2)軸向動量方程

式中：

U'ij、U'ij-1——通道(i,j)和(i,j-1)的有效速度，表示控制體內的平均速度；

fT——湍流動量因子；

v'*——有效比體積；

Aij、Anj——通道(i,j)和(n,j)的橫截面積

K'ij——壓降因子；

gc——單位轉換因子；

g——重力加速度；

Pij、Pij-1——層(i,j)和(i,j-1)處的壓力；

ρij——通道(i,j)的密度

θ——通道與豎直面的夾角；

3)橫向動量方程

式中：

——為層j和j-1上的間隔k的有效速度，即相鄰通道有效速度的代數平均；

sk——子通道劃分線k的長度

lk——相鄰兩個子通道的中心距

KG——橫流摩擦壓降因子；

Pkj-1——間隔k相鄰兩個通道的壓差；4)質量守恆方程

式中：

ECij——質量守恆方程殘差

步驟2：利用Krylov子空間法求解線性化後的子通道方程(2)～(5)，對方程係數矩陣採用壓縮行非零存儲技術CSR存儲，CSR技術採用三個一維數組a、ia和ja來存儲規模大小為m×n的係數矩陣A的非零元素及相應位置。記A矩陣中的非零元素個數為nnz，則：

1)一維數組a，數組長度為nnz，數組元素分別為係數矩陣A中從左到右，從上到下排列的非零元素值；

2)一維數組ia，數組長度為m+1，存儲係數矩陣A中每一行第一個非零元素在總非零元素中的順序，最後一個元素為nnz+1；

3)一維數組ja，數組長度為nnz，存儲係數矩陣A中每一行非零元素在該行中的局部順序。

與現有技術相比，本發明有如下突出優點：

(1)對係數矩陣採用非零存儲技術，避免生成大的係數矩陣，與高斯消去法等直接法相比大大節省計算機內存。

(2)採用Krylov子空間求解子通道計算中的能量、動量和壓力修正方程，與高斯賽德爾迭代、超鬆弛迭代等定點迭代法相比具有較高的計算效率。

附圖說明

圖1是軸向控制容積及變量定義示意圖。

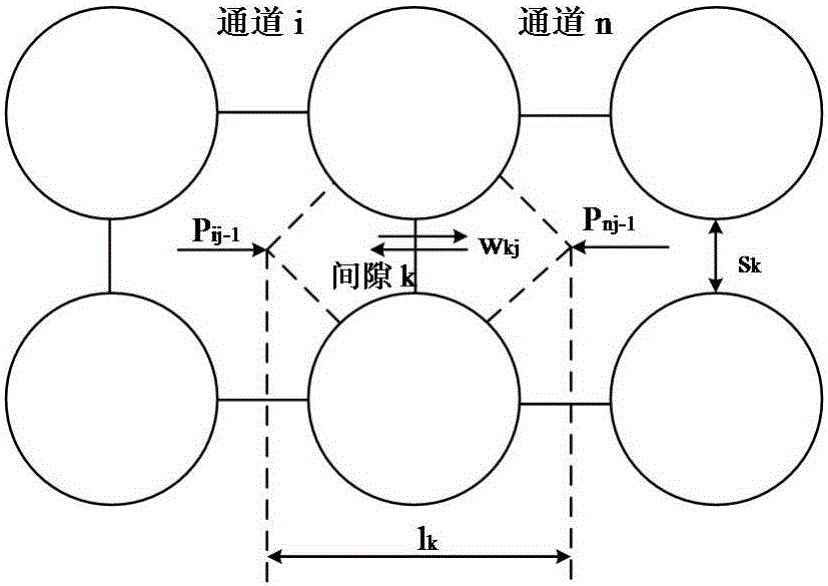
圖2是橫向控制容積及變量定義示意圖。

圖3是典型壓水堆四分之一組件示意圖。

圖4是直接法和GMRES算法求解結果對比示意圖。

具體實施方式

下面結合附圖和具體實施方式對本發明做進一步詳細說明：

對於圖1和圖2中的控制容積，穩態子通道分析求解如下差分形式的穩態守恆方程：

(1)質量守恆方程

控制體(i，j)穩態差分形式的質量守恆方程如下：

(2)能量守恆方程

穩態差分形式的能量守恆方程如下所示：

(3)軸向動量守恆方程

穩態差分形式的軸向動量守恆方程如下：

(4)橫向動量守恆方程

穩態差分形式的橫向動量守恆方程如下：

四個守恆方程(6)～(9)組成了非線性方程組，求解過程為將非線性方程組線性線性化，並且迭代求解。在每個線性化計算中，只求解一個變量，其它變量當作已知量求解。

通過定義式(1)中的三個轉換函數得到(2)～(5)四個線性化的子通道方程。

觀察式(2)可以發現，這是一個係數矩陣為五對角矩陣的線性方程組，通過求解該方程組可以得到焓hij的分布。

同樣可以發現，式(3)是一個係數矩陣為五對角矩陣的線性方程組，通過求解該方程組可以得到焓mij的分布。

軸向和橫向動量方程的求解中假設了壓力場，一個正確的壓力場 應該使計算得到的速度場滿足連續性方程。但據這樣給定的壓力場計算而得的速度場，未必能滿足連續性方程，因此要對給定的壓力場作改進，即進行壓力修正。

根據質量守恆方程，對於控制容積(i，j)，質量守恆殘差可以寫成以下形式：

為了使殘差等於零，根據牛頓迭代法，對壓力場進行修正：

式(11)中，

將式(12)代入式(11)整理可得到線性化後的質量方程式(5)。

通過觀察可見式(5)是係數矩陣為七對角矩陣的線性方程組。

通過子通道守恆方程的推導化簡可發現，能量方程、軸向動量方程、橫向動量方程和壓力修正方程最終求解的都是形如式(13)的線性方程組，當進行全堆芯或者四分之一堆芯的子通道計算時，該線性方程組的係數矩陣A的規模往往很大，達百萬量級，因此合理科學的非零存儲技術以及選取一個穩定高效的線性方程組求解方法對於節 省計算機內存和提高計算效率就顯得尤為重要。

Ax＝b (13)

(1)合理科學的非零存儲技術

採用壓縮行非零存儲技術CSR，CSR技術採用三個一維數組a、ia和ja來存儲規模大小為m×n的係數矩陣A的非零元素及相應位置。記A矩陣中的非零元素個數為nnz，則：1)一維數組a，數組長度為nnz，數組元素分別為係數矩陣A中從左到右，從上到下排列的非零元素值；

2)一維數組ia，數組長度為m+1，存儲係數矩陣A中每一行第一個非零元素在總非零元素中的順序，最後一個元素為nnz+1

3)一維數組ja，數組長度為nnz，存儲係數矩陣A中每一行非零元素在該行中的局部順序；

例如對於大小為4×4的係數矩陣A：

採用CSR技術存儲對應的三個一維數組分別為：

通過非零存儲技術CSR，可以避免存儲係數矩陣A中的零元素，對於大規模的子通道問題，例如全堆芯子通道問題，係數矩陣規模達到百萬量級，CSR技術可以大大節省存儲空間。

(2)穩定高效的線性方程組求解方法

線性方程組的求解方法主要包括直接法、基本迭代法和投影法。常見的直接法有高斯消去法和三角分解法，它們雖然理論簡單便於實現，但是在處理大規模矩陣問題時運算量和所消耗內存太大，無法實用。相比之下，基本迭代法就更適用於高階稀疏對角佔優矩陣的求解，該方法主要包括雅克比迭代法、高斯-賽德爾迭代法和超鬆弛迭代法三類。但是基本迭代法在求解子通道線性化後的方程組效率不高，主要是因為子通道線性化後的方程組的係數矩陣為弱對角佔優矩陣。目前求解該類線性方程組最實用高效的迭代法當屬投影法了。按照投影法的思想，在求解如的線性方程組時，不是直接在n維歐幾裡德空間中尋找解向量，而是在的某一子空間中尋找其近似解：而這個子空間目前主要採用的是Krylov子空間，相應的線性方程組投影法也就被稱為Krylov子空間解法。

對於形如的線性代數方程組，定義初始殘差向量為：

式中：

——解向量的任意迭代初值。

則Rn的m維Krylov子空間可記為：

Krylov子空間解法就是通過利用彼得羅夫-伽遼金條件：

從而在m維仿射子空間中尋找到方程組的近似解的。其中 Lm是另外一個m的子空間。不同的Lm選取方式，產生了不同類別的Krylov子空間解法。最典型的兩種選取方式有：其一，選取 或這類方法主要是基於Arnoldi正交化過程的；其二，選取這類方法主要是基於Lanczos雙正交化過程的，其中AT為矩陣A的轉置。不論如何，Krylov子空間解法實際上是做了這樣一個近似：

式中：

qm-1——m-1階多項式。

顯然，Krylov子空間解法在本質上就是採用一個多項式展開近似。

基於上述Krylov子空間理論的線性代數方程組解法種類眾多，其中比較著名的如共軛梯度法(CG)、Lanczos方法以及廣義極小殘餘方法(GMRES)等。它們各有特點，具體選取哪一種方法要視待解方程組係數矩陣的性質而定。例如CG方法和Lanzos法往往只能用在對稱正定的係數矩陣的求解中；而GMRES方法除了要求係數矩陣非奇異外，幾乎對矩陣性質沒有其它更嚴格的要求。因此，GMRES方法也就成為了當今科學計算領域應用最為廣泛的大型稀疏矩陣線性代數方程組Krylov子空間解法之一。下面將簡要介紹GMRES基本算法。

GMRES算法是基於Arnoldi正交化過程的Krolov子空間解法。它選取了這樣可以使殘差向量對於子空間中的 所有向量都達到極小化，GMRES方法的典型算法如下：

(1)計算

(2)定義(m+1)×m階矩陣並置

(3)對j＝1，2，...，m做

(4)計算

(5)對i＝1，2，...，j做：

(6)

(7)

(8)i循環結束；

(9)如果hj+1，j＝0，則令m＝j，並跳轉至12步；

(10)

(11)j循環結束；

(12)計算且(其中，Vm為以為第i列的n×m階矩陣，為(m+1)×(m+1)階單位陣的第一列)；

(13)結束。

可以證明，完成上述GMRES方法所需的計算量和存儲量是隨著子空間階數m的增加

而分別至少呈O(m2)n和O(mn)增長的。所幸，理論上已證明上述算法所需的子空間階數至多取到n時，迭代就可以收斂。並且在通常的實際應用中，子空間階數m往往是遠遠小於n的，這也就令GMRES方 法更具有了吸引力。但是，對於某些問題，尤其是當矩陣階數很高時，GMRES方法可能需要較高的子空間維數才能獲得滿足精度要求的解，這無疑會帶來更大的計算負擔。目前主要有兩種途徑來解決這個問題：周期性的重啟GMRES算法以及截斷Arnoldi正交化過程。其中相對執行簡單、應用廣泛的當屬前者。以下為典型的重啟GMRES算法：

(1)計算

(2)由向量開始，採用與前述GMRES算法相同的Arnoldi正交化過程，產生Arnoldi正交基Vm及矩陣

(3)計算且

(4)如果解向量滿足精度要求則結束，否則置並跳轉至第1步。

以上為每m步迭代實現一次重啟的GMRES算法。

分別採用高斯消去法和GMRES法求解圖3所示的典型壓水堆四分之一組件和全組件，計算所需時間對比如圖4所示，可以看到隨著計算問題規模的增大，GMRES的加速效果越顯著。