一種基於噪聲功率的圓陣的DOA估計方法與流程

2023-11-11 05:08:47 1

本發明屬於無線通信技術領域，尤其涉及一種在無線多輸入多輸出(Multiple Input Multiple Output，MIMO)通信系統中利用噪聲來進行對信號真實子空間估計的算法。

背景技術：

信號處理領域的一個重要分支——陣列信號處理在生物醫學工程民用通信、軍事電子戰等諸多方面有著廣泛的應用。目前，陣列信號處理大致分為兩個主要研究方向：自適應空域濾波與空間譜估計。

首先陣列對信號進行處理在現代通信中具有很好的應用前景，並且在近些年中得到了迅猛的發展。隨著人們對通信系統的容量和質量的不斷提出更高的標準，普通的通訊天線已經不能完全滿足越來越高的性能指標要求。因此，這就要求我們有必要採取一些技術手段和方法將天線其他的潛能全部發掘，從而形成滿足現代通信需求的天線系統。那麼為了滿足現代通信系統對容量和質量不斷提高的要求，陣列天線的設計也就成為了一種流行的方法。由於通訊需求的不同，那麼就需要不同形狀的陣列結構來滿足不同的波束覆蓋形式。我們知道圓錐或圓環陣等共形陣具有360方位角度的覆蓋能力，它們可以形成一個全向的波束、多個波束或是一個窄波束並且都可以被導向360方位角度。並且能實現半球覆蓋陣列天線系統在移動通信基站天線的應用中將日益凸顯它的魅力。另外，一些通信衛星也開始採用共形陣作為天線。

最早的基於陣列的DOA算法為常規波束形成(CBF)法，也稱為Barlett波束形成法。這種方法是傳統時域傅立葉譜估計方法中的一種空域簡單拓展形式，即用空域各陣元接收的數據代替傳統時域處理中的時域數據。與時域傅立葉限制一樣，將這種方法擴展至空域後，陣列的角度分辨力同樣受到空域「傅立葉限」的限制。空域「傅立葉限」就是陣列的物理孔徑限，常稱「瑞利(Rayleigh)限」。換句話說，對位於一個波束寬度的空間目標不可分辨。所以，提高空域處理精度的有效方法就是增大天線孔徑(等效於見笑波束寬度)，從而達到提高精度的目的。但對於許多實際應用環境而言，增大天線孔徑是不現實的，所以需要更好地算法來提高方位估計的 精度。因此，在CBF方法提出之後許多時域非線性譜估計方法都相繼被應用於空域信號的處理之中，產生了所謂「高解析度譜估計方法」，具有代表性的有：Pisarenko的諧波分析法，Brug的最大熵法，Capon的最小方差法等。在隨後的研究中，不同的學者提出了不同的方法和理論來突破陣列信號處理的瑞利限。

二十世紀七十年代末，美國的Schmidt-R-O等人提出了多重信號分類算法(MUSIC)，這種算法成功突破陣列信號處理的瑞利限，向現代超解析度測向技術邁出了重要一步。MUSIC算法的出現同時也標誌著特徵子空間算法的興起。子空間測向算法的共同特點就是通過對陣列接收數據矩陣的數學分解(特徵分解，奇異值分解，QR分解等)，將接收數據分解為兩相互正交子空間。這兩個子空間中與陣列流形空間一致的稱為信號子空間，另一個與信號子空間正交的稱為噪聲子空間。子空間分解算法即利用兩子空間相互正交的特性構成空間譜，通過譜峰搜索完成測向工作。此外，作為一種具有代表性的子空間方法，ESPRIT算法也隨後被提出且得到了廣泛的研究。

從20世紀80年代後期開始，這個領域又出現了一類子空間擬合類算法，其中比較有代表性的算法有最大似然(ML)算法、加權子空間擬合(WSF)算法及多維MUSIC算法等。最大似然(ML)參數估計類方法是參數估計理論中一種典型和實用的估計方法，它包括確定性最大似然算法(DML)和隨機性最大似然算法(SML)。1988年，Ziskind L與Max M討論了將最大似然參數估計方法應用于波達方向估計，由於方向估計似然函數是非線性的，求解其最優解需進行多維搜索，運算量巨大。因此後續研究集中在算法的估計性能和實現上。

為了更好地進行空域濾波，我們可以先對信號進行空間譜估計，它與自適應陣列技術不同，空間譜估計的側重研究方向是空間多傳感器陣列所構成的處理系統對感興趣的空間信號的多種參數進行準確估計的能力，所以該系統主要目的是估計信號的空域參數或信源位置，這也是雷達、通信、聲納等許多領域的重要任務之一。空間譜估計技術可以大大改善在系統處理帶寬內空間信號的角度估計精度、角度分辨力及其他相關參數精度，因而其應用前景十分廣泛。

技術實現要素：

為了克服普通DOA估計時開銷過大的缺陷，本發明提出一種基於噪聲功率估計信號子空間的DOA估計算法。利用高斯白噪聲功率不變的特性，將子空間DOA估計方法由單純分離信號子空間與噪聲子空間變成了通過利用噪聲的存在分離出 信號子空間與噪聲子空間，從而利用矩陣理論的相關理論，在信道較差的情況下將性能提高50％。

為了方便地描述本發明的內容，首先對本發明中所使用的概念和術語進行定義。

波達方向(DOA)估計：確定同時處在空間某一區域內多個感興趣的信號的空間位置(即多個信號到達陣列參考陣元的方向角)。

信號子空間：由信號導向矢量線性組合而成的空間組合。

噪聲子空間：由非信號導向矢量線性組合而成的空間組合。

信噪比：信號功率與噪聲功率的比值。

首先一種傳統子空間DOA估計算法如下所示：

假設目標信號源是相互統計獨立的，並且加性高斯白噪聲是它接收到的噪聲。那麼可以得出信號相關矩陣P可以被表示為P＝E[s(n)sH(n)]＝diag{Pi}。其中，Pi為第i個信號的平均功率。類似的，可以定義接收信號x(n)的相關矩R為：R＝E[x(n)xH(n)]＝APAH+σ2I，其中，σ2表示加性高斯白噪聲的方差。為了保證方向矩陣A的各列線性獨立，所以N＞L，也就是說陣元數必須大於信號源數。

上式的形式與MUSIC算法中信號的自相關矩陣有著完全相同的形式，並且信號的頻率矩陣的形式也與方向矩陣A完全相同，所以可以將MUSIC算法應用於空間相關矩陣的處理當中，來估計矩陣A中蘊含的相位信息，進一步的由可以估計出信號源的方向角，從而完成對信號的波達方向估計。

為求得目標信號的相位信息，將對相關矩R進行特徵值分解，並將特徵值按單調非遞增順序排列，那麼前L個特徵值對應的歸一化特徵向量就將張成信號子空間，後N-L個向量張成噪聲子空間。

若定義噪聲子空間為G＝uK+1，uK+2，…，uK+N，則其與陣列流形A滿足如下關係AHG＝0，即，信號的每一個陣列導向向量在信號為非相干信號的條件下都與噪聲子空間正交。在通常情況下，通過M次快拍得到的接受數據x(n)的時間平均估計來替代原相關矩，設其為。通常的SVD分解產生的噪聲子空間並不與陣列流形嚴格正交，故利用這一條重要性質，構造譜峰搜索函數如下：其中，θ∈(-90°,90°)。MUSIC譜P的L個峰值位置對應的就是信號的波達方向θk的估計。

一種基於噪聲功率的圓陣的DOA估計方法，具體步驟如下：

S1、利用陣列接收的N次快拍數據利用計算得到信號的空間相關矩R；

S2、對進行特徵值分解，得到噪聲子空間矩陣G；

S3、根據S1所述空間相關矩R和S2所述噪聲子空間矩陣G進行譜峰搜索，得到其譜峰位置，從而得到波達方向估計值。

本發明的有益效果是：

本發明在信道較差的情況下將性能提高50％。

附圖說明

圖1基於圓陣的DOA估計算法系統圖。

圖2是天線訓練過程中的一次測量圖。

圖3是本發明仿真程序的流程圖。

圖4是入射角為(36°,20°)時的20次測量值。

圖5是入射角為(45°,30°)時的20次測量值。

圖6是入射角為(30°,45°)時的20次測量值。

具體實施方式

下面結合附圖，對本發明作進一步地詳細描述。

首先，通過對接收信號進行自相關得到Rxx，假設目標信號源是相互統計獨立的，並且加性高斯白噪聲是它接收到的噪聲。那麼可以得出信號相關矩陣P可以被表示為P＝E[s(n)sH(n)]＝diag{Pi}。其中，Pi為第i個信號的平均功率。類似的，可以定義接收信號x(n)的相關矩R為：R＝E[x(n)xH(n)]＝APAH+σ2I。

然後，得到第一個由真實信號子空間線性組合而成的向量對於假設信源之間是不相關的，並且如果 是期望方向的導向矢量的時候，下式可以被得到：

，其中，是由被預處理後的所有導向矢量線性組合而成的，即，只由通過預處理後的信號子空間線性組合而成的K階向量。

當不是期望方向的導向矢量的時候，則：

其中，當不是期望方向的導向矢量的時候，在有噪聲存在的時候是所有與處理後的導向矢量與導向矢量的線性組合，即，包含真實信號子空間與另一空間的K+1階向量，。當噪聲不存在的時候，不論期望方向是否為期望方向的導向矢量，得到的結果都只是由全部信號子空間向量線性組合而成的K階向量，所以在這個算法可以在信噪比較小的時候成立，並且需要滿足LHL＝I，因為只有這樣，在經過與處理之後在空間中的噪聲依然保持高斯白噪聲形式。

求出其他子空間向量，由於不論是否使用期望方向的導向矢量都包含整個真實信號子空間。所以可以根據下式得到第二個包含真實信號子空間導向矢量的向量：

通過對矩陣理論中學習，可以得到上述方程最優解是：

要迭代得出剩餘(K-1)個正交向量，定義兩個中間向量：

其中，是前n-1個輔助矢量基線性組合而成的，則

其中，

根據公式並運用數學歸納法最終可以求得：

其中，p的範圍是[1,K-1]，即如果是期望方向的導向矢量的時候，矢量基是K階，如果有第K+1個向量與這K個相互正交的向量正交，那麼這個向量一定是零向量。當不是期望方向的導向矢量的時候，那麼因為這個矢量基是K+1階，所以這個向量不是零向量。

將第K+1個正交向量表達出來：

在表達出第K+1個輔助矢量積後，如果是期望方向的導向矢量的時候， 所以可以直接用來進行譜峰搜索。從式子中可以分析得出即使是有噪聲存在的情況下但是他也會非常接近於零，那麼它的倒數在也會在該點形成一個波峰。

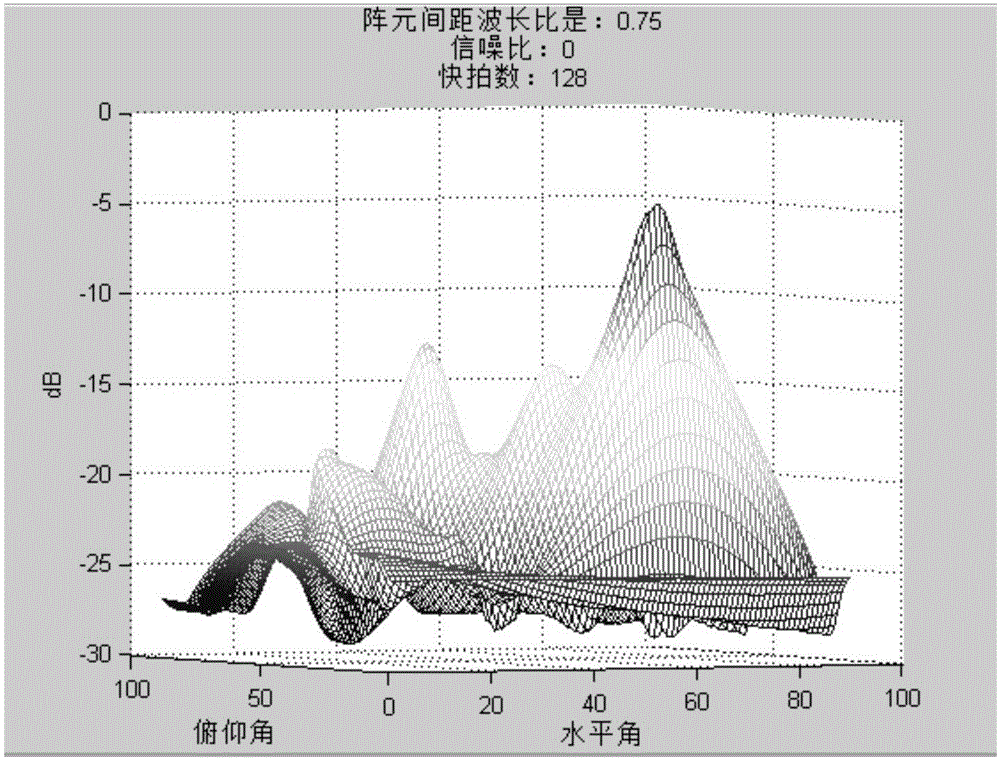
當入射角為3個時分別是：(60°,45°)(60°,20°)(45°,30°)，matlab運用上述算法仿真如圖2所示，在仿真中採用了25個陣元，相模數值等於10，並且陣元間距是0.75個波長，信噪比是0dB,快拍數是128。

將就該算法與經典高解析度算法MUSIC算法相比較，首先將分別假設他們的入射角為：(36°,20°)(30°,45°)(45°,30°)，經過20次仿真，在仿真中採用了25個陣元，相模數值等於10，並且陣元間距是0.75個波長，信噪比是0dB,噪聲採用的是高斯白噪聲，快拍數是200的模擬來進行仿真。得出的數據然後做折線圖如圖4，圖5和圖6所示：

從圖4，圖5，圖6中可以看出，在精度是1度的情況下，同時快拍數為200，信噪比是0dB時，用基於均勻圓陣的輔助矢量基DOA估計算法測量出來的角度與真實值差距一般是1度。