基於同步壓縮短時傅立葉變換的盲分離混合矩陣估計方法與流程
2023-06-03 19:56:41
本發明涉及機械振動信號和聲輻射信號處理領域,具體涉及一種基於同步壓縮短時傅立葉變換的盲分離混合矩陣估計方法。
背景技術:
機械系統的振動和噪聲對系統的性能與安全有重要影響,如潛艇推進系統振動過大容易被敵方發現且幹擾自身的聲吶探測,火箭發動機振動過大容易導致其攜帶的衛星及儀器不能正常工作等。因此,尋找振動噪聲源並採取措施減小其影響至關重要。傳感器檢測的觀察信號往往是多個振動源疊加,而且鑑於機械系統的複雜性,通常缺乏振動源混合特性的先驗知識,給振動噪聲源的尋找帶來了挑戰。盲源分離能夠在未知源信號和混合方式的情況下,對源信號進行估計,很好地解決了以上難題。
然而,在工程實際中,傳感器的數目經常會少于振動源的數目,如下面幾種情況:(1)傳感器安裝數目較少,某些裝備不能隨意安裝傳感器,如火箭和飛彈等一旦型號確定,不能隨意更改結構方案;(2)傳感器長期工作在惡劣環境中引起故障,沒有採集到數據,在數據缺失的情況下,重新採集數據費時費力;(3)數據可用性差,傳感器安裝的位置不合理,對信號振動不敏感。此時,傳感器採集的觀測信號數目少於源信號數目,屬於欠定情況,傳統的盲源分離方法(如快速獨立分量分析,自然梯度算法等)效果較差,因此研究在欠定情況下混合矩陣的估計方法具有重要的學術意義和工程價值。
目前,欠定情況下混合矩陣的估計方法主要利用信號在時域、頻域以及時頻域的稀疏性提取單源點,進而對單源點進行聚類分析,可以得到對應於每個源的單源點,即對應於混合矩陣的每一列。然而對於機械系統而言,很難保證所有的振動信號在時域和頻域上均具有稀疏性,而基於時頻域的混合矩陣估計方法又多為基於stft和小波變換等,這些傳統時頻處理方法得到的時頻變換能量聚集性低,造成複雜機械信號在時頻域上稀疏性不足,進而導致單源點估計具有較大誤差,在低信噪比條件下,甚至不能正確估計混合矩陣。
技術實現要素:
為了解決現有技術中的問題,本發明提出一種基於同步壓縮短時傅立葉變換的盲分離混合矩陣估計方法,能夠提高觀察信號時頻域的稀疏性,提高了有用信號的能量,進而減弱噪聲的影響,正確估計混合矩陣。
為了實現以上目的,本發明所採用的技術方案為:包括以下步驟:
步驟1,將所有待分析的觀察信號進行短時傅立葉變換得到相應的時頻域復矩陣;
步驟2,將獲取的時頻域復矩陣對時移因子求偏導,並與時頻域復矩陣取比值,得到瞬時頻率估計算子矩陣,利用瞬時頻率估計算子矩陣對時頻域復矩陣在頻率方向上進行積分重排,實現時頻域能量重排至能量重心,得到時頻域復矩陣的同步壓縮時頻矩陣;
步驟3,利用稀疏編碼技術在同步壓縮時頻矩陣中尋找來自同一個1-d子空間的時頻點,構造一個基於l1範數的目標函數,實現單源點快速提取;
步驟4,將已提取的單源點進行層次聚類,得到所有類的聚類中心,每個聚類中心對應混合矩陣的一列,進而利用聚類中心的方向實現對混合矩陣的估計。
所述步驟1中對每個待分析的觀察信號進行短時傅立葉變換,對第i個待分析的觀察信號xi=[xi1xi2…xin]進行短時傅立葉變換得到對應的時頻域復矩陣為:
其中i=1,2,…,m,n表示採樣點個數,在時頻域復矩陣中,行表示頻率,列表示時間,表示的第k列,k=1,2,…,k。
所述步驟2中採用同步壓縮變換對時頻域復矩陣進行後處理,首先將時頻域復矩陣對時移因子求偏導;
然後得到的偏導與時頻域復矩陣本身取比值,得到瞬時頻率估計算子矩陣其中,i=1,2,…,m,表示將時頻域復矩陣對其時移因子u求偏導,為虛數單位,
最後利用瞬時頻率估計算子矩陣ωi對時頻域復矩陣在頻率方向上進行積分,得到時頻域復矩陣的同步壓縮時頻矩陣:yi=[yi,1yi,2…yi,k],其中i=1,2,…,m,yi,k表示yi的第k列。
所述步驟2中對同步壓縮時頻矩陣yi進行重新排列,使得每個yi轉換成一個行向量,即其中i=1,2,…,m,t表示轉置,則所有觀察信號的同步壓縮時頻矩陣組合成矩陣:
所述步驟3中同步壓縮時頻矩陣yi的每一列是由不同的觀察信號在同一時頻點的複數值組成的列向量,對應於觀察信號在此時頻點的方向,令其中為的第q列,q=1,2,…,q,則利用中的其他列進行稀疏編碼,即s.t.cii=0,其中為編碼係數。
所述步驟3中若某一時頻點為單源點,則此時頻點的編碼係數中只有一個元素非零,即同一個源對應的單源點所對應的時頻列向量位於同一個1-d子空間中,則對l0範數進行優化尋找單源點,在ci足夠稀疏時,l0範數優化與l1範數優化等價,l0範數為:min||ci||0,s.t.cii=0,l1範數為:min||ci||1,s.t.cii=0。
所述步驟3基於l1範數建立如下目標函數:
s.t.cii=0
利用該目標函數尋找與編碼係數ci只有一個元素為非零值相對應的矩陣中的列向量,則該列向量對應的時頻點為單源點,其中λ是正則化參數。
所述尋找與編碼係數ci只有一個元素為非零值優化為:|cij|>ε1,cip<ε2且cii=0,其中ε1和ε2表示設定的閾值,i≠j,i≠p且j≠p。
所述步驟4中採用下列公式評價估計的混合矩陣的準確性:
其中,ai為原始混合矩陣a的第i列,為估計的混合矩陣對應的第i列,e為準確性指標,代表估計的混合矩陣和原始混合矩陣的相近程度。
與現有技術相比,本發明利用stft同步壓縮方法將待分析信號從時域變換到時頻域,極大地提高了待分析信號在時頻平面的能量聚集性,從而提高其在時頻域的稀疏性。作為本方法的前處理,同步壓縮短時傅立葉變換具有較強的魯棒性。因此本方法相比將傳統時頻分析作為前處理的方法,能夠得到具有更強的魯棒性的結果。本發明在提取單源點的過程中,利用稀疏編碼技術,尋找編碼係數中只有一個元素非零對應的時頻點,實現位於同一個1-d子空間的時頻點的搜尋。通過最小化編碼係數的l1範數,構造一個誤差最小目標函數實現單源點的提取,能夠進一步增強對噪聲的抑制作用,最後通過層次聚類法實現混合矩陣的估計。本發明僅需觀察信號大於等於2個,即可實現任意源數目混合矩陣的估計,並且當信噪比較低時,仍然保持良好的估計性能,具有較好的魯棒性。
附圖說明
圖1為實施例1的仿真信號波形圖;
圖2為本實施例1的仿真信號的stft時頻圖;
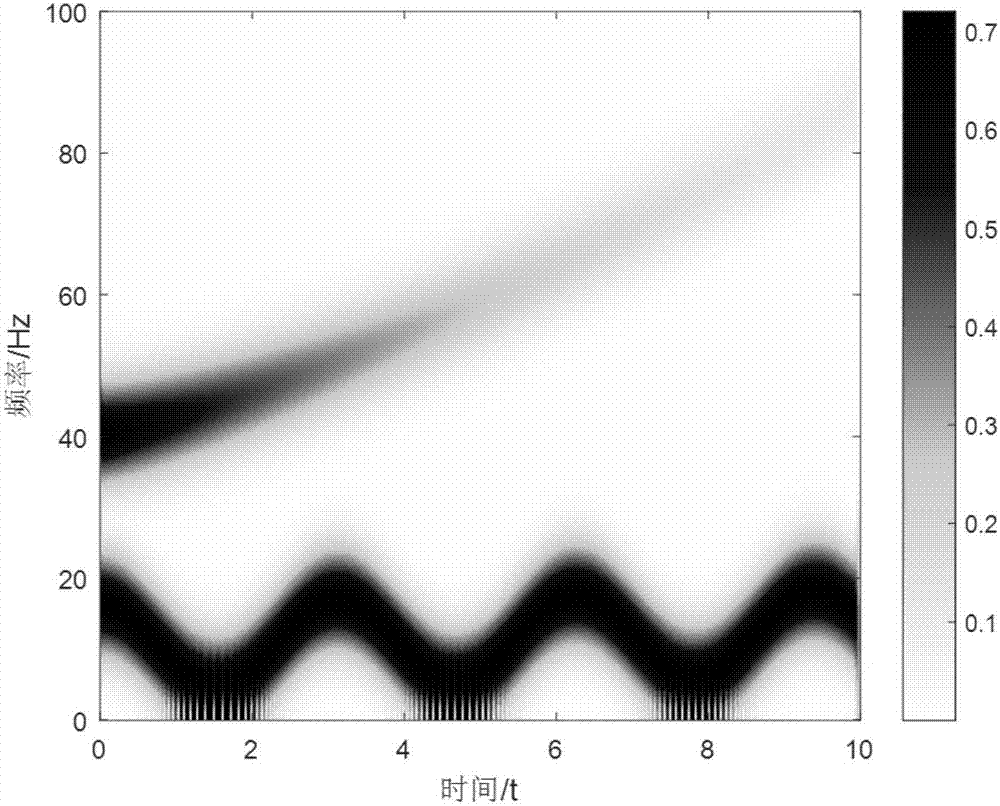
圖3為實施例1的仿真信號的stft同步壓縮時頻圖;
圖4為實施例2的六個源信號波形圖;
圖5為實施例2的六個源信號經過混合矩陣後得到的兩個觀察信號的混合信號波形圖;
圖6為實施例2不同信噪比下混合矩陣估計誤差對比圖;
圖7為實施例2不同信噪比下時間消耗對比圖;
圖8為實施例2不同單源點數量不同信噪比下混合矩陣估計誤差對比圖;
圖9為實施例2不同單源點數量不同信噪比下時間消耗對比圖。
具體實施方式
下面結合具體的實施例和說明書附圖對本發明作進一步的解釋說明。
本發明包括以下步驟:
步驟1,將待分析的觀測信號x進行短時傅立葉變換得到相應的時頻域復矩陣
對每個待分析觀察信號xi(t)依次進行短時傅立葉變換操作,其中x(t)=[x1(t)x2(t)…xm(t)]t為所有觀察信號,xi(t)表示x(t)的第i個觀察信號,m表示觀察信號的個數;對第i個待分析的觀察信號xi=[xi1xi2…xin]進行短時傅立葉變換得到對應的時頻域復矩陣其中i=1,2,…,m,n表示採樣點個數,在中,行表示頻率,列表示時間,表示的第k列,k=1,2,…,k;
步驟2,將獲取的時頻域復矩陣對時移因子求偏導,並與取比值,得到瞬時頻率估計算子矩陣ωx,利用ωx對在頻率方向上進行重排,實現時頻域能量重排至能量重心,得到的同步壓縮時頻矩陣y,提高x在時頻域上的稀疏性;
採用同步壓縮變換對步驟1中得到的時頻域復矩陣進行後處理,將對時移因子求偏導,再與本身取比值,得到瞬時頻率估計算子其中i=1,2,…,m,表示將對其時移因子求偏導,為虛數單位,
利用得到的瞬時頻率估計算子ωi對在頻率上進行積分,得到同步壓縮後的復矩陣,即為的同步壓縮變換yi=[yi,1yi,2…yi,k],其中i=1,2,…,m,yi,k表示yi的第k列;
將得到的yi進行重新排列,使得每個yi轉換成一個行向量,即其中i=1,2,…,m,t表示轉置,則所有觀察信號的同步壓縮變換組合成一個矩陣
步驟3,利用稀疏編碼技術,將單源點的尋找轉化為尋找來自同一1-d子空間的時頻點的問題,構造一個基於l1範數的目標函數,實現單源點快速提取;
同步壓縮變換矩陣的每一列是由不同的觀察信號在同一時頻點的複數值組成的列向量,對應於觀察信號在此時頻點的方向,令其中為的第q列,q=1,2,…,q,則可以被中的其他列進行稀疏編碼,即s.t.cii=0,其中為編碼係數;
若某一時頻點為單源點(在此時頻點上僅存在一個源),則此時頻點的編碼係數中只有一個元素非零,即同一個源對應的單源點所對應的時頻列向量位於同一個1-d子空間中,則尋找單源點的問題轉化為以下l0範數優化問題:min||ci||0,s.t.cii=0,此優化問題在ci足夠稀疏時,與下述的l1範數優化問題等價:min||ci||1,s.t.cii=0;
為了提高本方法的穩定性和魯棒性,構造如下目標函數:s.t.cii=0,尋找與編碼係數ci只有一個元素為非零值相對應的中的列向量,其中λ是正則化參數,則該列向量對應的時頻點為單源點,考慮到噪聲的影響,尋找編碼係數ci只有一個元素為非零值優化為|cij|>ε1,cip<ε2且cii=0,其中ε1和ε2表示設定的閾值,i≠j,i≠p且j≠p;
步驟4,將已提取的單源點進行層次聚類,得到估計的聚類中心,每個類的中心對應混合矩陣的一列,進而利用聚類中心的方向實現混合矩陣的估計;
利用步驟3的單源點進行層次聚類,可獲得所有類的聚類中心,每個聚類中心與混合矩陣的某一列相對應,通過聚類中心的方向可得到混合矩陣每列的估計,從而得到估計的混合矩陣
為了評價本方法估計混合矩陣的準確性,利用下面的性能指標:
其中ai為原始混合矩陣a的第i列,為估計的混合矩陣對應的列,e為準確性指標,代表估計的混合矩陣和原始混合矩陣的相近程度,即估計的準確性。
實施例1,為了說明同步壓縮變換相對於傳統時頻變換的優越性,選取一個仿真信號,其波形圖如圖1所示。仿真信號的表達式為:f(t)=cos{2π[0.1t2+3sin(2t)+10t]}+e-0.2tcos[2πt(40+t1.3)],採樣時間為10s,採樣頻率為200hz。從表達式中看出其由兩部分組成,一部分的頻率為0.1t+[3sin(2t)]/t+10,另一部分的頻率為40+t1.3,兩部分的頻率都隨著時間的變化而變化。
將該仿真信號進行stft變換,得到的時頻圖如圖2所示,其頻率為兩部分,但是由於時頻聚集性不高,可讀性不強。
圖3所示為該仿真信號經過stft同步壓縮變換得到的時頻圖,與圖2相比,時頻聚集性得到明顯提高,而且由於頻率上的能量重排,增加了有用信號的能量。與圖2相比,圖3中的最大能量由0.7增加到了4。與單獨的stft相比,stft同步壓縮變換極大地提高了時頻平面的稀疏性。
實施例2,選擇6個語音信號作為源信號,其波形圖如圖4所示,雖然時域上有一定的稀疏性,但是6個語音信號在大部分時間內重疊,即在大多數時間點存在多個語音信號。選擇原始混合矩陣如下:a=[0.2588,0.7071,0.9659,0.9659,0.7071,0.2588;-0.9659,-0.7071,-0.2588,0.2588,0.7071,0.9659]。
圖5所示為實施例2中6個語音信號經過原始混合矩陣a後得到的兩個觀察信號,即,此時相當於共有2個傳感器,而源信號的個數為6,為欠定盲源分離情況,一般的超定或者適定盲源分離分離方法失效。
在snr=40db,窗長為1024,窗每次移動512採樣點條件下,利用本方法估計的混合矩陣為:和原始混合矩陣相比,估計混合矩陣與其絕對差值為:每個元素的絕對誤差均小於0.05,表明本方法具有良好的估計性能。
為了評價本發明方法估計混合矩陣的性能,利用下述指標:
其中ai為原混合矩陣a的第i列,為本方法估計混合矩陣對應的列。
圖6所示為實施例2中本發明方法在不同信噪比條件下的誤差對比圖,其參數如下:窗長為1024,窗每次移動採樣點數為512,每個數據均為相同參數下重複10次得到的平均值。圖6表明在不同的信噪比下,算法的性能誤差均小於0.03,表明本方法對噪聲具有較好的魯棒性。
圖7為實施例2中本方法在不同信噪比條件下所消耗的時間對比,參數和圖6相同,顯示每次消耗的時間在4s~6s,表明了本方法的高效性。
圖8所示為實施例2中提取不同的單源點數量在不同的信噪比下誤差對比圖,參數和圖6相同,表明隨著單源點數量的增加,本方法的誤差減小,而單源點數量增加到一定數量後,單源點數量對誤差的影響減小,但是在低信噪比條件下,單源點數量的增加,誤差反而有略微的增大。
圖9所示為實施例2中提取不同的單源點數量在不同的信噪比下消耗時間對比圖,參數和圖6相同,表明隨著單源點數量的增加,本方法消耗的時間逐漸增加,一方面是由於提取單源點數量增加導致的,另一方面是由於單源點數量增加,在聚類時也需要消耗更多的時間。通過大量的試驗和仿真驗證,單源點的數量在300~1000時,本方法即可具有較高的運算效率,並且具有較小的估計誤差。
本發明通過對觀察信號進行stft同步壓縮變換,使之由時域變換到時頻域,通過在頻率上重排各時頻點的能量,極大地提高了待分析信號在時頻平面的能量聚集性,從而提高時頻域的稀疏性並減弱噪聲的影響。在提取單源點的過程中,利用稀疏編碼方法,尋找編碼係數中只有一個元素非零對應的時頻點,實現位於同一個1-d子空間的時頻點的搜尋。通過最小化編碼係數的l1範數,構造一個誤差最小目標函數實現單源點的提取,進一步增強了對噪聲的抑制作用,最後通過層次聚類法實現混合矩陣的估計。本方法是一種新的欠定盲源分離混合矩陣估計方法,僅需觀察信號大於等於2個,即可實現任意源數目混合矩陣的估計,並且當信噪比較低時,仍然保持良好的估計性能,具有較好的魯棒性,為實際振動噪聲源分離提供有效支持。
