一種面向GPDSP的反卷積矩陣的向量化實現方法與流程
2023-05-26 13:40:34 1
本發明主要涉及到向量處理器及機器學習領域,特指一種面向gpdsp的反卷積矩陣的向量化實現方法。
背景技術:
深度學習(deeplearning,dl)是當前機器學習領域的一個重要研究方向。dl通過構造多層感知器(multilayerperception,mlp)來模擬人腦的分層感知方式,mlp能夠通過組合低層次特徵來表達屬性類別或高層的抽象特徵,從而成為當前目標識別領域的研究重點。
經典的dl模型主要包括自動編碼機模型(autoencode,ae)、深度信念網絡模型(deepbeliefnetworks,dbns)及卷積神經網絡模型(convolutionalneuralnetworks,cnn)。一般來說,上述模型主要通過編碼器從輸入圖像中提取特徵,從底層逐層向上將圖像轉化到高層特徵空間,相應的,使用解碼器將高層特徵空間的特徵通過網絡自頂向下重構輸入圖像。其中,深度學習模型主要分為無監督學習模型和有監督學習模型,自動編碼機和深度信念網絡就是無監督學習模型的代表,它們可以自底向上地逐層學習豐富的圖像特徵並為高層次應用,如圖像識別、語音識別等。而cnn模型則是有監督的學習模型,通過構建卷積層及池化層來構建多層的卷積神經網絡,通過bp(backpropogation)算法反向調整濾波模板,經過多次的正向計算和反向調優來構建具有高識別率的神經網絡。
由於cnn模型涉及到大量的矩陣操作,如,矩陣與矩陣乘法、矩陣與向量乘法、向量與向量乘法、矩陣與矩陣卷積、矩陣擴充、矩陣反卷積以及各種超越函數的計算,使得cnn模型需要佔用大量的計算資源。通過對cnn模型的深入分析發現,該模型中涉及大量的數據並行性,目前運行cnn模型的硬體平臺主要有cpu、gpu、fpga及專用的神經網絡處理器,如中科院計算所的寒武紀系列。
通用計算數位訊號處理器(general-purposedigitalsignalprocessor,gpdsp)一般包括cpu核和dsp核,cpu核主要負責包括文件控制、存儲管理、進程調度、中斷管理任務在內的通用事務管理及對通用作業系統的支持;dsp核主要包含若干具有強大計算能力的浮點或定點向量處理陣列,用於支持高密度的計算任務,向量處理器一般由n個處理單元(pe)組成,每個pe包含若干個功能單元,一般包括alu部件、加法部件、移位部件等,這些部件可以讀寫一組局部寄存器,每個處理單元包含一組局部寄存器,所有處理單元同一編號的局部寄存器在邏輯上又組成了一個向量寄存器。向量處理器採用simd的方式,n個處理單元在同一條向量指令的控制下同時對各自的局部寄存器進行相同的操作,以開發應用程式的數據級並行性。
技術實現要素:
本發明要解決的技術問題就在於:針對現有技術存在的技術問題,本發明提供一種原理簡單、操作方便、能充分利用向量處理器完成特殊數據計算、縮短整個算法運行時間、提高算法執行效率的面向gpdsp的反卷積矩陣的向量化實現方法,用以滿足計算密集型應用的需求。
為解決上述技術問題,本發明採用以下技術方案:
一種面向gpdsp的反卷積矩陣的向量化實現方法,其特徵在於,由gpdsp的cpu核為卷積神經網絡中前向傳播階段產生的權值矩陣及反向計算階段的殘差矩陣分配相應的標量存儲空間和向量存儲空間,其步驟為,
s1:設殘差矩陣a(m,m)、權值矩陣b(n,n)及反卷積結果矩陣c(m+n-1,m+n-1),且m>n;
s2:通過控制循環次數,首先計算反卷積結果矩陣c前n-1行元素;
s3:固定循環次數,計算反卷積結果矩陣c第n行至第m行元素;
s4:通過控制循環次數,計算反卷積結果矩陣c倒數第n-1行至倒數第1行元素。
作為本發明的進一步改進:所述權值矩陣b置於標量存儲體,反卷積矩陣a置於向量存儲體,且權值矩陣b從後至前,倒序來取。
作為本發明的進一步改進:所述步驟s2的詳細步驟為:
s2.1取權值矩陣b第n行的最後一個元素,bn-1,n-1,取殘差矩陣a第一行元素,將bn-1,n-1廣播至標量寄存器中的元素與矩陣a第一行元素對應相乘,累加上將bn-1,n-2向量化後與移位後的殘差矩陣a的第一行元素一一對應相乘的結果;重複以上步驟n次,n位權值矩陣b列數,完成反卷積結果矩陣c第一行元素的計算;
s2.2順移至殘差矩陣a的第二行元素,計算過程如步驟2.1,循環n+n次完成反卷積結果矩陣c第二行元素的計算;
s2.3順移至殘差矩陣a的第n-1行元素,計算過程如步驟2.1,循環(n-1)*(n-1)次完成反卷積結果矩陣c第n-1行元素的計算。
作為本發明的進一步改進:所述步驟s3中,反卷積結果矩陣c的第n行至第m行的每一行元素的計算都在步驟s2.3的基礎上順移至殘差矩陣a的第n行,計算過程如步驟2.1,循環n*n次完成反卷積結果矩陣c中間某一行行元素的計算。
作為本發明的進一步改進:所述步驟s4的詳細步驟為:
s4.1倒數第n-1行元素由權值矩陣b的前n-1行元素參與計算,計算過程如步驟s2.3;
s3.3倒數第2行元素由權值矩陣b的前2行元素參與計算,計算過程如步驟s2.2;
s3.4倒數第1行元素由權值矩陣b的前1行元素參與計算,計算過程如步驟s2.1。
與現有技術相比,本發明的優點在於:
1、本發明的面向gpdsp的反卷積矩陣的向量化實現方法,將卷積神經網絡反向計算中涉及到的殘差矩陣a(m,m)和權值矩陣b(n,n)反卷積至輸入空間,即,反卷積結果矩陣c(m+n-1,m+n-1),不僅避免了數據的搬移、矩陣的擴充,且能充分利用向量處理器中多個並行處理單元能夠同時進行相同運算的特點來進行大量的同類型操作,使用特殊的vshufw指令,大大提高數據的復用率,進而大幅度提高反卷積矩陣的計算效率。
2、採用本發明的方法比傳統的方法更加簡單高效,目標向量處理器實現的硬體代價低,在實現相同功能的情況下,降低了功耗。另外,本發明的方法,實現簡單、成本低廉、操作方便、可靠性好。
附圖說明
圖1是本發明方法的流程示意圖。
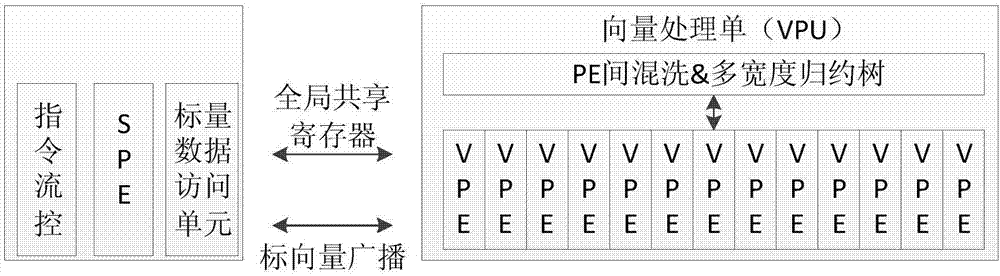
圖2是本發明面向的gpdsp的簡化結構模型示意圖。
圖3是本發明中的反卷積計算流程示意圖。
圖4是本發明在具體應用實例中反卷積結果矩陣第1行元素計算示意圖。
圖5是本發明在具體應用實例中反卷積結果矩陣第2行元素計算示意圖。
具體實施方式
以下將結合說明書附圖和具體實施例對本發明做進一步詳細說明。
假設c=a*b,即矩陣a和矩陣b的卷積是c,也就是說已知a和b求c的過程叫做卷積,那麼如果已知c和a或者c和b求b或a的過程就叫做反卷積。如圖2所示,為本發明所面向的gpdsp的簡化結構模型示意圖。
如圖1和圖3所示,本發明的面向gpdsp的反卷積矩陣的向量化實現方法,其步驟為:
s1:反卷積結果矩陣c前n-1行元素的計算;
s1.1由gpdsp的cpu核為卷積神經網絡中前向傳播階段產生的權值矩陣及反向計算階段的殘差矩陣分配相應的標量存儲空間和向量存儲空間;
s1.2設殘差矩陣a(m,m)、權值矩陣b(n,n)及反卷積結果矩陣c(m+n-1,m+n-1),且m>n;
s1.3取權值矩陣b第n行的最後一個元素,bn-1,n-1,取殘差矩陣a第一行元素,將bn-1,n-1廣播至標量寄存器中的元素與矩陣a第一行元素對應相乘,累加上將bn-1,n-2向量化後與移位後的殘差矩陣a的第一行元素一一對應相乘的結果;重複以上步驟n次(權值矩陣b列數),完成反卷積結果矩陣c第一行元素的計算,計算過程如圖4所示;
s1.4順移至殘差矩陣a的第二行元素,計算過程類似步驟1.3,循環n+n次完成反卷積結果矩陣c第二行元素的計算,計算過程如圖5所示;
s1.5順移至殘差矩陣a的第n-1行元素,計算過程類似步驟1.3,循環(n-1)*(n-1)次完成反卷積結果矩陣c第n-1行元素的計算。
s2:反卷積矩陣c中間第n行至m行元素的計算;
由於第n行至m行的計算是由殘差矩陣a所有行元素都參與運算,因此反卷積結果矩陣c的第n行至第m行的每一行元素的計算都要在步驟s1.5的基礎上順移至殘差矩陣a的第n行,計算過程類似步驟s1.3,循環n*n次完成反卷積結果矩陣c中間某一行行元素的計算。
s3:反卷積結果矩陣c後n-1行元素的計算;
s3.1由於步驟s2是由權值矩陣b所有元素參與運算,而步驟s3中是由權值矩陣b的部分行元素參與運算,因此後n-1行元素的計算類似步驟s1,只是和步驟s1中的循環次數有所不同;
s3.2倒數第n-1行元素由權值矩陣b的前n-1行元素參與計算,計算過程類似步驟s1.5;
s3.3倒數第2行元素由權值矩陣b的前2行元素參與計算,計算過程類似步驟s1.4;
s3.4倒數第1行元素由權值矩陣b的前1行元素參與計算,計算過程類似步驟s1.3。
結合圖3,本發明在一個具體應用實例中,詳細流程為:
s100:設卷積神經網絡反向傳播計算中殘差矩陣a的規模為8×8,權值矩陣b的規模為5×5,則反卷積結果矩陣c的規模為12×12,即(8+5-1),一般地,殘差矩陣a放置在向量存儲體,權值矩陣b放置在標量存儲體。
s200:首先計算反卷積結果矩陣c的第1行元素,計算過程如下;
s2.1b4,4×a0,0…b4,4×a0,7b4,4×0b4,4×0b4,4×0b4,4×0;
s2.2b4,3×0b4,3×a0,0…b4,3×a0,7b4,3×0b4,3×0b4,3×0;
s2.3b4,2×0b4,2×0b4,2×a0,0…b4,2×a0,7b4,2×0b4,2×0;
s2.4b4,1×0b4,1×0b4,1×0b4,1×a0,0…b4,1×a0,7b4,1×0;
s2.5b4,0×0b4,0×0b4,0×0b4,0×0b4,0×a0,0…b4,0×a0,7;
s2.6將步驟2.1至步驟2.5每行的12個乘法結果對應相加,累加4次完成反卷積結果矩陣c第1行元素的計算,即2.7,計算過程如圖4所示;
s2.7得出c矩陣第1行元素c0,0c0,1c0,2c0,3c0,4c0,5c0,6c0,7c0,8c0,9c0,10c0,11;
s300:計算反卷積結果矩陣c的第2行元素,由於本次計算涉及到權值矩陣b兩行元素的計算,因此,計算過程比步驟s200多5次循環,計算過程如下;
s3.1b4,4×a1,0…b4,4×a1,7b4,4×0b4,4×0b4,4×0b4,4×0;
s3.2b4,3×0b4,3×a1,0…b4,3×a1,7b4,3×0b4,3×0b4,3×0;
s3.3b4,2×0b4,2×0b4,2×a1,0…b4,2×a1,7b4,2×0b4,2×0;
s3.4b4,1×0b4,1×0b4,1×0b4,1×a1,0…b4,1×a1,7b4,1×0;
s3.5b4,0×0b4,0×0b4,0×0b4,0×0b4,0×a1,0…b4,0×a1,7;
s3.6b3,4×a0,0…b3,4×a0,7b3,4×0b3,4×0b3,4×0b3,4×0;
s3.7b3,3×0b3,3×a0,0…b3,3×a0,7b3,3×0b3,3×0b3,3×0;
s3.8b3,2×0b3,2×0b3,2×a0,0…b3,2×a0,7b3,2×0b3,2×0;
s3.9b3,1×0b3,1×0b3,1×0b3,1×a0,0…b3,1×a0,7b3,1×0;
s3.10b3,0×0b3,0×0b3,0×0b3,0×0b3,0×a0,0…b3,0×a0,7;
s3.11將步驟s3.1至步驟s3.10每行的12個乘法結果對應相加,累加9次完成反卷積結果矩陣c第2行元素的計算,即3.12,計算過程如圖5所示;
s3.12得出c矩陣第2行元素;
c1,0c1,1c1,2c1,3c1,4c1,5c1,6c1,7c1,8c1,9c1,10c1,11;
s400:計算反卷積結果矩陣c的第3行元素,由於本次計算涉及到權值矩陣b三行元素的計算,因此,計算過程比步驟s300多5次循環,計算過程類似步驟s200;
s4.1最終得出c矩陣第3行元素:
c2,0c2,1c2,2c2,3c2,4c2,5c2,6c2,7c2,8c2,9c2,10c2,11;
s500:計算反卷積結果矩陣c的第4行元素,由於本次計算涉及到權值矩陣b四行元素的計算,因此,計算過程比步驟s400多5次循環,計算過程似步驟s200;
s5.1得出c矩陣第4行元素:
c30c31c32c33c34c35c36c37c38c39c310c311;
s600:計算反卷積結果矩陣c的第五行元素,由於本次計算涉及到權值矩陣b五行元素的計算,因此,計算過程比步驟s500多5次循環,計算過程似步驟s200;
s6.1得出c矩陣第5行元素:
c4,0c4,1c4,2c4,3c4,4c4,5c4,6c4,7c4,8c4,9c4,10c4,11;
s700:計算反卷積結果矩陣c的第5—8行元素,由於中間行計算涉及到權值矩陣b五行元素的計算,因此,計算過程如步驟s600;最終計算出反卷積結果矩陣c的第5—8行元素;
s7.1得出c矩陣第5至8行元素:
s800:計算反卷積結果矩陣c的第9行元素,由於權值矩陣b只有前4行參與計算,因此該行計算過程類似步驟s500;
s8.1得出c矩陣第9行元素:
c8,0c8,1c8,2c8,3c8,4c8,5c8,6c8,7c8,8c8,9c8,10c8,11;
s900:計算反卷積結果矩陣c的第10行元素,由於權值矩陣b只有前3行參與計算,因此該行計算過程類似步驟s400;
s9.1得出c矩陣第10行元素:
c9,0c9,1c9,2c9,3c9,4c9,5c9,6c9,7c9,8c9,9c9,10c9,11;
s1000:計算反卷積結果矩陣c的第11行元素,由於權值矩陣b只有前2行參與計算,因此該行計算過程類似步驟s300;
s10.1得出c矩陣第11行元素:
c10,0c10,1c10,2c10,3c10,4c10,5c10,6c10,7c10,8c10,9c10,10c10,11;
s1100:計算反卷積結果矩陣c的第12行元素,由於權值矩陣b只有第1行參與計算,因此該行計算過程類似步驟s200;
s11.1得出c矩陣第12行元素:
c11,0c11,1c11,2c11,3c11,4c11,5c11,6c11,7c11,8c11,9c11,10c11,11。
以上僅是本發明的優選實施方式,本發明的保護範圍並不僅局限於上述實施例,凡屬於本發明思路下的技術方案均屬於本發明的保護範圍。應當指出,對於本技術領域的普通技術人員來說,在不脫離本發明原理前提下的若干改進和潤飾,應視為本發明的保護範圍。
