基於工作模態分析的銑削過程阻尼標定方法與流程
2023-08-01 21:48:06 2
本發明涉及一種銑削過程阻尼標定方法,特別涉及一種基於工作模態分析的銑削過程阻尼標定方法。
背景技術:
切削過程中振動的能量被兩種形式的阻尼吸收,一種是由工件、刀具-刀柄和工具機系統產生的結構阻尼,另一種是由刀具後刀面與工件之間擠壓與摩擦作用而產生的過程阻尼。在穩定性葉瓣圖繪製過程中,如果只考慮結構阻尼而忽略過程阻尼的影響,其穩定性預測結果在較低轉速範圍內與實驗觀測值偏差很大。因此,對過程阻尼的識別具有重要理論及工程應用價值。
文獻「l.tunc,e.budak,identificationandmodelingofprocessdampinginmilling,transactionsofasmejournalofmanufacturingscienceandengineering135(2013)021001.」公開了一種適用於銑削過程阻尼的標定方法。該方法首先利用顫振實驗,通過在轉速固定的情況下逐漸增大切深來獲取穩定性極限切深值;然後根據穩定性求解的逆過程,從獲得的極限切深中反推出過程阻尼係數。但這種方法只適用於穩定切削狀態與不穩定切削狀態界限清晰可辨的情況。
上述文獻的典型特點是:在銑削過程阻尼的識別過程中,如果在穩定性極限切深附近不能清楚判定該切削狀態是穩定切削還是非穩定切削,那麼阻尼識別精度就會有所降低。
技術實現要素:
為了克服現有銑削過程阻尼標定方法實用性差的不足,本發明提供一種基於工作模態分析的銑削過程阻尼標定方法。該方法首先通過標準力錘衝擊實驗獲得刀具-工具機系統模態參數;然後進行無顫振-穩定銑削實驗,利用位移傳感器測量出銑刀刀杆x、y方向上、下兩個位置處的振動信號;求出每個頻率點下所測振動信號的功率譜密度矩陣,將該矩陣進行奇異值分解,然後剔除周期性切削力所對應的特徵值,篩選出主導模態附近、mac值接近1、隨機力激勵所對應的較大特徵值進行傅立葉逆變換,對逆變換結果的峰值和谷值應用指數衰減法來提取平均阻尼係數。得到平均阻尼係數之後,為表徵瞬態下的過程阻尼,先利用切削力和刀尖頻響得到刀尖位置振動幅值,再將其連同平均過程阻尼係數一起帶入x、y兩個方向上建立的能量平衡關係式中,同時求得徑向和切向的犁切力係數;此時,利用所標定出的犁切力係數來表示瞬態下動態犁切力,該動態犁切力即為過程阻尼產生的本質原因。本發明方法能適用於絕對穩定切削與絕對不穩定切削之間界限不明確的情況,通過少量穩定銑削實驗即可標定出過程阻尼係數,實用性好。
本發明解決其技術問題所採用的技術方案:一種基於工作模態分析的銑削過程阻尼標定方法,其特點是包括以下步驟:
步驟一、將加速度計貼在刀尖、刀杆下端和刀杆上端處,力錘在刀尖處進行敲擊,從獲得的頻率響應曲線中提取x和y方向的主導模態參數mx,ζsr,x,ωn,x,和my,ζsr,y,ωn,y,其中mx和my是刀尖處的模態質量,ζsr,x和ζsr,y是刀尖處的結構阻尼比,ωn,x和ωn,y是主導模態頻率,和是刀杆下端和刀杆上端處的模態振型向量。
步驟二、進行無顫振-穩定銑削實驗,利用位移傳感器測量銑刀刀杆x、y方向上刀杆下端和刀杆上端處的振動信號x(t)和y(t),其中x(t)是x方向上刀杆下端和刀杆上端處振動信號時域值組成的向量,y(t)是y方向上刀杆下端和刀杆上端處振動信號時域值組成的向量。
步驟三、將時域中表示的振動信號x(t)進行快速傅立葉變換得到x(jω),x(jω)是刀尖到奈奎斯特頻率之間各個頻率點x方向上刀杆下端和刀杆上端處的振動信號頻域值組成的向量。
步驟四、通過下式計算振動信號的功率譜密度矩陣:
sxx(jω)=x(jω)·xh(jω)
式中,sxx(jω)是x方向上刀杆下端和刀杆上端處振動信號的功率譜密度矩陣,h表示對矩陣進行復共軛轉置操作。
步驟五、對矩陣sxx(jω)進行奇異值分解得到特徵值σx1,σx2和特徵向量ux1,uy1,其中σx1是奇異值分解後得到的較大的特徵值,σx2是奇異值分解後得到的較小的特徵值,ux1是奇異值分解後σx1對應的特徵向量,ux2是奇異值分解後σx2對應的特徵向量。
步驟六、通過下式計算向量和ux1之間的mac值:
式中,mac表示特徵值ux1與模態振型之間的相似程度。
步驟七、在主導模態附近選擇mac值接近1、隨機激勵力所對應的σx1進行傅立葉逆變換,剔除周期性切削力所對應的σx1。
步驟八、對步驟七中傅立葉逆變換結果峰值與谷值的絕對值取對數運算後,進行線性擬合,得到擬合直線的斜率s,s表示擬合所得到直線的斜率。
步驟九、通過下式計算x方向上產生的總阻尼比:
式中,ζx是x方向上的總阻尼比。
步驟十、通過下式計算x方向上產生的平均過程阻尼係數:
cpr,x=2mxωn,x(ζx-ζsr,x)
式中,cpr,x是x方向上的平均過程阻尼係數。
步驟十一、重複步驟三至步驟十,計算y方向上產生的平均過程阻尼係數cpr,y,cpr,y是y方向上的平均過程阻尼係數。
步驟十二、利用切削力和刀尖位置頻響得到銑削過程中刀尖位置振動幅值x0,y0和振動頻率f0,其中x0是x方向振動幅值,y0是y方向振動幅值,f0是振動頻率。
步驟十三、通過下式計算x、y方向上刀尖位置振動速度:
式中,是x方向振動速度,是y方向振動速度。
步驟十四、通過下式計算動態犁切體積:
式中,vdy,ij是銑刀第i個刀齒上第j個單元參與切削時的動態犁切體積,v是切削線速度,lw是刀尖磨損帶長度,θij是銑刀第i個刀齒上第j個單元參與切削時的切觸角,zij是銑刀第i個刀齒上第j個單元的軸向高度。
步驟十五、通過聯立下式求解切向和徑向犁切力係數:
式中,kp,t是切向犁切力係數,kp,r是徑向犁切力係數,t是主軸旋轉周期,n是銑刀齒數,nel是銑刀軸向單元的數目。
本發明的有益效果是:該方法首先通過標準力錘衝擊實驗獲得刀具-工具機系統模態參數;然後進行無顫振-穩定銑削實驗,利用位移傳感器測量出銑刀刀杆x、y方向上、下兩個位置處的振動信號;求出每個頻率點下所測振動信號的功率譜密度矩陣,將該矩陣進行奇異值分解,然後剔除周期性切削力所對應的特徵值,篩選出主導模態附近、mac值接近1、隨機力激勵所對應的較大特徵值進行傅立葉逆變換,對逆變換結果的峰值和谷值應用指數衰減法來提取平均阻尼係數。得到平均阻尼係數之後,為表徵瞬態下的過程阻尼,先利用切削力和刀尖頻響得到刀尖位置振動幅值,再將其連同平均過程阻尼係數一起帶入x、y兩個方向上建立的能量平衡關係式中,同時求得徑向和切向的犁切力係數;此時,利用所標定出的犁切力係數來表示瞬態下動態犁切力,該動態犁切力即為過程阻尼產生的本質原因。本發明方法能適用於絕對穩定切削與絕對不穩定切削之間界限不明確的情況,通過少量穩定銑削實驗即可標定出過程阻尼係數,實用性好。
下面結合附圖和具體實施方式對本發明作詳細說明。
附圖說明
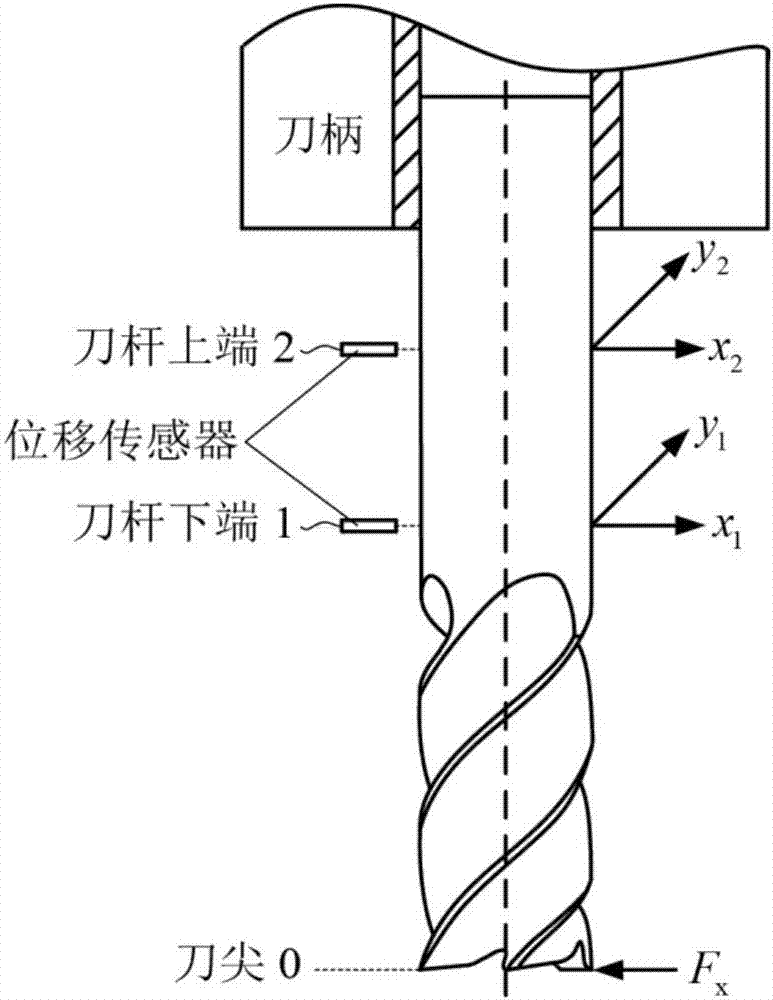
圖1是本發明基於工作模態分析的銑削過程阻尼標定方法所涉及銑刀的示意圖。
圖2是本發明方法實施例x方向特徵值σx1。
圖3是本發明方法實施例x方向特徵值σx1傅立葉逆變換結果。
圖4是本發明方法實施例y方向特徵值σy1。
圖5是本發明方法實施例y方向特徵值σy1傅立葉逆變換結果。
圖6是本發明實施例預測穩定性葉瓣圖與實測顫振數據的對比圖。
具體實施方式
參照圖1-6。本發明基於工作模態分析的銑削過程阻尼標定方法具體步驟如下:
步驟一、實驗選定半徑為6mm、螺旋角為35°、法向前角為10°,后角為5°,刀尖圓弧半徑20μm,齒數為4的硬質合金立銑刀在三坐標立式加工中心對鋁合金7050-t7451進行順銑切削。將加速度計貼在刀尖0、刀杆下端1和刀杆上端2處,力錘在刀尖0處進行敲擊,從獲得的頻率響應曲線中提取x和y方向的主導模態參數mx=0.3193kg,ζsr,x=1.79%,ωn,x=1060hz,和my=0.3971kg,ζsr,y=2.35%,ωn,y=1041hz,其中mx和my是刀尖0處的模態質量,ζsr,x和ζsr,y是刀尖0處的結構阻尼比,ωn,x和ωn,y是主導模態頻率,和是刀杆下端1和刀杆上端2處的模態振型向量。
步驟二、進行無顫振-穩定銑削實驗,利用位移傳感器測量銑刀刀杆x、y方向上刀杆下端1和刀杆上端2處的振動信號x(t)和y(t),其中x(t)是x方向上刀杆下端1和刀杆上端2處振動信號時域值組成的向量,y(t)是y方向上刀杆下端1和刀杆上端2處振動信號時域值組成的向量。
步驟三、將時域中表示的振動信號x(t)進行快速傅立葉變換得到x(jω),x(jω)是0到奈奎斯特頻率之間各個頻率點x方向上刀杆下端1和刀杆上端2處的振動信號頻域值組成的向量。
步驟四、通過下式計算振動信號的功率譜密度矩陣:
sxx(jω)=x(jω)·xh(jω)
式中,sxx(jω)是x方向上刀杆下端1和刀杆上端2處振動信號的功率譜密度矩陣,h表示對矩陣進行復共軛轉置操作。
步驟五、對矩陣sxx(jω)進行奇異值分解得到特徵值σx1,σx2和特徵向量ux1,uy1,其中σx1是奇異值分解後得到的較大的特徵值,σx2是奇異值分解後得到的較小的特徵值,ux1是奇異值分解後σx1對應的特徵向量,ux2是奇異值分解後σx2對應的特徵向量。
步驟六、通過下式計算向量和ux1之間的mac值:
式中,mac表示特徵值ux1與模態振型之間的相似程度。
步驟七、在主導模態附近選擇mac值接近1、隨機激勵力所對應的σx1進行傅立葉逆變換,剔除周期性切削力所對應的σx1。
步驟八、對步驟七中傅立葉逆變換結果峰值與谷值的絕對值取對數運算後,進行線性擬合,得到擬合直線的斜率s=-0.2279,s表示擬合所得到直線的斜率。
步驟九、通過下式計算x方向上產生的總阻尼比:
式中,ζx是x方向上的總阻尼比。
步驟十、通過下式計算x方向上產生的平均過程阻尼係數:
cpr,x=2mxωn,x(ζx-ζsr,x)
=2×0.3193×2×π×1060×(7.24%-1.79%)
=231.8n/(m/s)
式中,cpr,x是x方向上的平均過程阻尼係數。
步驟十一、重複步驟三至步驟十,計算y方向上產生的平均過程阻尼係數cpr,y=407.8n/(m/s),cpr,y是y方向上的平均過程阻尼係數。
步驟十二、利用切削力和刀尖位置頻響得到銑削過程中刀尖位置振動幅值x0=49μm,y0=64μm和振動頻率f0=46.67hz,其中x0是x方向振動幅值,y0是y方向振動幅值,f0是振動頻率。
步驟十三、通過下式計算x、y方向上刀尖位置振動速度:
式中,是x方向振動速度,是y方向振動速度。
步驟十四、通過下式計算動態犁切體積:
式中,vdy,ij是銑刀第i個刀齒上第j個單元參與切削時的動態犁切體積,v是切削線速度,lw是刀尖磨損帶長度,θij是銑刀第i個刀齒上第j個單元參與切削時的切觸角,zij是銑刀第i個刀齒上第j個單元的軸向高度。
步驟十五、通過聯立下式求解切向和徑向犁切力係數:
經聯立求解得kp,r=40059n/mm3,kp,t=14386n/mm3,式中kp,t是切向犁切力係數,kp,r是徑向犁切力係數,t是主軸旋轉周期,n是銑刀齒數,nel是銑刀軸向單元的數目。
通過圖6可以看出,採用實施例中所標定犁切力係數繪製的穩定性葉瓣圖在較低的轉速範圍內能很好的與實測顫振結果相匹配,證明了本發明標定方法的準確性。
