一種測量數據丟失情況下的多目標跟蹤方法與流程

2023-04-25 06:49:41

本發明涉及目標跟蹤技術領域，特別是一種測量數據丟失情況下的多目標跟蹤方法。

背景技術：

隨著非傳統防務及安全挑戰的不斷湧現，多目標跟蹤算法的研究成為一個熱點。而在多目標跟蹤算法中，有兩類主要方法，數據關聯(如PDA、JPDA)和繞過關聯直接處理(如PHD、CPHD)。在目標個數較多且含雜波時，數據關聯(PDA等)的計算量會非常大，不利於工程應用。而近年來，多目標跟蹤研究專家Ronald P.S.Mahler教授提出了基於有限集統計學(FISST)的隨機有限集(random finite set，RFS)理論，在此基礎上推出概率假設密度(Probability Hypothesis Density，PHD)濾波器。PHD濾波方法將集函數積分方法變換為單個目標的積分，它首先跟蹤整個目標群，隨後再去檢測每個變量，然而PHD濾波也存在一些問題，如漏檢敏感，無數目分布等。針對這一問題，Ronald P.S.Mahler教授提出了勢概率假設密度(CPHD)濾波器，相比較PHD濾波器，CPHD濾波器能在傳遞概率密度假設函數的基礎上對目標的數目分布也進行更新，在目標的估計方面做的比PHD更好。

在實際雷達量測信息中，由於大多數採用機載脈衝都卜勒雷達，而都卜勒盲區不可避免的會存在並導致部分目標測量信息的丟失，從而影響濾波精度。因此，需要一個魯棒的濾波算法，能夠在目標量測數據丟失(雷達盲區)情況下保持其濾波精度。在濾波過程中，改進算法更新中的增益矩陣是一種常見的方法，通過引入比例因子調節濾波算法的增益矩陣，降低算法在目標數據丟失時給濾波精度帶來的影響，以提高濾波器的魯棒性。雖然CPHD濾波器的性能優於PHD濾波器，但是CPHD濾波器的計算量也比PHD濾波器多得多，在CPHD濾波器中，計算複雜度為O(NM3)，而相比之下在PHD濾波器中的計算複雜度只有O(NM)，其中N為跟蹤的目標數目，M為當前觀測集中的觀測數目。從計算複雜度可以看出，CPHD濾波器比PHD濾波器大，而當前觀測集中的觀測數目M作為計算複雜度的關鍵部分也比跟蹤的目標數目N要大。目前，高斯混合概率假設密度濾波器(GM-CPHD)進行目標跟蹤時，在雷達都卜勒存在盲區，且計算複雜度過大、計算效率低。

技術實現要素：

本發明的目的在於提供一種測量數據丟失情況下的多目標跟蹤方法，通過引入比例因子提高濾波器的魯棒性，通過自適應門限減小計算量。

實現本發明目的的技術解決方案為：一種測量數據丟失情況下的多目標跟蹤方法，包括以下步驟：

步驟1，對於多目標跟蹤，目標狀態集Xk＝{xk,1,…,xk,m(k)}，m(k)是目標狀態向量個數，下標k表示k時刻；目標狀態隨機有限集Ξk＝Sk(Xk-1)∪Nk(Xk-1)，其中Sk(Xk-1)、Nk(Xk-1)分別為原保存和新產生的目標隨機有限集；k時刻新生目標強度函數其中分別代表第i個新生目標的權值、均值和協方差矩陣，Jγ,k為新生目標的總數；真實目標和雜波源的新生概率假設密度為勢分布為

步驟2，初始化初始目標的概率假設密度D0(x)及勢分布p0(n)；

步驟3，預測：對目標狀態集Xk在k+1時刻的概率假設密度及勢分布進行預測，k≥1，得到k+1時刻的概率假設密度Dk+1|k(x)及勢分布pk+1|k(n)；

步驟4，更新：對目標狀態集Xk在k+1時刻的概率假設密度及勢分布進行更新，k≥1，得到此時刻的概率假設密度及勢分布Dk+1(x)、pk+1(n)；

步驟5，修剪合併：對目標集強度函數υk+1(x)的高斯項進行修剪合併，提取目標狀態估計進行性能評估；

步驟6，重複步驟3～5，對目標進行跟蹤直至目標消失。

本發明與現有技術相比，其顯著優點為：(1)在傳遞PHD函數的同時傳遞目標數分布，並對概率假設密度及勢分布進行預測和更新，可以在雜波環境下對目標的狀態和數目準確的估計；(2)比例因子的引入，可以通過調節算法的增益矩陣提高濾波器的魯棒性，解決雷達都卜勒盲區的數據丟失問題；(3)自適應門限的設定，對減小濾波器的計算量起到良好的作用，使GM-CPHD濾波器的工程應用成為可能。

附圖說明

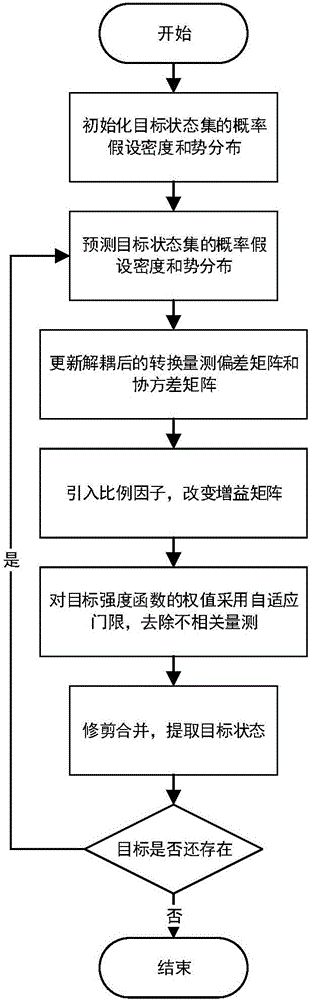
圖1是本發明測量數據丟失情況下的多目標跟蹤方法的流程圖。

圖2是機載雷達與目標相對位置示意圖。

圖3是目標量測信息圖。

圖4是本發明濾波結果圖。

圖5是本發明與傳統方法估計的目標個數圖。

圖6是OSPA距離圖。

圖7是三個算法OSPA距離比較差值圖。

圖8是各目標都卜勒頻率變化圖。

圖9是算法運行耗費時間對比圖。

具體實施方式

下面結合附圖及具體實施例對本發明做進一步詳細說明。

結合圖1，本發明測量數據丟失情況下的多目標跟蹤方法，具體步驟如下：

步驟1，對於多目標跟蹤，它的目標狀態集Xk＝{xk,1,…,xk,m(k)}，m(k)是目標狀態向量個數，下標k表示k時刻；目標狀態隨機有限集Ξk＝Sk(Xk-1)∪Nk(Xk-1)，其中Sk(Xk-1)、Nk(Xk-1)分別為原保存和新產生的目標隨機有限集；k時刻新生目標強度函數其中分別代表第i個新生目標的權值、均值和協方差矩陣，Jγ,k為新生目標的總數；真實目標和雜波源的新生概率假設密度為勢分布為

步驟2，初始化：主要包括初始目標的概率假設密度D0(x)及勢分布p0(n)，具體如下：

初始目標的概率假設密度D0(x)及勢分布p0(n)的關係為：

D0(x)＝n0·s0(x)

其中，s0(x)為概率密度，s0(x)峰值對應先驗的目標位置；初始目標的勢分布p0(n)是目標數n的概率分布，p0(n)期望值為n0，即：

在高斯勢概率假設密度方法中，初始概率假設密度D0(x)符合高斯分布，D0(x)由每個目標的正態分布概率和表示；而初始勢分布選擇為二項分布，則：

其中，[0,L]為目標滿足均勻分布的區間，n0為初始目標數的推測值，n0＝Lq0，q0為二項式分布發生概率，為伯努利分布、CL,n為分布係數。

步驟3，預測：對目標狀態集Xk在k+1時刻的概率假設密度及勢分布進行預測，k≥1，得到k+1時刻的概率假設密度Dk+1|k(x)及勢分布pk+1|k(n)，具體如下：

在勢概率假設密度濾波器中：目標運動是獨立的、不相關的，即目標x在k時刻雷達中出現的概率為bk(x)是確定的，與目標個數、狀態等無關，同理目標消失的概率也一樣。

在k時刻，已知的參數有：概率假設密度Dk(x)、目標數的期望nk、勢分布Pk(x)，k時刻存活下來的目標狀態集Xk的概率假設密度如下：

Dk+1|k(ξ)＝∫ps(x')·fk+1|k(x|x')·Dk|k(x')dx'

其中：ps(x')表示目標存活概率，取0.9；fk+1|k(x|x')表示單目標馬兒可夫轉移密度；Dk|k(x')表示前一時刻目標狀態集Xk的概率假設密度，則k時刻目標狀態集Xk的概率假設密度Dk+1|k(x)＝b(x)+∫ps(x')·fk+1|k(x|x')·Dk|k(x')dx'，b(x)為衍生目標概率；

勢分布：

其中：pk+1|k(n)為k+1時刻的預測值、j為樣本數、ps為目標存活概率、Jk為k個高斯成分、為k時刻期望目標數，代表第j個目標的權值，Nmax代表勢分布的最大可能數，pk(l)代表前一時刻即k時刻的目標存活概率，代表二項式係數；

目標數的期望值預測：

其中：分別代表期望的新生目標數和存活目標數。

步驟4，更新：對目標狀態集Xk在k+1時刻的概率假設密度及勢分布進行更新，k≥1，得到此時刻的概率假設密度及勢分布Dk+1(x)、pk+1(n)。包括對真實協方差矩陣和真實偏差進行無偏轉換並解耦合；分析都卜勒頻移背景下的傳感器測量數據丟失現象，引入比例因子調節系統增益矩陣；設置自適應門限對量測集合進行簡化，減小當前觀測集中的觀測數目M，具體如下：

在預測目標狀態的強度函數和預測目標狀態集的勢分布pk+1|k已知，且高斯混合的情況下，可以得到CPHD濾波器的更新方程如下：

勢分布更新：

目標狀態的強度函數更新：

目標數更新：

其中

其中，δj(·)為均衡函數，κk(·)為雜波強度函數。

4.1)盲區內的跟蹤算法

在實際雷達量測信息中，由於大多數採用機載脈衝都卜勒雷達，而都卜勒盲區不可避免的會存在並導致部分目標測量信息的丟失，從而影響濾波精度。因此，需要一個魯棒的濾波算法，能夠在目標量測數據丟失(雷達盲區)情況下保持其濾波精度。在濾波過程中，改進算法更新中的增益矩陣是一種常見的方法，通過引入比例因子調節濾波算法的增益矩陣，降低算法在目標數據丟失時給濾波精度帶來的影響，以提高濾波器的魯棒性。

在三維坐標系中，目標運動時的都卜勒頻移可以表示為：

其中Vt和Va分別是目標和載機的運動速度，φ是載機航線與雷達間的偏角，β是目標與載機間的航向偏角。

機載雷達上靜止目標的都卜勒頻移為：

都卜勒盲區為|fdt|≤Δf，其中fdt＝fd-fdc。此時的都卜勒盲區就為[-Δf,Δf]，目標都卜勒頻移為：

其中，vr是目標相對於傳感器的徑向速度，f0是目標輻射源的發射頻率，c是目標輻射源信號的傳播速度，分別是目標速度矢量在x，y，z方向上的分量，分別是載機速度矢量在x，y，z方向上的分量。

基於此，本發明提出了一種魯棒的UCM-CPHD濾波算法，具體如下：

首先，定義量測誤差向量為e(k+1)：

其中，y(k+1)是第k+1時刻的目標笛卡爾坐標系下的量測值，是第k+1時刻的預測值，它們是3×1的向量。

然後，在增益矩陣求取公式中添加一個n維方陣S(k)用來調節GM-CPHD濾波器的增益矩陣，可得：

E(k+1)＝H(k+1)P(k+1|k)HT(k+1)+(S(k)-I)R0(k+1)+R(k+1)

其中，I是單位陣，H為觀測矩陣，R0(k+1)是對角陣，其對角元素的取值為平均真實偏差R(k+1)的對角元素，即在MATLAB中計算公式如下：

R0(k+1)＝diag(diag(R(k+1)))

且E(k+1)計算公式如下：

ξ是滑動窗口數目，也就是求取E(k+1)所需數據的數量。

由此可得S(k)的計算公式:

設增益調節矩陣為S*(k)，它是用來調節增益矩陣，求取公式如下：

Sii(k)是S(k)的i行i列元素，即S(k)對角線上的第i個元素。

整理後，改進的R-UCM-CPHD濾波算法迭代步驟如下：

步驟一：求取去偏轉換量測卡爾曼濾波狀態初值和估計協方差矩陣初值P(0)。設需要濾波的目標狀態變量包含目標在笛卡爾坐標系上的位置、速度和加速度，因為是三維的，故包含三個坐標軸方向的位置和速度共九個變量，組成9×1向量。將接收到的前兩組目標測量值代入公式，求得前三組數據的量測噪聲協方差矩陣：R(1)、R(2)和R(3)，並根據下式求取卡爾曼濾波初值和P(0|0)：

其中

設當接收到第二組量測數據時，目標狀態變量的真實值為X，則狀態量測誤差為：

則估計協方差矩陣的初值P(0|0)為：

步驟二：計算目標狀態預測值

步驟三：計算預測估計值協方差矩陣

P(k+1|k)＝F(k)P(k|k)FT(k)+Γ(k)Q(k)ΓT(k)

步驟四：求出解耦後的量測轉換的均值偏差u(k+1)，協方差R(k+1)和無偏量測值Z(k+1)，特別的，當目標數據丟失時，將使用預測值來代替量測值。

真實協方差矩陣和真實偏差中添加偏差補償因子，進行無偏估計並解耦合，得到改進的和代入更新方程，求取真實協方差矩陣和真實偏差公式如下：

μ＝E[υm|rm,θm]＝[μx,μy,μz]T

分別是和的協方差，μx、μy、μz分別為偏差μ在x、y、z軸上的投影，為協方差矩陣中的量。

噪聲協方差矩陣是一個3×3的對稱矩陣，其中非對角線上的元素Rxy,Ryz,Rxz代表著x,y,z軸的噪聲耦合相，在協方差矩陣R中，相對於主對角線上的元素Rxx,Ryy,Rzz，非對角線上的元素的影響可以忽略，此時的協方差矩陣R可以簡化成對角矩陣，即Rnew＝diag(Rxx,Ryy,Rzz)，則解耦後的協方差矩陣Rnew的計算量是未解耦前的33/(3×13)＝9倍。具體解耦細節如下：

在笛卡爾坐標繫上，噪聲協方差矩陣R可以描述為；

Rnew＝MRMT

其中，M是轉移矩陣。

此時，轉換後的噪聲協方差矩陣Rnew可以寫成：

Rnew＝diag(Rxx,Ryy,Rzz)

步驟五：求出增益調節矩陣S*(k)

步驟六：計算增益矩陣

K(k+1)＝P(k+1|k)HT(k+1)[H(k+1)P(k+1|k)HT(k+1)+(S*(k)-I)R0(k+1)+R(k+1)]-1

步驟七：計算濾波估計值.

步驟八：計算濾波估計值協方差矩陣.

P(k+1|k+1)＝P(k+1|k)-K(k+1)H(k+1)P(k+1|k)

步驟九：返回步驟二，並使k+1後進行迭代。

與傳統的UCM-CPHD算法不同的是，R-UCM-CPHD算法主要是對計算增益矩陣的公式進行修改，加入了增益調節矩陣S*(k)，當預測數據與量測數據誤差很大時，此時很可能產生了奇異值甚至數據丟失。此時增益調節矩陣S*(k)通過之前的目標數據信息，對增益矩陣進行調節，減小盲區導致的數據丟失對濾波估計值和協方差的影響。這樣，R-UCM-CPHD算法能夠改進傳統的UCM-CPHD算法在盲區導致的數據丟失時的濾波性能，具有很好的魯棒性。

4.2)自適應門限

在CPHD濾波器中，算法的計算量主要來自每個更新周期都要計算M+1個元素的均衡函數(即前文提到的δj(·))，其計算複雜度為O(NM3)，而相比之下在PHD濾波器中的計算複雜度只有O(NM)，由此可知，減小M值能更有效的降低計算複雜度。

設γ為跟蹤門限的大小，觀測維數M，殘差協方差矩陣S(k)，則殘差向量d(k)的範數為g(k)＝dT(k)S-1(k)d(k)，g(k)為服從自由度為M的分布，當g(k)≤γ時，跟蹤門規則滿足。

首先計算出目標量測數據落入跟蹤門內的概率PG，結合跟蹤門規則可得：其中跟蹤門的體積為其中係數由觀測空間的維數nz決定(c1＝2，c2＝π，c3＝4π/3)。

設置自適應門限去掉所有和已知被探測目標不相關的量測數據，設γ為自適應跟蹤門限的大小，觀測維數M，殘差協方差矩陣S(k)，此時門限γ滿足(nz＝3)：

其中，PD為檢測概率，β為新源密度；根據公式，門限γ與殘差協方差矩陣S(k)有關，而S(k)是一個與目標狀態集有關的變量。從公式中可以看出，門限γ與殘差協方差矩陣S有關，而S是一個與目標狀態集有關的變量。

門限所包含的區域落入聯合門限區域的量測集合就可以表示為：與傳統算法相比，採用自適應門限可能會去掉所有和已知被探測目標不相關的量測數據，減小計算量。

最後更新目標狀態的強度函數υk+1|k(x)及勢分布pk+1|k(n)，由於量測集合由Zk變化為引起雜波強度函數變化為則更新公式

雜波強度的變化直接影響到勢概率假設密度濾波器中高斯分量對應權值和量測狀態集的變化，而後者的大小M恰恰是CPHD濾波器計算複雜度O(NM3)的關鍵部分，所以通過自適應門限可以有效的減小濾波器的計算量。

步驟5，修剪合併：對目標集強度函數υk+1(x)的高斯項進行修剪合併，提取目標狀態估計進行性能評估。首先修剪，該步驟需要將小於權值τ的高斯成分濾掉。

式中是大於閾值的權值，為單個高斯分量的權值，為GM-CPHD函數中單個高斯分量的均值，為目標狀態協方差矩陣，x為目標狀態集，為與目標狀態、均值和協方差矩陣有關的函數，為k+1時刻的概率假設密度函數；

然後合併，當一些高斯成分間的距離小於閾值U時，需要將這些高斯成分合併；最後提取權值大於τ1的高斯成分。

最後狀態估計，目標的狀態估計是提取權值大於τ1的高斯成分，其提取公式如下：其中，為單個高斯分量的權值，為GM-CPHD函數中單個高斯分量的均值，τ1為設定的門限。

性能評價：對於多目標跟蹤算法的性能評價指標，一般採用均方誤差(MSE)、均方根誤差(RMSE)、圓丟失概率(CPEP)、Wasserstein距離和OSPA距離等。一般OSPA距離可以通過水平參數c來很好地體現多目標跟蹤算法對位置和目標數目跟蹤的性能。OSPA距離定義如下：

其中，

步驟6，重複步驟3～5，對目標進行跟蹤直至目標消失。

實施例1

本發明的效果可以通過以下仿真實驗進一步說明：

1.仿真條件

假設目標狀態其中位置單位是m，速度單位是m/s。本仿真有四個目標，各個目標運動模型是CA模型，且四個目標的初始狀態如下：

Xt1＝[300m,300m,40m,-20m/s,-20m/s,-1m/s,0m/s2,0m/s2,-2m/s2]T；

Xt2＝[40m,-300m,-300m,1m/s,20m/s,20m/s,2m/s2,0m/s2,0m/s2]T；

Xt3＝[200m,300m,300m,-1m/s,-20m/s,-20m/s,-2m/s2,0m/s2,0m/s2]T；

Xt4＝[-200m,40m,-200m,20m/s,-1m/s,20m/s,0m/s2,-2m/s2,0m/s2]T；

目標的運動方程：

仿真實驗假設目標1的出生時刻為第0s，死亡時刻為第7s，目標2的出生時刻為第7s，死亡時刻為25s，目標3的出生時刻為第11s，死亡時刻為37s，目標4的出生時刻為25s，死亡時刻為第40s。設雷達採樣周期T＝1s，徑向距離量測方差方位角與高低角量測方差取檢測概率PD＝0.99，目標存活概率PS＝0.9，合併閾值U＝4，裁剪閾值τ＝1e-5，狀態估計閾值τ1＝0.5，最大高斯數Jmax＝100。

新出現的目標符合泊松過程,bk(x)＝N(x,mb,Pb),

mb＝[300m,300m,40m,-20m/s,-20m/s,-1m/s,0m/s2,0m/s2,-2m/s2]T,

Pb＝diag(104×[5,5,5,1,1,1,0.5,0.5,0.5]),Q＝diag(10-2×[1,1,1])。

2.仿真內容和結果分析

生成的目標量測信息如圖3所示，量測信息中含有目標信息和雜波信息。

各算法目標位置估計與去除雜波後的量測值和真實值對比如圖4所示。圖中CPHD代表正常情況下的UCM-AG-CPHD，CPHD2代表加盲區情況下的UCM-AG-CPHD，CPHD3代表改進後的加盲區R-UCM-AG-CPHD。從圖中可以看出，各CPHD算法可以對多個目標同時跟蹤。

算法各個時刻估計的目標個數結果如圖5所示，可以看出，各算法的估計精度大於90％，且盲區對目標數目估計的影響較小。

由OSPA距離結果圖6可以看出，各CPHD算法不管是對目標數目的估計，還是對目標位置的估計都具有很好地性能。

三個算法OSPA距離比較如圖7，從圖中可以看出，R-UCM-AG-CPHD算法在多目標跟蹤方面有著良好的性能，改進的算法(CPHD3)的跟蹤精度優於不改進的算法(CPHD2)，說明改進方法具有良好的效果，但顯然會比沒有盲區的算法(CPHD1)精度低。藍色部分代表CPHD3-2，即改進的盲區算法與未改進的盲區算法的OSPA距離差，在16～18s目標1發生機動，數據丟失；在26～28s目標2數據丟失；在31～33s目標3數據丟失；在36～38s目標4數據丟失。對應圖中可以看到相應的時間內改進的算法OSPA距離小於未改進的(即藍色線條＜0)，仿真表明，改進的算法對目標機動產生的盲區有良好的效果。

目標都卜勒頻率(徑向速度)隨仿真次數的變化情況如圖8所示。根據公式可知，目標都卜勒盲區區間是[-100 100]HZ，其中各目標運動軌跡有一段落入都卜勒盲區內，分別是在16～18s目標1；在26～28s目標2；在31～33s目標3；在36～38s目標4數據丟失。在這段區域內，雷達的目標數據將會受到嚴重影響。

通過多次實驗，得到本發明改進的算法和傳統UCM-PHD算法耗費時間如圖9中，從可知在保證算法性能的前提下，本算法比改進前的計算量相比降低8.6％左右，新算法在計算效率上的優勢十分明顯，具有更好的工程應用前景。