用於滾動軸承智能故障診斷的方法與流程
2023-05-23 02:05:46 1
本發明涉及一種滾動軸承故障診斷方法,核心是基於小波包變換和奇異值分解的滾動軸承故障特徵提取技術以及基於PNN神經網絡的模式識別技術。
背景技術:
滾動軸承是旋轉機械的關鍵零部件之一,在使用過程中受到機械應力、磨損等一系列物理作用,使軸承發生形變、腐蝕等損傷。同時,由於加工製造工藝的不規範以及裝配不當等原因,軸承也會產生人為損傷,這些損傷的累積與加深最終導致了軸承的故障。一旦軸承發生故障,將導致機組停機,甚至發生重大生產事故。因此,滾動軸承的故障診斷至關重要。
當前滾動軸承的故障診斷大多採用振動分析法作為技術手段,在故障特徵提取方面主要是通過時域、頻域以及時頻分析三種方法。然而,時域和頻域方法只能從整體上描述振動信號的特徵,割裂了信號時域和頻域的聯繫,不能詳細的反映振動信號的內在信息。在滾動軸承故障診斷的研究中,故障的徵兆和故障類型存在很複雜的非線性數學關係,使得診斷的合適的數學模型很難找到。時頻分析方法能夠在時域和頻域上反映信號的特徵。小波變換是目前信號時頻分析中常用的方法之一,但是它只能夠對低頻段信號進行分解,對於信號的高頻部分不再進行處理,而滾動軸承的故障特徵信息往往集中在信號的中高頻段,這就限制了小波變換在滾動軸承故障診斷中的應用。從小波變換發展而來的小波包分解技術不僅體現信號低頻段的近似部分,也能體現信號高頻段的細節部分,因而在處理非線性及非平穩信號的領域中具有非常明顯的優勢。
故障診斷的關鍵在於故障特徵的提取,矩陣奇異值是矩陣的固有特徵,通過對矩陣的奇異值分解可以有效提取矩陣中的關鍵信息。奇異值具有良好的穩定性,即當矩陣元素發生小的變動時,矩陣的奇異值變化也很小,這個性質可以有效地降低測量噪聲對振動信號特徵提取的影響;同時,矩陣的奇異值可以通過少數的值表徵原矩陣的特性,從而降低特徵矩陣的維數,有利於提高神經網絡的診斷精度和速度。
概率神經網絡(PNN)是一種用於模式分類的神經網絡。概率神經網絡是基於統計原理的神經網絡模型,在分類功能上與最優貝葉斯分類等價,其實質是基於貝葉斯最小風險準則發展而來的一種並行算法,同時它不像傳統的多層前向網絡那樣需要BP算法進行反向誤差傳播的計算,而是完全前向的計算過程。它訓練時間短、不易產生局部最優,而且它的分類正確率較高。
技術實現要素:
本發明的目的在於提供一種用於滾動軸承智能故障診斷的方法,該方法易於實現、精度高、實時性好,適用於滾動軸承故障診斷。
實現本發明目的的技術解決方案為:
一種用於滾動軸承智能故障診斷的方法,包括以下步驟:
1)利用加速度傳感器獲取滾動軸承振動信號;
2)採用小波包變換對滾動軸承振動信號進行分解並重構;
3)運用奇異值分解方法對重構信號進行奇異值分解,將各頻段的奇異值組合成特徵向量;
4)將滾動軸承不同狀態下的特徵向量構成特徵矩陣,並輸入到PNN神經網絡中進行訓練,得到訓練好的PNN神經網絡;
5)將振動信號經步驟2)、3)特徵提取後輸入到訓練好的PNN神經網絡中進行故障模式識別。
本發明與現有技術相比,其顯著優點為:(1)本發明首先採用小波包變換的方法對軸承振動信號進行分解和重構,能夠將振動信號分解到不同頻段,以較高的時頻解析度凸顯各頻段重構信號中所蘊含的軸承故障信息;(2)對重構後的不同頻段信號進行奇異值分解,提取出軸承的故障特徵向量,能夠有效地降低測量噪聲對振動信號特徵提取的影響,同時降低特徵矩陣的維數,並且該特徵向量具有良好的聚類性和可分性,有利於提高神經網絡的診斷精度和速度;(3)採用PNN神經網絡,能夠自動的對滾動軸承的故障進行識別,不需要人工觀察頻譜特性,自動化程度和可靠性較高,並可依據計算機網絡實現滾動軸承的遠程故障診斷和狀態監測。
附圖說明
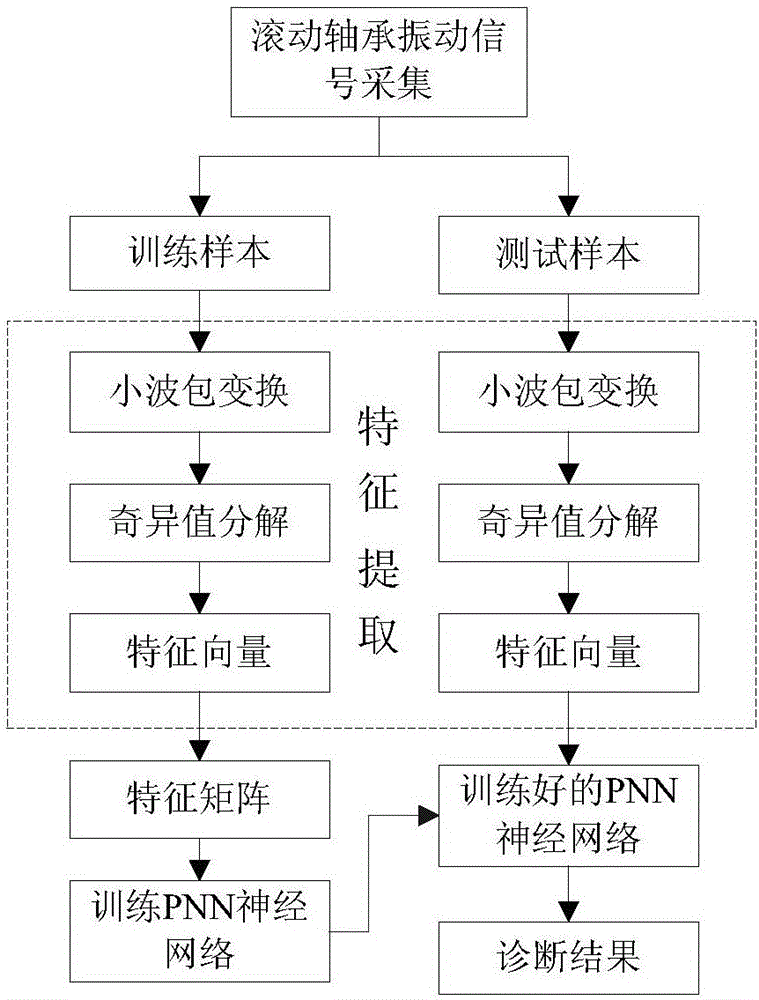
圖1為本發明用於滾動軸承智能故障診斷的方法流程圖。
圖2為滾動軸承正常狀態振動信號。
圖3為滾動軸承內圈故障振動信號。
圖4為滾動軸承外圈故障振動信號。
圖5為滾動軸承滾動體故障振動信號。
圖6為滾動軸承振動信號的三層小波包分解樹示意圖。
圖7為滾動軸承正常狀態下8個頻段的重構信號。
圖8為滾動軸承不同狀態下的振動信號特徵向量柱狀圖。
圖9為滾動軸承振動信號特徵向量的三維效果圖。
圖10為概率神經網絡拓撲結構示意圖。
圖11為採用PNN神經網絡的分類結果。
具體實施方式
下面結合附圖和實施例,對本發明的具體實施方式作進一步詳細闡述。
本發明所述的一種用於滾動軸承智能故障診斷的方法,流程圖如圖1所示,包括以下步驟:
1)利用加速度傳感器分別採集滾動軸承在正常、內圈故障、外圈故障以及滾動體故障四種狀態下的振動信號,如圖2~5所示。
2)採用小波包變換對振動信號進行分解並重構,得到各頻段的重構信號。其具體包括以下步驟:
2.1)對振動信號X進行零均值化處理。X=X-E(X),式中,E(·)是求均值。
2.2)對零均值化後的振動信號進行小波包分解。利用MATLAB中小波包分解函數wpdec,其調用格式為Tr=wpdec(X,L,'wname'),L為小波包分解層數,wname為小波基函數。本實施例中設置L=3,wname=db3,採用db3小波基函數對滾動軸承振動信號進行3層小波包分解,其中Tr為小波包分解樹,包含了8個頻段的小波包係數,如圖6所示為滾動軸承振動信號的3層小波包分解樹示意圖。
2.3)對8個頻段的小波包係數進行重構。利用MATLAB中的小波包係數重構函數wprcoef,該函數的調用格式為S3,i=wprcoef(Tr,[3,i]),其中S3,i(i=0,1,2,…7)即為8個重構信號,[3,i]表示第3層第i個節點。滾動軸承正常狀態下8個頻段的重構信號如圖7所示。
3)運用奇異值分解技術對重構信號進行奇異值分解,將各頻段的奇異值組合成為滾動軸承特徵向量。其具體包括以下步驟:
3.1)分別計算8個重構信號的奇異值,奇異值是矩陣具有的固有特徵,能夠充分反映矩陣中元素包含的內在信息。
其中:Ui∈Rm×m為正交矩陣,Vi∈Rn×n為正交矩陣,Σi∈Rm×n為對角矩陣,其中Σi對角線上的非零元素λi為重構信號S3,i的奇異值,則該分解稱為S3,i的奇異值分解。
3.2)將各頻段的奇異值組合成滾動軸承特徵向量p,作為PNN神經網絡的輸入。
p=[λ0,λ1,λ2,λ3,λ4,λ5,λ6,λ7]
隨機選取滾動軸承不同狀態下的一組振動信號,其特徵向量如表1所示。
表1滾動軸承振動信號特徵向量
附圖8.為滾動軸承不同狀態下的振動信號特徵向量柱狀圖,從圖中可以看出,滾動軸承不同狀態下的特徵向量有著很明顯的差別。附圖9.為滾動軸承振動信號特徵向量的三維效果圖。從圖中可以看出,利用小波包變換與奇異值分解提取出的滾動軸承特徵向量具有良好的聚類性以及可分性。說明小波包與奇異值分解能夠有效地表徵軸承故障特徵。
4)將滾動軸承不同狀態下的特徵向量構成特徵矩陣,並輸入到PNN神經網絡中進行訓練,得到訓練好的PNN神經網絡。具體包括以下步驟:
4.1)設置滾動軸承故障四種工作狀態的類別向量,如表2所示。
表2滾動軸承故障類別向量
PNN神經網絡的輸入為滾動軸承四種狀態下振動信號經特徵提取後的特徵向量;輸出為代表滾動軸承四種工作狀態的類別向量,(1,0,0,0)對應正常狀態,(0,1,0,0)對應滾動體故障,(0,0,1,0)對應內圈故障,(0,0,0,1)對應外圈故障。
4.2)利用MATLAB中的newpnn函數構建PNN神經網絡,該函數的調用格式為net=newpnn(P,T,spread);其中net為訓練好的PNN神經網絡,P為輸入矩陣,T為目標矩陣,spread為擴展速度;附圖6.為PNN神經網絡的結構示意圖。PNN神經網絡輸入層有8個神經元,分別對應特徵向量p中的8個特徵值;輸出層有4個神經元,分別對應類別向量的四個元素值。
4.3)將滾動軸承四種工作狀態的特徵向量構成輸入矩陣P,將相應的類別向量構成目標矩陣T,spread值為14,選取訓練集對PNN神經網絡進行訓練,保存訓練好的神經網絡作為識別網絡。
5)將振動信號經特徵提取後輸入到訓練好的PNN神經網絡中進行故障模式識別。
圖11為採用PNN神經網絡的分類結果,從圖中可以看出,訓練好的PNN神經網絡能準確識別出軸承的工作狀態。
