一種基於自適應遺傳算法的立體車庫優化方法與流程
2023-05-13 01:36:12 1
本發明涉及立體車庫優化方法,尤其是一種立體停車庫杆件結構優化方法。
背景技術:
當前城市居民私人車輛急劇增長不僅使得城市道路交通擁堵,而且造成城區停車日益艱難。發展立體式停車場可以有效地緩解城市交通難問題,因為立體車庫比較普通平面式停車場有如下好處:1)車輛停車向空間發展,從而節省平面停車場過多佔用城市寶貴用地面積;2)可以十分有效地解決城市居住人口密集區停車難的困境。設計經久耐用的立體車庫停車設施是重要的,由於立體車庫鋼結構骨架起著支承停放車輛載荷和分擔提升機構載荷的作用,因此車庫鋼結構骨架進行合理的結構分析和設計對於車庫整體承載穩定性起著決定性作用。
技術實現要素:
為了克服已有立體車庫的承載穩定性較差的不足,本發明提供一種承載穩定性較好的基於自適應遺傳算法的立體車庫優化方法。
本發明解決其技術問題所採用的技術方案是:
一種基於自適應遺傳算法的立體車庫優化方法,包括以下步驟:
1)通過原有設計參量建立立體車庫承載有限元模型,計算出每個杆件承載最大彎矩載荷以及最大承載變形數值;
2)構造立體車庫鋼結構骨架優化設計總重量目標函數,並對所需的設計參量進行當量化;
3)為保證車庫結構骨架具有足夠的強度、剛度以及穩定性,設定結構應力和節點位移不大於許用值作為約束條件,採用自適應遺傳算法,得到立體車庫優化方案。
進一步,所述步驟2)中,對部件中的非圓形截面的梁杆部件可以當量成圓形部件來處理,因此當量圓形杆件總重量作為目標函數W, 其其中,f(d)為當量圓形杆件總重量,ρ為材料密度,di為當量圓形杆件直徑,Li當量圓形杆件長度,m需要優化的杆件數量。
再進一步,所述步驟3)中,作為優化目標總重量函數的前提條件:承載杆件的最大應力以及最大撓度不大於對應的許用值為約束條件,構造最優化設計的數學模型:
其中,Mmax為最大彎矩,ymax為最大中性軸距離,E為材料的彈性模量AC為直梁杆件長度,考慮結構應力耦合效應;CD為橫梁承載杆件長度,[y]為最大撓度,[σ]為許用應力。
更進一步,所述步驟3)中,所述自適應遺傳算法中,交叉概率和變異概率進行改進:
其中,fmax—群體中量大的適應度,favg—每代群體的平均適應度,f′—要交叉的兩個個體中較大的適應度;f—要變異個體的適應度值,交叉概率pc,變異概率pm,pc1,pc2分別為交叉概率的最大值和最小值,pm1,pm2分別為變異概率的最大值和最小值,A為自適應遺傳算法模型係數;
通過對pc和pm進行調整,對於適應度值高於群體平均適應度值的個體,pc和pm取較小值,使得該解得以保護進入下一代,而低於平均適應度值的個體,pc和pm取較大值,使得該解被淘汰掉。
所述步驟3)中,所述自適應遺傳算法的處理過程如下:
3.1)開始
GA=(MN,f,c,m,pc,pm),迭代條件為,迭代次數達到MAX次,MN為群體大小,f為個體適應度評價函數,這裡為目標函數,c為交叉操作算子,m為變異操作算子,pc為交叉概率,pm為變異概率;
進入遺傳算法的遺傳優化,依次進行選擇、交叉、變異三種遺傳方式,並不斷循環這個過程直到達到終止條件;
3.2)編碼方法
採用二進位編碼方法,對待優化的結構設計優化變量進行編碼;
3.3)產生初始種群
優化對象di的取值範圍為[ai,bi],利用隨機的方法,產生MN個個體的種群,個體t的優化變量為[d1,d2,...,dM,dM+1,dM+2,...,dM+N];
3.4)個體評價
個體評價函數為修正後的目標函數;
3.5)性能是否滿足
判斷迭代次數是否滿足迭代次數條件;
3.6)最優保存選擇操作
按目標函數的值從小到大排序,選取所有種群中MN個個體進行最優保存;
3.7)變異操作和交叉操作。
本發明的技術構思為:立體停車庫鋼結構承載框架(見附圖1)由底部、中部和頂部結構架組成。底部作為車輛進出車庫和車輛調頭之用,高度最大。中部為標準層,用來停放車輛,它由標準單元組成,可以根據實際車庫容量來適當加減層數。頂部用來安裝滑輪組並留有檢修滑輪組及其他設備的空間,高度最小。鋼結構分段製造,用高強度螺栓在現場拼裝。
立體車庫結構優化設計數學模型:停車庫鋼結構骨架結構由眾多構件組成,為簡化計算和減小構件尺寸規格,停車庫鋼結構可分為梁單元M組,杆單元N組,同一組單元截面積相等。優化設計變量為構件面積,並按型鋼規格取離散值。設計變量為X=[x1,x2,...,xM,xM+1,xM+2,...,xM+N]T,式中x1,x2,...,xM為第1~M組梁單元的截面積,xM+1,xM+2,...,xM+N為第1~N組杆單元的截面積直徑。停車庫鋼結構骨架的總重量為優化設計的目標函數為
式中ρi、Ai(xi)、Li第i個單元的密度,截面積和長度,M+N是單元總數。
對部件中的非圓形截面的梁當量成圓形杆件,截面積為目標函數為
式中di為當量直徑
約束條件:為保證停車庫鋼結構骨架具有足夠的強度、剛度和穩定性,以結構應力和節點位移不大於許用值作為減輕結構總重量設計的約束條件, 即
式中σmax(di),Umax(di)表示為結構中的最大應力和最大節點位移。為許用節點應力和許用節點位移。
約束條件為:
a)彎曲強度:最大彎矩約為Mmax,通過建立承載有限元模型計算出,彎曲強度校核公式為ymax為求應力的點離中性軸的最大距離。Iz則是橫截面對於中性軸z的慣性矩,式中
彎曲強度所決定的約束條件為:
b)根據剛度要求,最大撓度[y]≤4.0mm,即材料的拉伸壓縮彈性模量E。
剛度所決定的約束條件為:
構造最優化設計的數學模型:採用罰函數法來處理不等式約束問題,即計算出由於違背約束條件而產生的罰函數c,並用它修正目標函數。具體的做法:若不滿足上述不等式,即gj(di)>0,cj=gj(di);反之若滿足上式,cj=0。於是罰函數匯總為
修正後的目標函數為
f(di)=F(di)(1+kc) (4)
其中係數k是一常數,它的取值應視約束條件的重要性而定。
本發明的有益效果主要表現在:承載穩定性較好。
附圖說明
圖1是立體車庫鋼結構示意圖,其中,(a)是正視圖,(b)是側視圖。
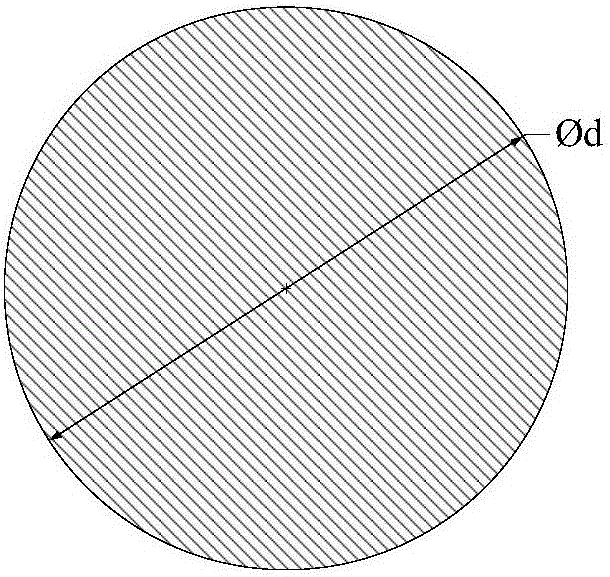
圖2是杆件當量直徑示意圖。
圖3是自適應遺傳算法的流程圖。
圖4是現有遺傳算法和改進遺傳算法計算結果比較圖。
具體實施方式
下面結合附圖對本發明作進一步描述。
參照圖1~圖4,一種基於自適應遺傳算法的立體車庫優化方法,包括以下步驟:
1)通過原有設計參量建立立體車庫承載有限元模型,計算出每個杆件承載最大彎矩載荷以及最大承載變形數值;
2)構造立體車庫鋼結構骨架優化設計總重量目標函數,並對所需的設計參量進行當量化;
3)為保證車庫結構骨架具有足夠的強度、剛度以及穩定性,設定結構應力和節點位移不大於許用值作為約束條件,採用自適應遺傳算法,得到立體車庫優化方案。
進一步,所述步驟2)中,對部件中的非圓形截面的梁杆部件可以當量成圓形部件來處理,因此當量圓形杆件總重量作為目標函數W, 其中,f(d)為當量圓形杆件總重量,ρ為材料密度,di為當量圓形杆件直徑,Li當量圓形杆件長度,m需要優化的杆件數量。
再進一步,所述步驟3)中,作為優化目標總重量函數的前提條件:承載杆件的最大應力以及最大撓度不大於對應的許用值為約束條件,構造最優化設計的 數學模型:
其中,Mmax為最大彎矩,ymax為最大中性軸距離,E為材料的彈性模量AC為直梁杆件長度,考慮結構應力耦合效應;CD為橫梁承載杆件長度,[y]為最大撓度,[σ]為許用應力。
更進一步,所述步驟3)中,所述自適應遺傳算法中,交叉概率和變異概率進行改進:
其中,fmax—群體中量大的適應度,favg—每代群體的平均適應度,f′—要交叉的兩個個體中較大的適應度;f—要變異個體的適應度值,交叉概率pc,變異概率pm,pc1,pc2分別為交叉概率的最大值和最小值,pm1,pm2分別為變異概率的最大值和最小值,A為自適應遺傳算法模型係數;
通過對pc和pm進行調整,對於適應度值高於群體平均適應度值的個體,pc和pm取較小值,使得該解得以保護進入下一代,而低於平均適應度值的個體,pc和 pm取較大值,使得該解被淘汰掉。
所述步驟3)中,所述自適應遺傳算法的處理過程如下:
3.1)開始
GA=(MN,f,c,m,pc,pm),迭代條件為,迭代次數達到MAX次,MN為群體大小,f為個體適應度評價函數,這裡為目標函數,c為交叉操作算子,m為變異操作算子,pc為交叉概率,pm為變異概率;
進入遺傳算法的遺傳優化,依次進行選擇、交叉、變異三種遺傳方式,並不斷循環這個過程直到達到終止條件;
3.2)編碼方法
採用二進位編碼方法,對待優化的結構設計優化變量進行編碼;
3.3)產生初始種群
優化對象di的取值範圍為[ai,bi],利用隨機的方法,產生MN個個體的種群,個體t的優化變量為[d1,d2,...,dM,dM+1,dM+2,...,dM+N];
3.4)個體評價
個體評價函數為修正後的目標函數;
3.5)性能是否滿足
判斷迭代次數是否滿足迭代次數條件;
3.6)最優保存選擇操作
按目標函數的值從小到大排序,選取所有種群中MN個個體進行最優保存;
3.7)變異操作和交叉操作。
實例:結構分為7組單元為例說明,梁單元M=5組,杆單元N=2組,待優化的參量為[d1,d2,...,d7]。所選用鋼材料密度ρ=7850kg/m3。應力強度小於等於100MPa以及許用撓度小於等於4mm。運用MATLAB遺傳算法工具箱進行求解, 種群規模為30,進化代數為100,初始交叉率Pc1=0.6,Pc2=0.3;初始變異率Pm1=0.05,Pm2=0.001。
設定立體車庫模型基本參數:底部為2.6m;中部為2.2m;頂部高度為1.5m。車庫設計容量為20輛,需要10層停車標準單元,這樣車庫總層數為12層,總高度為H=2.6+10×2.2+1.5=26.1m。採用三維梁單元和杆單元模擬實際結構建立有限元模型,用固定約束邊界條件模擬結構在基礎上的安裝情況。梁單元具有拉伸、壓縮、扭轉和彎曲能力,每個節點有6個自由度,截面形狀儘量選取市場上有售的型材。杆單元為單向拉壓單元,每個節點有3個移動自由度。整個車庫鋼結構骨架共有330個單元,172個節點。除考慮停車庫鋼結構骨架自重和機械傳動系統的重量外,還考慮每個車位均受額定車輛載荷的作用情況。這裡的停車庫共有20個車位,額定車輛載荷為1600kg。鋼結構骨架的受力情況主要包括:鋼結構本身自重,結構架上各停車位的車輛及固定叉梳重量,提升系統制動所產生的慣性力,驅動裝置的重力,頂部梁架所受滑輪組和配重的重力,整體結構所受的風力、地震載荷以及由於外界環境溫度變化而引起的溫度應力等,它們以集中或均布方式作用。按基本載荷作用情況,將停車庫鋼結構骨架結構分析的計算工況分為。如表1所示的4種工況:
表1
結果分析以及結論:優化設計與原設計方案結果比較見表2。表中d1~d7分別為角柱、前後側中間立柱、左右橫柱、前後橫柱、上下支承柱、左右腹杆、前後腹杆的當量直徑。從表1可以看出,傳統自適應遺傳算法得到的優化設計方案較原方案有很大改進,可使結構重量降低30%左右。經過改進的自適應遺傳算法可以使結構重量降低41%。由此可見,採用新的自適應遺傳算法建立鋼結構骨架優化設計模型,對鋼結構骨架進行優化設計,可進一步降低材料的消耗,從而提高車庫製造成本的經濟性。
表2
交叉概率和變異概率進行改進的思路:遺傳算法的參數中交叉概率pc和變異概率pm的選擇是影響遺傳算法行為和性能的關鍵所在,直接影響算法的收斂性,pc越大,新個體產生的速度就越快。然而過大時遺傳模式被破壞的可能性也越大,使得具有高適應度的個體結構很快就會被破壞;但是如果pc過小,就不易產生新的個體結構;如果pm過小,就不易產生新的個體結構;如果pm取值過大,那麼遺傳算法就變成了純粹的隨機搜索算法。針對不同的優化問題,需要反覆實驗來確定pc和pm,本專利針對立體車庫結構採用一種自適應遺傳算子,使pc和pm能夠隨適應度自動改變。當種群各個體適應度趨於一致或者趨於局部最優時,使pc和pm增加,而當群體適應度比較分散時,使pc和pm減少。同時對於適應值高於群體平均適應值的個體,對應於較低的pc和pm,使該解得以保護進入下一代,而低於平均適應值的個體,結合個體違反約束的情況給予相對較高的pc和pm,使該解得以保護進入下一代;而低於平均適應值的個體,結合個體違反約束的情 況給予相對較高的pc和pm,使該解得以保護進入下一代;而低於平均適應值的個體,結合個體違反約束的情況給予相對較高的pc和pm,使該解被淘汰掉。因此,自適應的pc和pm能夠提供相對某個解的最佳pc和pm。通過自適應遺傳算子使算法在保持群體多樣性的同時,保證遺傳算法的收斂性。通過對最優保護遺傳算法中的pc和pm按照上述思想進行改進,使得算法中的pc和pm按如下公式進行自適應調整,得到傳統自適應算法:
式中fmax—群體中量大的適應度;favg—每代群體的平均適應度;f′—要交叉的兩個個體中較大的適應度;f—要變異個體的適應度值。當適應度值低於平均適應度值時,說明該個體是性能不好的個體,對它就採用較大的交叉率和變異率;如果適應度值高於平均適應度值,說明該個體性能優良,對它就根據其適應度值取相應的交叉率和變異率。可以看出,當適應度值越接近最大適應度時,交叉率和變異率就越小;當等於最大適應度值時,交叉率和變異率的值為零。這種調整方法對於群體處於後期比較合適,但對於進化初期不利,因為進化初期群體中的個體幾乎處於一種不發生變化的狀態,而此時的優良個體不一定是優化的全局最優解,這容易使進化走向局部最優解得可能性增加。為此,可以進一步的改進,使群體中最大適應度值的個體的交叉率和變異率不為零,分別提高到pc2和pm2這就相應地提高了群體中表現優良的個體的交叉率和變異率,使得它們不會處於一種近似停滯不前的狀態。為了保證每一代的優良個體不被破壞,採用最優保護策略,使它們複製到下一代中。經過上述改進,pc和pm計算表達式如下:
pc=pc1(1+kc) f'<farg (7)
pm=pm1(1+kc) f<farg
式中:pc1,pc2分別為交叉概率的最大值和最小值,pm1,pm2分別為變異概率的最大值和最小值。這個算法採用精英策略起著保護和推廣個體的作用,但是當個體數目過大的時,會使較差的個體變異能力下降,導致種群進化陷入停滯不前,造成局部收斂。容易產生局部最優解。為了克服以上兩種遺傳算法的不足,本專利自適應遺傳算法的交叉概率和變異概率進行改進:
這樣,通過對pc和pm進行調整,對於適應度值高於群體平均適應度值的個體,pc和pm取較小值,使得該解得以保護進入下一代,而低於平均適應度值的個體,pc和pm取較大值,使得該解被淘汰掉。故這種方法可提供某個解相對較佳的pc和pm,在保持群體多樣性的同時,保證GA的多樣性。
