一種球形貯箱微重力環境下液體晃動的建模方法與流程
2023-05-04 23:33:26 1
本發明應用於充液太空飛行器液體晃動分析領域,具體來說是一種球形貯箱微重力環境下液體晃動的建模方法。
背景技術:
根據太空飛行器飛行過程中所受過載的情況,貯箱中流體的運動可分為失重、微重、低重、常重和超重數種工況,對於自旋充液太空飛行器,還有快旋和慢旋工況等。對於充液太空飛行器,主要研究失重或微重以及低重工況和自旋工況的流體運動特性。理論和實踐表明,當bond數(其中ρ是液體的密度;g為過載加速度;l0為特徵長度,一般取為自由液面的半徑;σ為表面張力係數)為0時,可視為失重工況;當bond數介於0到100之間時,可視為微重工況,當bond數大於100時,可視為低重工況甚至常重工況研究其運動特性的影響,這時可忽略表面張力的影響。
貯箱晃動液體晃動問題的研究方法可分為理論研究、數值研究、實驗研究等三類。在理論研究方面,20世紀60年代,abramson首先應用不可壓縮、無粘、無旋的線性勢流理論建模,將流體動力學方程演繹為速度勢的拉普拉斯方程,具有線性化的邊界條件,採用分離變量法可以得到了速度勢特徵函數和特徵頻率的解析解。實際上,只有少數幾種形狀的容器,可使用分離變形量法對上述拉普拉斯方程的邊值問題進行解析求解。對於一般形狀容器,由於壁面幾何結構的複雜性,很難直接用解析方法求解,需要進一步結合數值方法進行分析求解。數值研究的方法依據所採用的理論模型的不同,主要可分為兩類:一類是基於勢流理論得到時空分離的動力學方程,從而通過特徵值分析實現頻域解耦的研究方法。另一類則直接從navier-stokes方程出發,對液體晃動進行時域的數值仿真,通常稱為cfd(計算流體動力學)方法。無論是理論研究,還是數值研究,它們結果的正確性常需要通過實驗來檢驗。
目前,低重環境下充液貯箱小幅線性晃動的動力學特性研究比較成熟,其理論模型廣泛應用於太空飛行器的工程設計。但隨著太空飛行器的發展,高定位精度太空飛行器貯箱內的液體晃動面臨新問題。太空飛行器具有較高的定位精度,在姿態機動穩定過程中,使得太空飛行器貯箱面臨微重力學環境,貯箱內推進劑的表面張力開始顯現,可能導致貯箱內推進劑的晃動呈現複雜晃動特性,對平臺高精度姿態控制產生影響。目前已有的小幅線性晃動建模方法已然不能滿足其動力學特性預測的需求。
微重環境小幅液體晃動問題目前基本採用基於計算流體力學的商業軟體進行求解,獲得力和力矩的時域曲線,但該方法一方面直接用於控制系統設計較為困難,另一方面求解效率較低,求解耗時較長,難以滿足工程需要。因此,有必要開發一種高效的適用於工程應用的微重小幅液體晃動建模方法。
技術實現要素:
本發明解決的技術問題是:提出一種球形貯箱微重力環境下液體晃動的建模方法,可將微重力環境下球形貯箱內的液體晃動問題等效為三軸彈簧-質量系統的振動問題,可直接用於控制系統中實現控制系統設計。
本發明的技術解決方案是:一種球形貯箱微重力環境下液體晃動的建模方法,包括下列步驟:
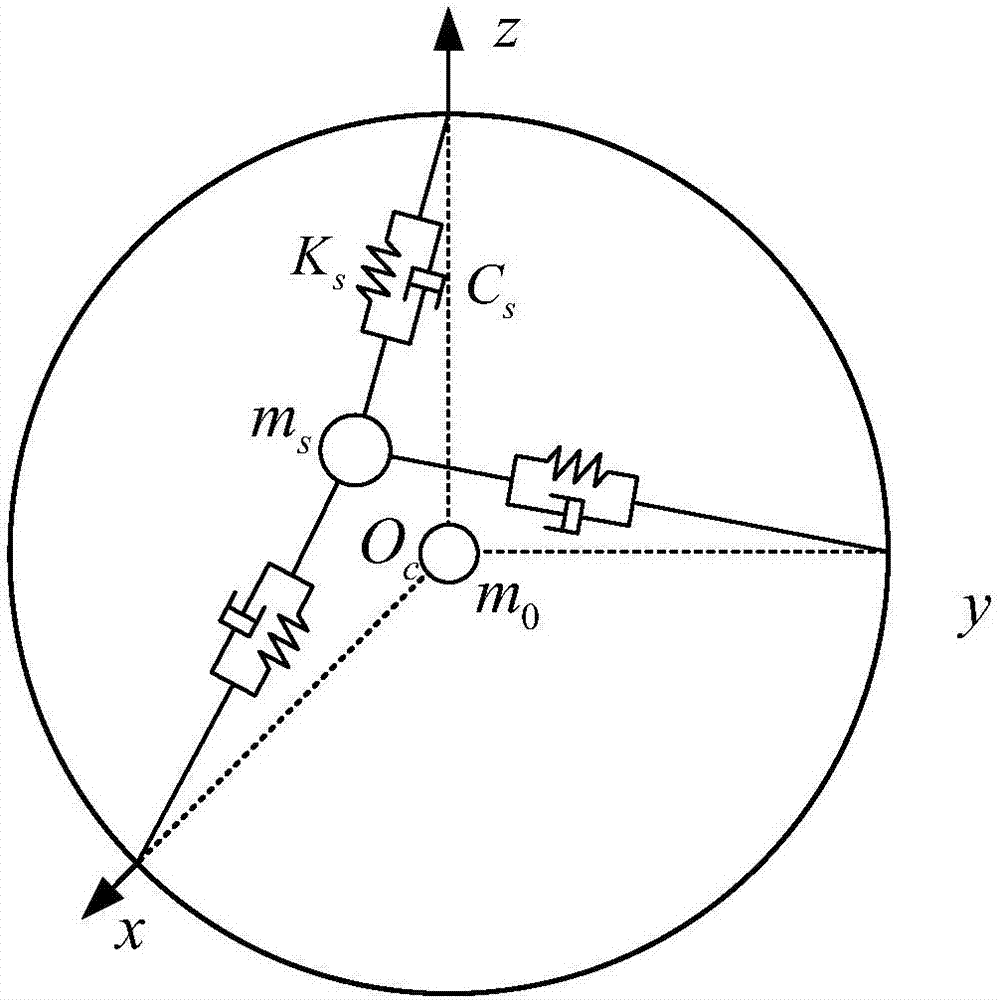
(1)、建立球形貯箱微重力環境下液體晃動的等效力學模型,所述等效力學模型為三軸彈簧-質量等效力學模型,它包含一個靜止質量m0和一個晃動質量ms,其中,靜止質量m0位於球形貯箱中心;晃動質量通過三個剛度係數為ks、阻尼係數為cs的彈簧阻尼器與貯箱連接,晃動質量處於平衡位置時,三個彈簧阻尼器方向分別與球形貯箱三軸重合;
(2)、計算球形貯箱零重力環境下液體晃動的n階固有頻率ω0i和模態φi,所述n≥1;
(3)、假設液體在微重力的作用下發生晃動,基於球形貯箱零重力環境下液體晃動的n階固有頻率ω0i和模態φi,推導貯箱內液體晃動時液體施加於貯箱壁面的作用力和液體相對貯箱晃動的動能,並依據其與步驟(1)中建立的等效力學模型作用力和動能等效原則,計算得到步驟(1)中所建立等效力學模型的晃動質量ms和靜止質量m0。
所述步驟(2)的具體步驟為:
(2.1)、假設球形貯箱液體處於零重力環境下,液體在貯箱內形成一個處於全溼形態,內部有球形空腔的流體域,定義sf為液體自由液面,sw為固體壁面,sf和sw之間為流體域,球心至sf之間為空腔,球心至自由液面的距離為rm,f為自由液面發生波動時的波高;
(2.2)、建立(2.1)中所述流體域的流體動力學方程,獲得流體域處於零重力環境下的自由液面sf上的動力學邊界條件、自由液面上的運動學邊界條件和貯箱壁面處的邊界條件:
流體域處於零重力環境下的自由液面sf上的動力學邊界條件為:
式中,δ為拉普拉斯算子,為流體域的勢函數
自由液面sf上的動力學邊界條件表示為:
式中,ρ是液體密度,σ為表面張力係數;
自由液面上的運動學邊界條件為:
貯箱壁面處的邊界條件為:
(2.3)、假設步驟(2.1)中所述流體域在球形貯箱內的小幅晃動為頻率為ω的振動,將勢函數和波高描述為:
式中,和f』為和f對時間的導數;
(2.4)、以球形空腔半徑rm為特徵長度,引入無量綱量r、f、φ、ω:
(2.5)、將步驟(2.2)中的勢函數和波高f以步驟(2.3)的形式代入,並以步驟(2.4)中的無量綱形式進行整理,獲得流體域無量綱形式的流體動力學方程、流體域在固體壁面處的邊界條件和流體域在自由液面處的邊界條件:
流體域無量綱形式的流體動力學方程:δφ=0
流體域在固體壁面處的邊界條件:
流體域在自由液面處的邊界條件:
(2.6)、將步驟(2.5)中的三個方程寫成galerkin變分形式方程:
式中:sw表示固體壁面,sf代表自由液面,v表示流體域δφ表示對φ取變分;
(2.7)、將步驟(2.6)中的方程前兩項進行高斯變換,並將液體在自由液面處的邊界條件簡化為獲得:
(2.8)、對流體域劃分三維實體網格,在每個單元內有:
式中,代表φ在單元結點j處的值,nj為第j個單元的單元插值函數,ne為單元結點數;
(2.9)、將步驟(2.8)所得到φ代入至步驟(2.7)的公式中,根據變分的任意性推導得到單元剛度陣和單元質量陣:
單元剛度陣:
單元質量陣:
式中,j∈[1,ne],k∈[1,ne];
(2.10)、基於(2.9),結合(2.8)劃分的三維網格,利用有限元分析方法將單元剛度陣和單元質量陣組裝成為整個流體域的液體剛度矩陣和液體質量矩陣,根據整個流體域的液體剛度矩陣和液體質量矩陣,通過特徵值求解方法獲得整個流體域的n階ωi、φi和模態坐標qi,i∈[1,n],所述n≥1;
(2.11)、計算流體域液體晃動的n階固有頻率ω0i和模態φi為:
所述步驟(3)的具體步驟為:
(3.1)、定義參考坐標系o0xyz和obxyz分別為慣性坐標系和貯箱本體坐標系,假設本體坐標系原點ob與球心oc重合,將勢函數描述成:
式中,r為某液體質點相對於ob點的矢徑,rb是ob相對於o0的矢徑,φi和qi分別為第i階液體晃動模態和模態坐標,n為參與計算的模態階數;
(3.2)、計算液體對貯箱的作用力:
(3.2a)、依據步驟(3.1)得到的勢函數形式,計算獲得流場動壓pd為:
為rb相對於時間變量t的二階倒數,為模態坐標qi相對於時間變量t的一階倒數;
(3.2b)、依據流場動壓pd,計算液體對貯箱的作用力:
其中,n為貯箱壁面處的外法向單位矢量,mliq為流體域液體質量;
(3.3)、計算液體相對於貯箱晃動的動能:
(3.3a)、依據步驟(3.1)得到的勢函數定義,獲得流體速度u:
(3.3b)、計算液體相對於貯箱的動能:
(3.4)、計算等效力學模型產生的作用力和動能,採用步驟(2)所述的等效力學模型時,貯箱受到的作用力fe和等效力學模型相對於貯箱運動的動能te分別表示為:
式中,rs為晃動質量ms相對於oc點的矢徑;
(3.5)、將步驟(3.3)和步驟(3.4)中獲得的作用力和動能進行等效,即:f=fe、t=te,得到晃動質量ms和靜止質量m0:
m0=mliq-ms;
(3.6)、根據晃動質量ms、靜止質量m0和流體域液體晃動的第1階固有頻率ω01,確定彈簧阻尼器的剛度係數ks和阻尼係數cs:
ks=msω012
步驟(3.6)中所述液體晃動阻尼比根據貯箱壁面邊界層內和液體內部的平均能量耗散率dw和di得到:
式中,分別代表貯箱壁面邊界層內和液體內部的平均能量耗散率,式中,ν為液體的粘度,u代表貯箱壁面附近的流體速度,r(φ)表示為:
本發明與現有技術相比的有益效果是:
(1)、本發明明確微重環境下貯箱內液體初始時刻為全溼形態,將微小的重力不作為過載處理,而當作外部激勵處理,這樣即可將微重力環境下的液體晃動問題轉化為具有固有力學特性系統的受迫晃動問題,從而為等效力學模型的建立和求解奠定可行性基礎。
(2)、本發明獲得的三軸彈簧-質量等效力學模型,用晃動質量ms、靜止質量m0、彈簧阻尼器的剛度係數ks和阻尼係數cs四個參數描述球形貯箱微重力環境下的液體晃動特性,該模型形式簡單,可直接加入到太空飛行器系統的動力學方程中,獲得包含微重環境液體晃動的整星動力學方程。可應用於太空飛行器的動力學預測以及控制系統的設計;
(3)、本模型中等效力學模型的晃動質量ms、靜止質量m0、彈簧阻尼器的剛度係數ks和阻尼係數cs均通過理論推導獲得,使用簡單,實用性強。
附圖說明
圖1本發明實施例的微重力球形貯箱中的自由液面;
圖2本發明實施例的球形貯箱三軸彈簧-質量等效力學模型示意圖;
圖3本發明實施例的球形貯箱等效系統動力學建模;
圖4本發明實施例的微重環境小幅晃動力對比圖;
圖5本發明實施例的微重環境小幅晃動力矩對比圖。
具體實施方式
以下結合附圖和具體實施例對本發明進行詳細描述。
球形貯箱微重力環境下液體晃動建模的困難在於如何將微重力環境下液體晃動這一流體動力學問題轉化為等效力學振動問題,以描述微重力環境下液體晃動的頻率特徵及貯箱的受力特性。
球形貯箱內部液體處於微重力環境下時,液體在貯箱內處於全溼形態,形成球形的內部空腔,如圖1所示,球形貯箱內部液體在外部激勵的作用下發生小幅晃動。
本發明基於對球形貯箱在微重力環境下晃動特性的認識,提出了一種球形貯箱微重力環境下液體晃動的建模方法。該建模方法說明如下:
(1)、建立球形貯箱微重力環境下液體晃動的等效力學模型。
由於液體發生小幅晃動時,大部分液體仍將包裹在貯箱壁面上跟隨貯箱一起運動,因此這部分液體用靜止質量表示,其位置始終位於貯箱中心。將晃動質量看作質點,其平衡位置也位於貯箱中心,而液體小幅晃動用其相對於平衡位置的振動來描述。等效力學模型為三軸彈簧-質量等效力學模型,它包含一個靜止質量m0和一個晃動質量ms,其中,靜止質量m0位於球形貯箱中心;晃動質量通過三個剛度係數為ks、阻尼係數為cs的彈簧阻尼器與貯箱連接,晃動質量處於平衡位置時,三個彈簧阻尼器方向分別與球形貯箱本體坐標系三軸重合。如圖2所示。
(2)、計算球形貯箱零重力環境下液體晃動的n階固有頻率ω0i和模態φi,所述n≥1。
(2.1)、假設球形貯箱液體處於零重力環境下,液體在貯箱內形成一個處於全溼形態,內部有球形空腔的流體域,定義sf為液體自由液面,sw為固體壁面,sf和sw之間為流體域,球心至sf之間為空腔,球心至自由液面的距離為rm,f為自由液面發生波動時的波高。如圖1所示。
(2.2)、建立(2.1)中所述流體域的流體動力學方程,獲得流體域處於零重力環境下的自由液面sf上的動力學邊界條件、自由液面上的運動學邊界條件和貯箱壁面處的邊界條件。
(a)、建立球坐標系oc-rθα,坐標原點oc位於球心,依據勢流理論,建立流體域的流體動力學方程,即流體域的勢函數的laplace方程:
式中,δ為拉普拉斯算子,(r,θ,α)為流體域質點的球坐標,r為質點到原點的距離,θ為方位角,即質點與原點oc的連線與ocz軸正向的夾角,α為ocx軸按逆時針方向旋轉到質點與原點oc的連線在oxy面上的投影時所轉過的最小正角。
(b)、根據牛頓第二定律,獲得自由液面sf上的動力學邊界條件。
球坐標系下,自由液面上的二倍平均主曲率k表示為:
式中,div是散度算子,grad為梯度符號,也可用符號表示。
在靜平衡狀態下,二倍平均主曲率簡化為km:
當液體發生小幅晃動時,可將k在靜平衡液面附近展開,有:
因此,自由液面sf上的動力學邊界條件表示為:
式中,ρ是液體密度,σ為表面張力係數。
(c)、自由液面上的運動學邊界條件為以速度勢函數形式表徵的速度和波高形式表徵的速度相等,即:
(d)、貯箱壁面處的邊界條件即為貯箱壁面處的不可滲透條件:貯箱壁面處速度為0,即:
(2.3)、假設步驟(2.1)中所述流體域在球形貯箱內的小幅晃動為頻率為ω的振動,將勢函數和波高描述為:
式中,和f』為和f對時間的導數。
(2.4)、以球形空腔半徑rm為特徵長度,引入無量綱量r、f、φ、ω:
(2.5)、將步驟(2.2)中的勢函數和波高f以步驟(2.3)的形式代入,並以步驟(2.4)中的無量綱形式進行整理,可獲得流體域無量綱形式的流體動力學方程、流體域在固體壁面處的邊界條件和流體域在自由液面處的邊界條件:
流體域無量綱形式的流體動力學方程:δφ=0
流體域在固體壁面處的邊界條件:
流體域在自由液面處的邊界條件:
(2.6)、將步驟(2.5)中的三個方程寫成galerkin變分形式方程:
式中:sw表示固體壁面,sf代表自由液面,v表示流體域δφ表示對φ取變分。
(2.7)、將步驟(2.6)中的方程前兩項進行高斯變換,並將液體在自由液面處的邊界條件簡化為獲得:
(2.8)、對流體域劃分三維實體網格,在每個單元內有:
其中代表φ在單元結點j處的值,nj為第j個單元的單元插值函數,ne為單元結點數。
(2.9)、將步驟(2.8)所得到φ代入至步驟(2.7)的公式中,根據變分的任意性推導得到單元剛度陣和單元質量陣:
單元剛度陣:
單元質量陣:
式中,j∈[1,ne],k∈[1,ne]。
(2.10)、基於(2.9),結合(2.8)劃分的三維網格,利用有限元分析方法將單元剛度陣和單元質量陣組裝成為整個流體域的液體剛度矩陣和液體質量矩陣,整個流體域的液體剛度矩陣和液體質量矩陣,通過特徵值求解方法獲得n階ωi、φi和模態坐標qi,i∈[1,n],所述n≥1。
(2.11)、計算流體域液體晃動的n階固有頻率ω0i和模態φi為:
(3)、假設液體在微重力的作用下發生晃動,基於球形貯箱零重力環境下液體晃動的n階固有頻率ω0i和模態φi,推導貯箱內液體晃動時液體施加於貯箱壁面的作用力和液體相對貯箱晃動的動能,並依據其與步驟(1)中建立的等效力學模型作用力和動能等效原則,計算得到步驟(1)中所建立等效力學模型的晃動質量ms和靜止質量m0。
(3.1)、定義參考坐標系o0xyz和obxyz分別為慣性坐標系和貯箱本體坐標系,假設本體坐標系原點ob與球心oc重合,將勢函數描述成:
式中,r為某液體質點相對於ob點的矢徑,rb是ob相對於o0的矢徑,φi和qi分別為第i階液體晃動模態和模態坐標,n為參與計算的模態階數。
(3.2)、計算液體對貯箱的作用力:
(3.2a)、依據步驟(3.1)得到的勢函數形式,計算獲得流場動壓pd為:
為rb相對於時間變量t的二階倒數,為模態坐標qi相對於時間變量t的一階倒數。
(3.2b)、依據流場動壓pd,計算液體對貯箱的作用力:
其中,n為貯箱壁面處的外法向單位矢量,mliq為流體域液體質量。
(3.3)、計算液體相對於貯箱晃動的動能:
(3.3a)、依據步驟(3.1)得到的勢函數定義,獲得流體速度u:
(3.3b)、計算液體相對於貯箱的動能:
(3.4)、計算等效力學模型產生的作用力和動能,採用步驟(2)所述的等效力學模型時,貯箱受到的作用力fe和等效力學模型相對於貯箱運動的動能te分別表示為:
式中,rs為晃動質量ms相對於oc點的矢徑。
(3.5)、將步驟(3.3)和步驟(3.4)中獲得的作用力和動能進行等效,即:f=fe、t=te,得到晃動質量ms和靜止質量m0的表達式為:
m0=mliq-ms
(3.6)、根據晃動質量ms、靜止質量m0和流體域液體晃動的第1階固有頻率ω01,確定彈簧阻尼器的剛度係數ks和阻尼係數cs::
ks=msω012
考慮粘性耗散作用,所述液體晃動阻尼比根據貯箱壁面邊界層內和液體內部的平均能量耗散率dw和di得到:
其中分別代表貯箱壁面邊界層內(即貯箱壁面至液體速度達到0.99倍主流速度的流體區域內)和液體內部的平均能量耗散率。式中,ν為液體的粘度,u代表貯箱壁面附近的流體速度,r(φ)表示為
這種建模方法與常重力環境下的彈簧-質量等效建模方法有很大區別。一方面,常重模型用來描述液體質心相對於貯箱的水平振動,因此通常包含水平方向上兩個晃動方向互相垂直的的彈簧-質量系統,晃動質量共具有兩個自由度;而三軸彈簧-質量模型可用來描述液體沿任意方向的運動,晃動質量具有三個自由度。另一方面,常重建模方法中由重力提供回復力,液體晃動的固有頻率近似與成正比;而對於微重力環境,表面張力可以提供的回覆作用很微弱,因此液體呈現出較弱的振動特性,其固有頻率由表面張力係數決定。
實施例:
球形貯箱半徑為r=0.547m,充液比為25%,液體為常溫下的水。通過計算獲得其等效彈簧-質量模型,ms=102.8kg,m0=68.48kg,ks=0.14425n/m,cs=0.2827ns/m。
貯箱球心在本體坐標系下的坐標為(0.3,0.4,0.5)m,施加給貯箱沿x軸方向的平動激勵和繞x軸方向的轉動激勵,運動規律分別為x=0.01sin(0.1πt)m和θx=0.01sin(0.2πt)rad。重力加速度沿z軸負向,大小為g=10-5m/s2。獲得液體對貯箱的作用力如圖4和如5所示。圖4和圖5同樣畫出了利用商用軟體flow-3d在同樣的激勵條件下計算同樣的貯箱的響應。對比結果表明,誤差小於10%。採用本方法計算獲得液體對貯箱的作用力耗時僅十多分鐘,而採用flow-3d計算需要數小時。
本發明未詳細描述內容為本領域技術人員公知技術。
