考慮外力衝擊幹擾和阻尼的多足機器人能量裕度計算方法與流程

2023-05-20 13:17:31 2

本發明涉及機器人穩定性領域，具體涉及一種考慮外力衝擊幹擾和阻尼的多足機器人能量裕度計算方法。

背景技術：

近年來，隨著機器人技術日益成熟，在探險、焊接、太空、搬運、服務方面得到非常廣泛的應用。多足機器人是一個複雜的機電一體化系統。作為被控對象，其本身是一個高度非線化、多變量、多參數耦合的複雜系統，使對其穩定性控制變的尤為困難。因此機器人穩定性控制問題成為近年來研究的熱點問題。

機器人在野外行走，六足機器人相對二足、四足機器人而言，具有更豐富的運動步態。且六足機器人具有冗餘的腿，機器人在複雜路面行走時，即使當一條腿或若干腿失效時，只要有三條腿能保持支撐狀態，機器人能繼續保持一定的運動能力。因此本發明以六足機器人在崎嶇地面上行走作為研究對像。

目前針對六足機器人在崎嶇地面上動態穩定性研究，通常採用是零力矩(ZMP)判定、壓力中心法(COP)，然而其只考慮了機器人的足端反力，考慮因素過少，且不能反映機器人的抗幹擾能力。傳統的能量穩定邊界法沒有考慮到機器人的機械震蕩屬性。而李雅普諾夫穩定性理論難於對時變、非線性化做出瞬時響應。因此，目前需要一種機器人穩定性判定的方法能實時監測機器人的穩定性，使機器人能快速做出調整，保持穩定的行走。

技術實現要素：

針對現有的穩定性判定方法存在考慮影響因素太少或時效性差的問題，本發明提出一種考慮外力衝擊幹擾和阻尼的多足機器人能量裕度計算方法。該算法主要依據重心位置、虛擬彈性阻尼、合力矩得出，最終用於機器人在複雜路面行走時因外力衝擊和自身慣性力矩作用，判定是否發生傾覆，以確保機器人穩定的行走。最終提出一種能適用於多種地形，且時效的穩定性計算方法。

本發明解決其技術問題所採用的技術方案是：

一種考慮外力衝擊幹擾和阻尼的多足機器人能量裕度計算方法，包括如下步驟：

步驟一：把機器人的翻轉動作轉換為包含彈簧阻尼特性的機械旋轉系統，計算機器人的能量裕度表達式；

步驟二：建立機器人在笛卡爾坐標系下的D-H數學模型；

步驟三：結合步驟二解析機器人能量裕度函數所需有關參數。

進一步，所述的步驟一通過以下方式實現：

1.1)根據牛頓第二定律列出機器人的動力學微分方程：

其中，將繞邊線翻轉時的機器人，視為一個機械旋轉系統，該系統由轉動慣量為Ji、扭轉剛度為KS和粘性阻尼係數為C的阻尼器組成；

1.2)求解機器人繞邊線旋轉的實時重心處合力矩，即驅動力矩：

式中，MGi為實時重心處重力相對旋轉邊線產生的力矩；MI為實時重心處的等效慣性力矩；Mri為著地腳因支撐力產生的力矩；fi為各足端豎直向上的力；θi為直線AB與水平面夾角，δi為重心繞邊線旋轉角度；θ為斜線傾角；ri為各足端到旋轉邊線的距離；ei為旋轉邊線的單位法向量，以支撐多邊形逆時針方向為正方向；

1.3)係數KS、C測定，根據上述的機械旋轉系統整理得

兩邊進行拉氏變換，求得其傳遞函數為：

因此求得

式中，TC、TS分別為當機器人受到一個脈衝力時，機械旋轉系統的震蕩周期與穩定時間；

1.4)求解機器人考慮外力衝擊幹擾和阻尼的能量裕度

機器人繞邊線旋轉到最高點的勢能變化：

機器人繞邊線旋轉到最高點的動能變化：

當w0為正時：

當w0為負時：

假設機器人繞邊線旋轉到最高點時wi＝0，因此求得機器人當前位置因外界幹擾不發生完全側翻，所能抵抗的能量為：

Ei＝Vi-V0+Ki-K0

求得：

上述公式中，w0、MRi'分別為實時重心位置繞邊線旋轉的角速度與合力矩，方向延旋轉邊線，以支撐多邊形逆時針方向為正方向；

根據能量穩定裕量的概念可知，定義能量穩定裕度為SEm，設最小穩定裕度SE，當SEm≥SE時，機器人能穩定工作。

再進一步，所述的步驟二通過以下方式實現：

在機器人的各關節處與軀體中心，建立笛卡爾坐標系，設坐標系C到坐標系O的之間的旋轉變換為線性變換為OPC，因此求得C到O坐標系的齊次變換為：

當空間有n個坐標系時，若已知相鄰坐標系之間的齊次變換矩陣，則：

M0n＝M01·M02·…Mn-1n

其中Mij為相鄰坐標系的齊次變換，由此建立機器人各部分在坐標系O中的位置。

更進一步，所述的步驟三通過以下方式實現：

4.1)重心位置參數，

假設各部件均為勻質材料，因此其重心均在其幾何中心處，根據步驟二中齊次變換矩陣，求各部件重心在世界坐標系的位置；

以軀體重心在世界坐標系中的位置求解為例：

式中，表示軀體重心在坐標系OC中的位置；

同理求得各部件重心在O的位置，根據各重心位置坐標代入相關公式求得實時重心位置；

4.2)求解實時重心繞支撐邊線旋轉到最高位置的豎直位移；

設構成傾翻邊線的兩足端位置坐標：

A(xA,yA,zA)，B(xB,yB,zB)

首先，由幾何關係式，求直線AB的表達式與重心CG到直線AB的距離Hi；

再次，求重心繞AB旋轉到最高點的豎直位移；

SNEi＝ECG'cosθ＝Hi(1-cosδi)cosθi

式中θi為直線AB與水平面夾角，δi為重心繞邊線到最高點的旋轉角度；

最後把解析出的相關參數代入到能量裕度函數中，求得機器人穩定裕度值，用於穩定性判定，保證機器人穩定工作。

本發明的有益效果主要表現在：

1、本發明考慮了機器人穩定行走的動態影響因素，包括角速度、力矩等。並在求解重心位置的能量裕度基礎上，考慮機器人自身的彈簧阻尼特性，此方法能最大程度的計算出機器人能量穩定裕度。

2、考慮外力衝擊幹擾和阻尼的多足機器人能量裕度計算方法，能適用於多足機器人在複雜地形上行走時的動態穩定性分析，使機器人具有一定抵抗外力衝擊的能力。

附圖說明

圖1是本發明的考慮外力衝擊幹擾和阻尼的多足機器人能量裕度計算方法，所應用的六足機器人結構示意圖。

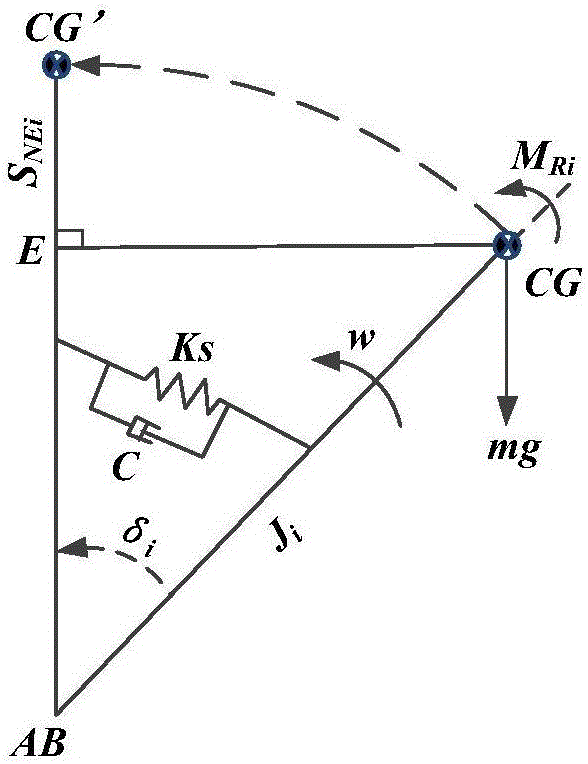
圖2是六足機器人繞邊線等效的機械旋轉系統示意圖。

圖3是六足機器人在斜面行走示意圖。

圖4是六足機器人的單腿D-H模型。

圖5是本發明的考慮外力衝擊幹擾和阻尼的多足機器人能量裕度計算方法的流程圖。

具體實施方式

下面結合附圖對本發明作進一步描述。

參照圖1～圖5，一種考慮外力衝擊幹擾和阻尼的多足機器人能量裕度計算方法，以六足機器人為例，包括機器人軀體和六條相互對獨立的步行腿，所述計算方法包括以下步驟：

步驟一：把機器人的翻轉動作轉換為包含彈簧阻尼特性的機械旋轉系統，計算機器人此時的能量裕度表達式；

1.1)根據牛頓第二定律可列出機器人的動力學微分方程：

其中，將繞邊線翻轉時的機器人，視為一個機械旋轉系統，該系統由轉動慣量為Ji、扭轉剛度為KS和粘性阻尼係數為C的阻尼器組成。

1.2)求解機器人繞邊線旋轉的實時重心處合力矩，即驅動力矩：

式中，MGi為實時重心處重力相對旋轉邊線產生的力矩；MI為實時重心處的等效慣性力矩；Mri為著地腳因支撐力產生的力矩；結合圖3中所示，fi為各足端豎直向上的力；θi為直線AB與水平面夾角，δi為重心繞邊線旋轉角度；θ為斜線傾角；ri為各足端到旋轉邊線的距離；ei為旋轉邊線的單位法向量，以支撐多邊形逆時針方向為正方向。

1.3)係數KS、C測定方法，根據上述的機械旋轉系統整理得

兩邊進行拉氏變換，求得其傳遞函數為：

因此求得：

式中，TC、TS分別為當機器人受到一個脈衝力時，機械旋轉系統的震蕩周期與穩定時間。

1.4)求解機器人的考慮外力衝擊幹擾和阻尼的能量裕度

機器人繞邊線旋轉到最高點的動能變化：

當w0為正時：

當w0為負時：

假設機器人繞邊線旋轉到最高點時wi＝0，因此機器人求得當前位置因外界幹擾不發生完全側翻，所能抵抗的能量為：

Ei＝Vi-V0+Ki-K0

求得：

上述公式中，w0，MRi'分別為實時重心位置繞邊線旋轉的角速度與合力矩，方向延旋轉邊線，以支撐多邊形逆時針方向為正方向；

根據能量穩定裕量的概念可知，定義能量穩定裕度為SEm，其值越大，表示機器人越穩定。然而為了確保機器人在外力衝擊作用下安全可靠的工作，設最小穩定裕度SE，當SEm≥SE時，機器人能穩定工作。

有益於機器人在行走過程中，根據實時檢測的關節轉角與機身角速度等有關變量，計算當前能量裕度值，判定機器人是否能穩定行走。並建立適當的自適應控制算法，根據環境情況和系統狀態，優化關節驅動參數，保證機器人穩定工作。

步驟二：根據機器人的運動學，建立機器人在笛卡爾坐標系下的D-H數學模型。由於機器人的六條腿相互獨立，且完全相同。因此根據機器人單腿的D-H數學模型可推導出整機的D-H模型。

如圖4所示，首先分別在機器人單腿各關節處，以及機器人軀體中心，建立笛卡爾坐標系。再進行兩個坐標之間的齊次變換，以軀體坐標到世界坐標系之間齊次變換為例：

上式為坐標系OC到ΣO旋轉變換，其中α、β、γ分別表示機器人在世界坐標系O下的機身姿態,且cα＝cosα，sα＝sinα，cβ,sβ,cγ,sγ依次類推。上述公式中的角度，分別由陀螺儀、關節舵機直接反饋得出。

OPC表示坐標系OC原點在O中相對位置。

上式為坐標系OC到O的平移變換

求得兩坐標之間的齊次變換:

當空間有n個坐標系時，若已知相鄰坐標系之間的齊次變換矩陣，則：

M0n＝M01·M02·…Mn-1n

其中Mij為相鄰坐標系的齊次變換，因此求出機器人各部分在坐標系O中的位置；

步驟三：本發明的考慮外力衝擊幹擾和阻尼的多足機器人能量裕度計算方法，與機器人的實時重心相關，為了計算方便，假設各部件均為勻質材料，即重心均在其幾何中心處，由此得出在其相應的笛卡爾坐標系中的位置，如圖4所示；

3.1)通過步驟二中求出的齊次變換矩陣，得出各部件重心在世界坐標系位置。

式中，表示軀體重心在坐標系OC中的位置

同理求得各部件重心在O的位置。代入以下公式求得機器人實時重心：

其中，W為機器人的總量，單位kg；n為機器人的足數，xo,yo,zo為機身重心在坐標系O中位置，xj,yj,zj為各部件重心在O中位置坐標

3.2)結合圖4求解實時重心繞支撐邊線翻轉時到最高位置時的豎直位移SNEi。

首先假設構成傾翻邊界的兩足端位置坐標：

A(xA,yA,zA)，B(xB,yB,zB)

求直線AB的表達式：

再次求重心CG到直線AB的距離為：

最後，通過直線與面的幾何關係，求重心繞AB旋轉到最高點的豎直位移：

SNEi＝ECG'cosθi＝Hi(1-cosδi)cosθi

式中，Hi為實時重心到支撐邊線的垂直距離；CG』為CG繞直線AB旋轉所能達到的最高高度點，δi為重心繞邊線的旋轉角度；θi為直線AB與水平面的夾角。最後把解析出的相關參數代入到能量裕度函數中，求得機器人穩定裕度值，用於穩定性判定，保證機器人穩定工作。