一種基於多模型的液壓作動器故障診斷方法與流程

2023-04-25 22:20:12

本發明屬於機械設備故障診斷領域，具體涉及一種基於多模型的液壓作動器故障診斷方法。

背景技術：
在飛機起飛、飛行及著陸的過程中，接收來自駕駛員的指令信號，帶動舵面偏轉，實現飛機的各種運動。因此，液壓伺服作動器(也稱液壓作動器)的性能與可靠性的好壞,對飛行控制系統乃至整個飛機的性能與安全至關重要。所以液壓作動器在飛行控制系統中通常認為是關鍵部件。然而其中的液壓作動器由於長期處於受力和不停地動作中，常常不可避免地出現各種故障而影響飛機正常飛行，可能引起一系列的連鎖反應，甚至出現重大事故，引起巨大的損失。在液壓作動器運行過程中,不可避免存在油液汙染、磨損等問題,容易造成液壓作動器的漸發性故障,這些漸發性故障的產生並不會馬上造成液壓作動器無法運行,但是會降低系統的效率與性能。針對系統的狀態進行及時有效的維護,不僅可以減少維護所需的投入資源,提高系統的利用率和可靠性,還能降低維護的成本。

技術實現要素：
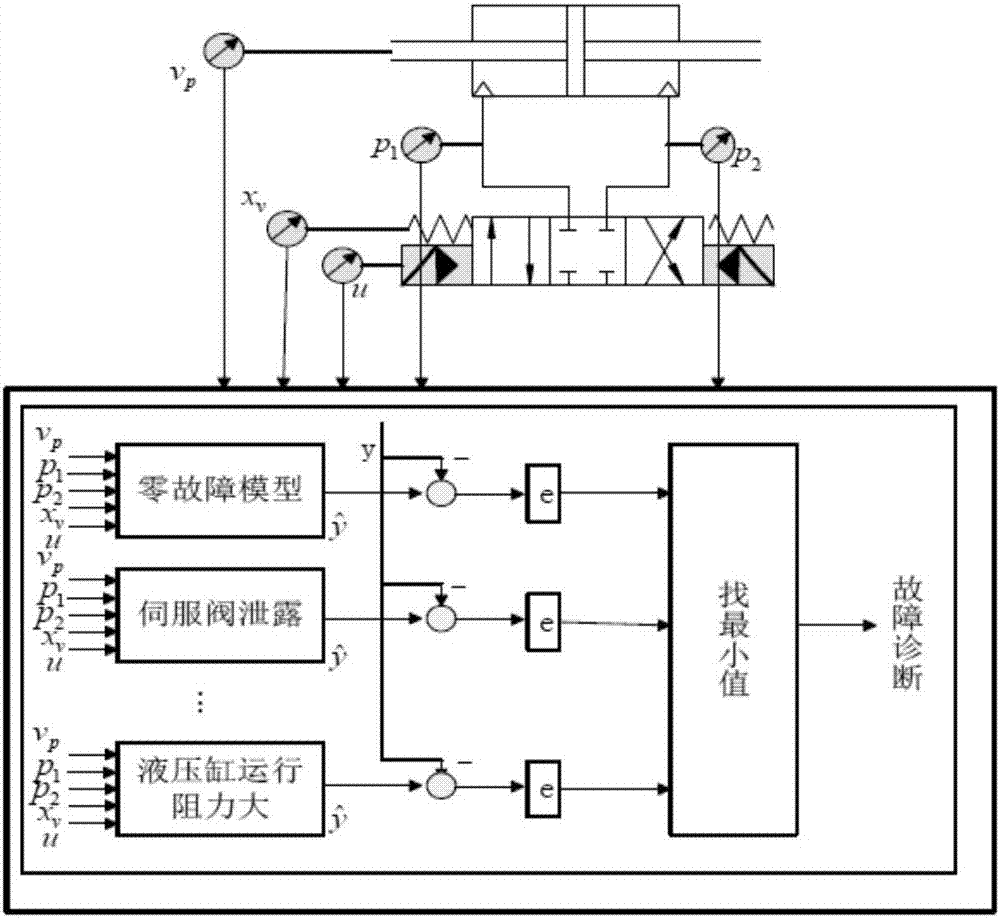
本發明的目的在於，針對液壓作動器可能出現的故障，提出一種基於多模型的液壓作動器故障診斷方法。本發明首先建立液壓作動器的狀態空間模型，然後根據故障類型建立能夠反映液壓作動器正常和故障情況的多個模型，將實際輸入代入各個模型，依次將實際輸出與各個模型的輸出利用積分型性能指標進行比較，殘差較小的模型所代表的情況即可反應液壓作動器的狀態。本發明提供了一種基於多模型的液壓作動器故障診斷方法，具體步驟如下：步驟一：建立液壓作動器的狀態空間模型；由液壓作動器各典型方程，通過合理選狀態變量建立狀態空間方程；步驟二：液壓作動器的多模型確定；故障引起液壓作動器狀態空間方程中某些參數改變，由此建立液壓作動器正常情況和各個故障模式下的參數矩陣；步驟三：實際輸入代入各個模型，得到殘差。將實際輸入代入各個模型，得到相應的模型輸出，並將實際輸出與各個模型輸出作差，得到殘差；步驟四：利用積分型性能指標判定液壓作動器狀態。在得到殘差後，代入積分型性能指標公式中，結果最小的一項所對應的情況即為液壓作動器當前的狀態。本發明的優點在於：1.狀態空間模型能夠描述液壓作動器內部信息的傳遞，由於液壓作動器的狀態空間模型中的參數都具有實際意義，因而參數矩陣的變化能夠代表液壓作動器的狀態變化情況，不同的參數能夠代表液壓作動器處於不同的工況。2.將實際輸出與各個典型工況下的狀態空間模型輸出依次帶入積分型性能指標公式，通過殘差比較能夠很容易的判斷出兩個模型間的差異大小。結果越小則說明相應的模型所代表的工況越接近液壓作動器當前狀態，從而實現液壓作動器的故障診斷。附圖說明圖1是現有技術中的液壓作動器的結構示意圖；圖2是利用多模型進行故障診斷的過程示意圖。具體實施方式下面將結合附圖對本發明的技術方案進行詳細說明。本發明針對的對象是由電液伺服閥和液壓缸構成的液壓作動器，如圖1所示，所述的液壓缸為雙出杆液壓缸，雙出杆液壓缸與電液伺服閥連接，在運行時，電液伺服閥(簡稱伺服閥)接收控制信號，將其轉換為閥芯的位移，使得雙出杆液壓缸中活塞兩側的油液產生壓力差，作動杆在壓力差的作用下進行運動，從而帶動舵面偏轉。本發明提供的基於多模型的液壓作動器故障診斷方法，具體步驟如下：第一步，建立液壓作動器的狀態空間模型：對於所述的液壓作動器，首先作出如下假設：①液壓作動器的供油壓力保持恆定，②伺服閥與液壓缸的連接管道對稱且足夠粗，管道中的壓力損失和管道動態特性忽略不計，③油液油溫保持不變，油溫為常數，④伺服閥的閥芯具有的理想的零開口和節流口是對稱匹配的，⑤伺服閥力矩馬達的非線性忽略。假設輸入給伺服閥的輸入電壓為u，伺服閥通常用一個一階環節來簡化描述伺服閥的動態特性，伺服閥的動態特性方程寫成微分方程形式為：式中:u--伺服閥輸入電壓，單位V；τ--伺服閥的時間常數；kp--伺服閥增益；xv--閥芯位移，單位m，--閥芯位移對時間的導數，單位m。假定四通滑閥節流口流出的液流為紊流狀態，令伺服閥閥芯位於中間位置時，即伺服閥中擋板組件沒有發生偏轉，閥芯位移xv＝0。當xv≥0時，液壓缸活塞向右推動，則依據閥口流量—壓力公式可得到流入液壓缸左腔流量q1及流出液壓缸右腔流量q2分別為：式中:q1--液壓缸左腔流量(m3/s)；q2--液壓缸右腔流量(m3/s)；Cd--節流口的流量係數；W--節流口的面積梯度(m)；ρ--油液密度(kg/m3)；ps--液壓作動器供油壓力(Pa)；po--液壓作動器回油壓力(Pa)；p1--液壓缸左腔壓力(Pa)；p2--液壓缸右腔壓力(Pa)。同理，當xv＜0時，液壓缸活塞向左推動，則依據閥口流量—壓力公式可得到流出液壓左腔流量q′1及流入液壓缸右腔流量q′2分別為：假定液壓缸的內外洩漏均為層流流動，液壓缸每個液壓腔內各處壓力相等。則依據可壓縮流體的連續性方程有：式中：V--所取液壓腔的體積(m3)；p--所取控制腔內的液體壓力(Pa)；t為時間；ΣqI--流入液壓腔的總流量(m3/s)，；∑qo--流出液壓腔的總流量(m3/s)；β--流體體積彈性模量((N/m2)Pa)。將可壓縮流體的連續性方程式(6)應用在液壓缸左右兩液壓腔中可理解為：流量流進液壓左腔的淨流量會等於流體被壓縮的流量與活塞運動所需的流量之和，即流入液壓缸左腔的流量q″1滿足如下關係等式：從液壓缸右腔流出的流量q″2滿足如下關係等式：式中:Ap--液壓缸活塞有效面積(m2)；xp--液壓缸活塞杆位移(m)；Cip--液壓缸內洩漏係數(m3/s·Pa-1)；βe--有效體積彈性模量(包括油液、混入油中的空氣、連接油管和缸體的機械柔度)(Pa)；V1--液壓缸左腔容積(包括閥口至液壓缸左腔油管和左腔的容積)(m3)；V2--液壓缸右腔容積(包括閥口至液壓缸右腔油管和右腔的容積)(m3)；其中液壓缸左右兩腔容積為：V1＝VL1+V01+Apxp(9)V2＝VL2+V02-Apxp(10)式中：VL1--閥口至液壓缸左腔的油管容積(m3)；VL2--閥口至液壓缸右腔的油管容積(m3)；V01--液壓缸左腔的初始容積(m3)；V02--液壓缸右腔的初始容積(m3)；xp--液壓缸活塞的位移(m)。液壓缸及負載主要受到的負載力包括慣性力、粘性摩擦力，則液壓缸輸出力與負載力的平衡方程為：式中：mt--活塞及負載折算到活塞上的總質量(kg)；Bp--活塞及負載的粘性阻尼係數(N/(m/s))。選取閥芯位移xv與液壓缸活塞杆速度vp、液壓缸左右兩腔壓力p1與p2為閉環系統的狀態變量，即：x＝[x1x2x3x4]T＝[xvvpp1p2]T(12)綜合併整理上述伺服閥動態特性方程、伺服閥的負載流量方程、液壓缸流量連續性方程、系統力平衡方程等基本方程，可建立電液位置伺服系統的狀態空間模型為：液壓作動器的輸出響應為液壓缸活塞杆速度，則輸出方程為：y＝Cx＝[0100][x1x2x3x4]T(14)液壓作動器的輸入為伺服閥輸入電壓u，則液壓作動器的狀態方程為：或矩陣A如下(xp≥0)：f(x,u)定義如下：則液壓作動器的狀態方程變換為：第二步，液壓作動器的多模型確定。液壓作動器中各個元部件的參數取值如表1所示。表1系統各參數取值矩陣A能夠作為反映液壓作動器系統狀態的模型。基於測量過程解算得到的參數建立幾組模型，即從獲得的狀態變量x、輸入向量u和輸出向量y，根據狀態空間方程解得矩陣A，其中一組模型描述零故障情況，其他模型描述某一種故障的發生過程，這些模型作為理論模型與實際模型進行比較。理論模型和實際模型的矩陣之間的差異能夠反映實際液壓作動器的狀況，若殘差越小，則越接近這個矩陣所代表的液壓作動器狀態，從而確定液壓作動器處於哪一種狀態。將已有的液壓作動器參數帶入系統矩陣A，同時為了能夠簡便、統一地表示液壓作動器狀態，將kp放入矩陣A的第一行第二列，得到液壓作動器在正常運行時的矩陣A為：在對液壓作動器進行故障機理分析後可知，液壓作動器的故障可以通過建立準確的數學模型基礎上改變物理參數或結構參數來模擬液壓作動器故障。如可以通過修改伺服閥增益和時間常數、液壓缸的內洩漏係數和外洩漏係數、油液體積彈性模量、液壓缸負載的粘性摩擦係數等來模擬系統故障。結合實際情況，表2為本實施例選擇要研究的液壓作動器的部分典型故障，及其物理參數改變設置。表2仿真實現部分典型故障類型根據仿真和實際運行經驗，矩陣中有些參數在液壓作動器正常和故障時的變化很小，這些參數包括活塞、活塞杆、油液及負載總質量mt、活塞有效作用面積Ap、閥口面積梯度W和孔口流量係數Cd，這些參數對狀態變量的變化影響很小，將它們作為常數。當液壓作動器正常運行時，將常數量帶入公式(16)矩陣A，得到液壓作動器系統矩陣A1：當液壓缸存在內洩露時，設置活塞與缸筒間隙為1mm，通過仿真得知內洩露會使計算得到的Bp變小，Bp＝12000，此時液壓作動器系統矩陣A2為：當液壓缸運行阻力大時，設置負載及活塞的粘性摩擦係數為20000(N/(m/s))，此時液壓作動器系統矩陣A3為：當系統油液混入空氣時，油液混入空氣會使油液體積彈性模量變小，設置βe＝5×108Pa，此時液壓作動器系統矩陣A4為：當伺服閥洩露時，伺服閥增益kp會減小，此時液壓作動器系統矩陣A5為：當伺服閥堵塞時，伺服閥的時間常數τ會增大，此時液壓作動器系統矩陣A6為，第三步，將實際輸入代入各個模型，即液壓作動器系統矩陣A1～A6，得到多個輸出。第二步中得到的多個模型能夠代表系統的6個典型工作狀態(式20～式25)，在得到液壓作動器的實際輸入後，將實際輸入依次代入到各個模型，得到6個模型對應的輸出這個過程如圖2所示。第四步，利用積分型性能指標判斷故障。利用如下所示的積分型性能指標，能夠合理避免突變的誤差，提高判斷的準確性：其中，ei(t)為模型誤差，即實際輸出與各個理論的模型輸出的差值，c1＞0和c2＞0分別為暫態和記憶加權因子，合理選擇c1和c2可使瞬時誤差和累積誤差保持合適比例，λ＞0為遺忘因子，表示對性能指標的記憶效果並確保J(t)有界。遺忘因子的合理選擇可以部分消除初始狀態偏差,外部幹擾等因素的影響。根據試湊法選擇合理的c1、c2、t0、λ和τ後，將步驟三中得到的和y(t)代入上面兩個式子(式26和式27)，在每一時刻，指標中結果最小的一項中所代表的狀態即為液壓作動器系統當前的狀態。