一種攝像機標定方法與流程
2023-04-26 03:39:01 2
本發明涉及一種攝像機標定方法,特別是涉及一種適用於交通視頻的一種攝像機標定方法。
背景技術:
視頻檢測技術在交通信息檢測中有著重要的應用,主要利用圖像處理技術對獲取到的交通視頻圖像進行一系列處理,提取出有用的信息,完成交通參數、交通狀況和交通事件的檢測,是ITS(Intelligent Transportation System)中的一個熱點研究方向。視頻檢測技術在攝影測量、計算機視覺等領域的應用,一個基本的問題是攝像機的標定問題。在實際的圖像視頻處理中為確定實際空間物體的三維坐標與圖像上的對應點的映射關係,需要通過建立相應的幾何模型,求解幾何模型的參數,幾何模型的參數就是攝像機參數,這個參數的求解過程成為攝像機的標定。在視頻檢測技術中,攝像機的標定時最基礎的和最重要的一步,它的精度和準確度直接影響後續工作的結果。因此提高攝像機標定的準確度和算法的簡潔度是研究工作的重點所在。
攝像機的標定可以採取在特定的試驗條件下,基於形狀、尺寸已知的參照物,利用圖像變換和數學計算的方法來獲得攝像機的參數,成為傳統的攝像機標定方法。此類標定方法大體有以下幾種:利用最優化算法的標定方法,典型代表有攝影測量學中的傳統方法和線性變換方法;利用攝像機變換矩陣的標定的方法;考慮畸變補償的兩步法;雙平面方法;改進的張正友標定法等。這些方法利用特定的參照物獲得實際空間物體與圖像上對應點的映射關係,算法簡單,但有一定的試驗條件要求。
此外,還可以採取不依賴參照物,利用不同幀圖像上物體之間的對應關係的方法進行標定,即自標定方法。主要有利用絕對二次曲線和極線變換性質解Kruppa方程的攝像機自標定方法;基於二次曲面的自標定方法;基於主動視覺的攝像機自標定技術等。此類方法靈活實用,但精度有待進一步提高。
技術實現要素:
本發明要解決的技術問題是提供一種簡單易行,計算量小的攝像機標定方法。
本發明採用的技術方案如下:一種攝像機標定方法,具體方法為:利用路面上標線作為參照物,根據攝像機成像原理抽象出交通視頻中的像素行和路面實際距離之間的幾何模型,對幾何模型進行解析,得到視頻圖像上像素行和實際路面的距離映射關係。
建立幾何模塊的具體方法為:
建立幾何模型基準,由公路路面上架設的攝像機採集到的視頻原圖像為基準,畫定N個點,畫定的點之間的距離在實際路面上的距離相等,形成N-1個像素段;取每個像素段的下端點分別向下和上延伸代表圖像上的像素段變化;所述N大於等於3;
建立幾何模型,以每個像素段的下端點分別向下和上延伸代表圖像上的像素段形成2(N-1)個不同的求解區域。
所述N=3,3個點形成兩個像素段m和n;它們在實際路面上的距離是相等的。取n段的下斷點分別向下和上延伸代表圖像上的像素段的變化,取m的上端點分別向下和上延伸代表圖像上的像素段的變化,形成4個不同的求解區域:區域①、②、③和④;設L為延伸像素段,K為當L移動時對應的路面實際距離的變化量。
m,n表示視頻圖像上的兩個像素段,這兩個像素段對應的實際距離相等,假設都是A;在區域①裡,L表示在視頻圖像上以n的下端點為基準向下延伸的像素段;在區域②裡,L表示在視頻圖像上以n的下端點為基準向上延伸的像素段;在區域③裡,L表示在視頻圖像上以m的上端點為基準向下延伸的像素段;在區域④裡L表示在視頻圖像上以m的上端點為基準向上延伸的像素段。K為當L移動時對應的路面實際距離的變化量,m和n所代表的路面實際距離相等,L變化的同時K也跟著做相應的變化。
對幾何模型進行分析的具體方法為:在視頻上找一個點M,M點所對應的路面上的點為N,視頻圖像中像素距離MD所對應的實際距離NA,O點為攝像機的焦點,NC為實際路面中的車道線,MF為攝像機拍攝的交通視頻圖像中對應的車道線,ON、OA、OB和OC是攝像機管線,D、E和F是選擇的三個點,n=DE,m=EF,對應的實際路面分別是AB和BC,其中AB=BC=h;對區域①進行求取,得到
即:
同理,求取其他幾個區域的結果為:
區域②:
區域③:
區域④:
與現有技術相比,本發明的有益效果是:利用路面上標線作為參照物,提供一種線性模型下的攝像機幾何標定方法,該方法根據攝像機成像原理抽象出幾何模型,推算出圖像像素段變化時對應的路面實際距離變化的函數關係式,不用考慮攝像機內部參數,幾何推導出外部參數,簡單易行,計算量小。
附圖說明
圖1為本發明其中一實施例的幾何模型示意圖。
圖2為圖1所示實施例中的幾何推導示意圖。
具體實施方式
為了使本發明的目的、技術方案及優點更加清楚明白,以下結合附圖及實施例,對本發明進行進一步詳細說明。應當理解,此處所描述的具體實施例僅用以解釋本發明,並不用於限定本發明。
本說明書(包括摘要和附圖)中公開的任一特徵,除非特別敘述,均可被其他等效或者具有類似目的的替代特徵加以替換。即,除非特別敘述,每個特徵只是一系列等效或類似特徵中的一個例子而已。
如圖1所示,建立幾何模型基準,由公路路面上架設的攝像機採集到的視頻原圖像為基準,畫定3個點,畫定的點之間的距離在實際路面上的距離相等,形成2個像素段m和n;取n段的下斷點分別向下和上延伸代表圖像上的像素段的變化,取m的上端點分別向下和上延伸代表圖像上的像素段的變化,形成4個不同的求解區域:區域①、②、③和④;設L為延伸像素段,K為當L移動時對應的路面實際距離的變化量。
m,n表示視頻圖像上的兩個像素段,這兩個像素段對應的實際距離相等,假設都是A;在區域①裡,L表示在視頻圖像上以n的下端點為基準向下延伸的像素段;在區域②裡,L表示在視頻圖像上以n的下端點為基準向上延伸的像素段;在區域③裡,L表示在視頻圖像上以m的上端點為基準向下延伸的像素段;在區域④裡L表示在視頻圖像上以m的上端點為基準向上延伸的像素段。K為當L移動時對應的路面實際距離的變化量,m和n所代表的路面實際距離相等,L變化的同時K也跟著做相應的變化。
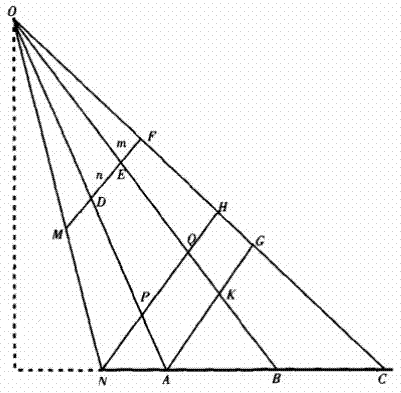
如圖2隨時,在視頻上找一個點M,M點所對應的路面上的點為N,視頻圖像中像素距離MD所對應的實際距離NA,O點為攝像機的焦點,NC為實際路面中的車道線,MF為攝像機拍攝的交通視頻圖像中對應的車道線,ON、OA、OB和OC是攝像機管線,D、E和F是選擇的三個點,n=DE,m=EF,對應的實際路面分別是AB和BC,其中AB=BC=h。做兩條輔助線:AG和NH,且AG和NH分別平行於MF。已知條件為:DE、EF和MD像素距離已知;AB=BC,並且都已知;MF平行於NH平行於AG。求NA的實際距離。求解過程如下:
對區域①進行求取,
由MF平行於AG,得出
可以得出
由MF平行於NH,得出
可以得出
將AK、NP和QH帶入下面兩式:
由ΔABK~ΔNBQ,得出即
由ΔACG~ΔNCH,得出即
得到
此時,兩個關係式中只有兩個變量,NA和解此二元一次方程得到
即:
同理,求取其他幾個區域的結果為:
區域②:
區域③:
區域④:
