一種基於四程中繼跟蹤模式的遠月面著陸器精密定位方法與流程

2023-05-28 18:06:46 1

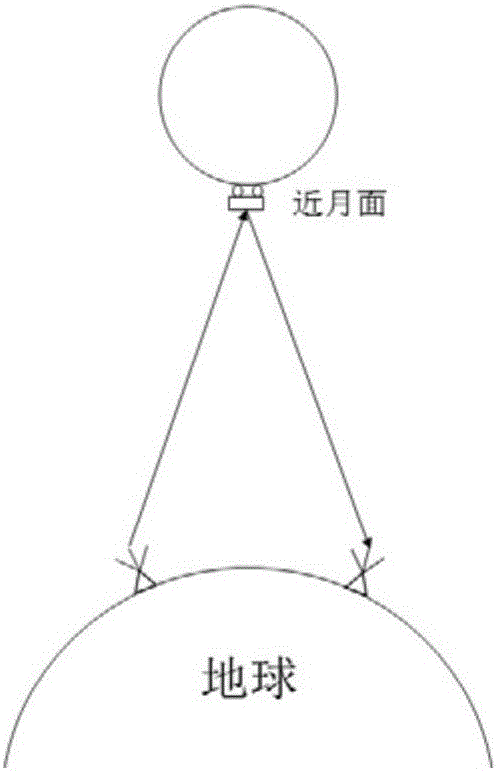
本發明屬於月球著陸器精密定位與深空探測領域，特別是涉及一種基於四程中繼跟蹤模式的遠月面著陸器精密定位方法。

背景技術：

目前，深空探測是世界各國競相爭逐的熱點，進行深空探測，可以進一步解答地球如何起源與演變、行星和太陽系形成和演化的過程、人類是不是宇宙中唯一的智慧生命、地球的未來將如何等一系列問題，同時有利於人類積極開發和利用空間資源。在深空探測中，探測器的定軌定位是任務成敗的關鍵，也是各種科學任務順利進行的前提。精密的探測器軌道是進行地形地貌測繪的基礎數據，也可以用於行星重力場的解算，進而反演行星的內部構造。

月球背面的著陸探測一直是國際上的熱點和難點。月球背面具有不同於月球正面的獨特地質構造，是研究地月起源的重要突破口；月球背面沒有地球電磁波幹擾，是進行低頻射電天文觀測的天然理想場所。但是由於月球自轉與公轉同步，月球背面著陸器無法與地球測站進行直接通信，任務難度和風險比較大，目前對月球背面的就位探測仍舊是一項國際空白。因此，開展月球背面的就位探測具有重要的科學意義和工程意義。

對於近月面著陸器的定位問題，一般採用運動學統計定位方法，採用測量模式包括：雙程/三程測距、測速，VLBI時延/時延率模型等等。在「嫦娥三號」著陸器的精密定位中使用了運動學統計定位方法，綜合了測距、測速數據和VLBI時延、時延率數據，著陸器定位的絕對精度在10m左右(曹建峰,張宇,胡松傑,等.2016.嫦娥三號著陸器精確定位與精度分析.武漢大學學報(信息科學版),41(2):274-278.doi:10.13203/j.whugis20140123.)，「玉兔號」漫遊器與著陸器的相對定位採用了同波束VLBI技術，相對位置精度可達到米級(黃勇,昌勝騏,李培佳,等.2014.「嫦娥三號」月球探測器的軌道確定和月面定位.科學通報,59(23):2268-2277.)。

但是對於月球背面著陸器的精密定位問題，如圖1所示，圖1a為近月面示意圖，圖1b為遠月面示意圖，由於月球自身的遮擋，遠月面著陸器與地球深空測控站無法通視，傳統的直接測量模式，如「嫦娥三號」中的雙程、三程測距/測速，VLBI時延/時延率測量模式將不再適用，因此有必要採取新的跟蹤測量模式對遠月面著陸器進行定位。

在對月球著陸器定位的過程中，涉及到坐標系的轉換。地面測站位於地球，一般用地球參考框架描述；月球著陸器需要用月球主軸坐標系來表示；而信號在太空中的傳輸要考慮大天體引力時延以及相對論效應的影響，最終均需要在太陽系質心坐標系下(BCRS)表示。為了得到高精度的定位結果，需要不同坐標系之間進行高精度的轉換。各坐標系之間的轉換如圖2所示。

地面測站坐標由協議地固系(ITRS)轉為J2000地球慣性坐標系下的坐標，此轉換需要歲差旋轉、章動旋轉、極移旋轉以及地球自轉旋轉。關於歲差、章動模型，隨著觀測值精度的不斷提高，也在不斷地修正。目前IERS2010規範推薦採用IAU2006決議的歲差章動模型。J2000地球慣性系坐標經過平移、洛倫茲變換可以轉到太陽系質心坐標系下。

同地固坐標系統的轉換中用到歲差章動和極移一樣，從月球主軸坐標系(PA)到月心天球坐標系，要考慮月球天平動(Libration)的影響。目前用於月球物理天平動研究的主要手段仍然是對月雷射測距(LLR)，由月球自轉引起測距的變化，通過數值積分來求得月球自轉相應的三個歐拉角，通過旋轉三個歐拉角即可轉換到月心天球坐標系下，進一步經過平移、洛倫茲變換可以轉到太陽系質心坐標系(BCRS)下。

目前對月球背面的著陸一直是國際空白，月球背面的著陸最大的難題是克服信號被月球遮擋的影響，同時面臨無法實時測控跟蹤著陸器等難題。

技術實現要素：

本發明的目的是克服傳統直接跟蹤測量模式無法對遠月面著陸器進行定位的缺陷，提供一種基於四程中繼跟蹤模式的遠月面著陸器精密定位方法，該方法藉助於中繼星的中繼跟蹤測量，可以消除月球自身的遮擋，實現對遠月面著陸器的精密定位。

為達到上述發明目的，本發明的技術方案提供一種基於四程中繼跟蹤模式的遠月面著陸器精密定位方法，建立月球著陸器-軌道器的四程中繼跟蹤測量模式的觀測模型，基於觀測模型實現遠月面著陸器精密定位，

所述四程中繼跟蹤測量模式，將月球軌道器作為中繼星，使用月球著陸器和月球軌道器之間的鏈路進行測量，設地球跟蹤站Ti在時刻i發送一個上行的信號給月球軌道器，月球軌道器位置為Sj，時刻為j；經過轉發，信號傳送給月面著陸器，相應位置為Lk，時刻為k，Lk位於月球背面；月面著陸器再次轉發給在軌的月球軌道器，此時軌道器已經從Sj的位置運動至Sm，時刻為m；之後該信號下行至地球跟蹤站Tn，時刻為n；設時刻n、m、k、j、i分別相應的參與者記為Tn,Sm,Lk,Sj,Ti，則有以下4個幾何距離，

R1＝|X(Sm)-X(Tn)|

R2＝|X(Sm)-X(Lk)|

R3＝|X(Sj)-X(Lk)|

R4＝|X(Sj)-X(Ti)|

其中，X(j)為參與者j在太陽系質心坐標系下下的位置矢量；

四程中繼測距的觀測模型建立如下，

R＝(R1+c·RLTnm)+R2+R3+(R4+c·RLTij)+

c·[TDB(i)-UTC(i)]-c·[TDB(n)-UTC(n)]

＝c·[UTC(n)-UTC(i)]

其中，RLTnm為由參與者Tn發射信號到Sm的廣義相對論時延，RLTij為由參與者Ti發射信號到Sj的廣義相對論時延，UTC(n)和UTC(i)分別為時刻n和時刻i對應的協調世界時時標，R為四程中繼測距值，TDB(n)和TDB(i)分別為時刻n和時刻i對應的太陽系質心力學時，c為光速；

設在一個都卜勒積分周期內，起始時刻Ts和終止時刻Te各自對應的四程中繼測距值為Rs、Re，建立四程中繼測速的觀測模型如下，

其中，Tc為一個都卜勒積分周期，RR為四程中繼測速值。

而且，根據四程中繼跟蹤測量模式，將月球軌道器的軌道和遠月面著陸器的位置同時視為待估參數，採用精密定軌的方式進行解算，最後得到兩者的最佳估值。

而且，採用精密定軌的方式進行解算時，

計算四程中繼測距值R對遠月面著陸器坐標X(Lk)的偏導數HR公式如下，

按照上式計算積分起始時刻Ts和積分終止時刻Te分別對應的四程中繼測距值R對遠月面著陸器坐標X(Lk)的偏導數Hs和He，則四程中繼測速值RR對遠月面著陸器坐標X(Lk)的偏導數HRR為

將結果作為觀測時刻的觀測值對狀態向量的偏導數。

而且，將探測器軌道跟蹤數據文件分為多個觀測弧段，將初始參考軌道x0ref＝[r0v0 p0 q0]T中的中繼星的初始位置r0、初始速度v0以及力模型參數p0作為局部參數處理，記作x1，維數為m1；參數q0是遠月面著陸器位置坐標，將其作為全局參數處理，記作x2，維數為3；採用精密定軌的方式進行解算時，融合多個觀測弧段相應法方程，將非線性的方程線性化，使用迭代法求解。

本發明的有益效果：本發明基於四程中繼跟蹤模式，利用一顆中繼星，實現對遠月面著陸器的事後精密定位；由於基於四程中繼跟蹤模式建立了中繼星和遠月面著陸器間的聯繫，解決了地球深空站無法直接跟蹤測量遠月面著陸器的問題。由於該方式對著陸器以及中繼星有很強的幾何約束，將使精密定軌、定位的精度得到極大地提高。此外，隨著此模式觀測數據的增加，可將用於支持對月球自轉歐拉角，月球K2勒夫數以及月球重力場等反演，得到更為精確的月球物理模型，進而為了解月球的起源與演化，深入研究月球內部構造提供重要的科學數據。本發明還提出將遠月球著陸器坐標作為全局參數進行解算，理論上更為嚴密，可得到高精度的遠月面著陸器坐標。因此，本發明具有重要的科研價值和市場價值，是我國領先世界的重要研究項目。

附圖說明

圖1為傳統的雙程/三程測距、測速及VLBI模型示意圖，其中圖1a為近月面示意圖，圖1b為遠月面示意圖；

圖2為本發明涉及到的各類坐標系之間的轉換示意圖；

圖3為本發明實施例的基於月球著陸器-軌道器的四程中繼跟蹤測量模型示意圖。

圖4為本發明實施例的解算流程示意圖。

具體實施方式

以下結合附圖和實施例對本發明技術方案進行具體描述。

為便於實施參考起見，首先分別介紹本發明涉及的精密定軌原理和基於月球著陸器-軌道器的四程中繼跟蹤測量模式(4W L-O)的基本原理：

(1)精密定軌原理

本發明中涉及到的精密定軌理論不考慮探測器搭乘火箭被送入指定軌道的過程，而是進入指定軌道後，通過探測器自身發射無線電信號，建立與地面(或空間站和衛星)跟蹤測控系統的聯繫，從而對原始軌道進行調控和微分改進。具體闡述如下：

第一，根據牛頓運動定律，探測器(本文指月球軌道器)進入指定軌道(初始軌道)後，受到宇宙中各種力(天體引力、太陽光壓力等)的影響將會產生加速度，從而改變原有的初始運動狀態(初始軌道)。該過程可用一個常微分方程組描述，稱之為力模型。但由於太空環境複雜且人類目前的認知程度有限，不可能用該方程準確無誤地描述出探測器的實際受力情況，所以該方程組存在誤差即力模型存在誤差，具體體現在兩方面：第一，力模型中的已知參數不夠準確；第二，實際受力中還存在未建模的部分。對於第二點，需要整個科學的推動才能對受力有進一步的認識，所以力模型的誤差主要指第一點。

第二，如果不能對探測器保持聯繫，任何探測器都會很快失效。所以，探測器將會主動發射無線電信號，由地面(或空間站、衛星)跟蹤站的跟蹤測量設備進行接收。根據收發信號鏈路的幾何關係，可以建立相應的觀測模型。信號在實際傳播過程中，會受到複雜空間環境、相對論效應等的影響，該影響通常作為改正項融入觀測模型中，可以視為觀測模型的模型參數。同樣，由於對這些影響的認知有限等原因，這些模型參數也存在誤差。同時，跟蹤站的觀測設備本身存在一定的誤差，所以獲取的觀測資料也是存在誤差的。

結合上述兩點，精密定軌實際上可以這樣描述：利用帶有大量帶有誤差的觀測數據和並非精確的運動學微分方程，使用統計學原理解算在某種意義下的探測器初始軌道和相關模型(力模型、觀測模型)參數的最優估值的過程。

由於一般將觀測誤差視為正態分布的隨機誤差，所以精密定軌實質上為基於最小二乘的參數估計問題，即：尋找初始軌道和相關模型(力模型、觀測模型)參數的估計值，使得利用估計值計算的觀測殘差平方和最小。

其中，第一點中所述力模型的形式如下：

式(1)是一個描述力模型的常微分方程組，其中：x(t)為隨時間t變化的m維狀態向量，包含探測器的位置r(t)、速度v(t)、力模型相關參數p以及與觀測模型相關的參數q，m表示以上這些參數的個數的總和；為隨時間變化的m維狀態向量的一階導數，f(t,x(t))為的具體函數形式，x0為曆元初始時刻t0不精確的初值x(t0)，包含探測器的初始位置r0(t0)、初始速度v0(t0)、(以下簡寫為r0和v0)力模型相關初始參數p0以及與觀測模型相關的參數q0，如式(2)所示。

其中，

令z表示n維觀測向量，即：

zi(ti)表示第i個觀測量，即在觀測時間ti獲取的觀測量，i＝1,2,…n，n表示觀測弧段內的觀測次數；zi(ti)用於表示第i個觀測量與探測器狀態的關係如下：

zi(ti)＝gi(ti,x(ti))+εi＝hi(ti,x0)+εi (4)

式(4)中：gi表示觀測量與觀測時間ti及該時刻的探測器狀態x(ti)的函數關係；hi表示觀測量與觀測時間ti及曆元初始時刻t0的太空飛行器狀態的函數關係；εi為在觀測時間ti由於誤差造成的理論觀測量與實際觀測量的偏差。式(5)寫為向量表達式如下：

z＝h(x0)+ε (5)

其中，z,h(x0),ε分別為式(4)中所述的zi(ti),hi(ti,x0),εi的向量形式；一方面，h(x0)是一個關於未知矢量x0的非線性函數，利用最小二乘方法求解軌道確定問題非常複雜；另一方面，真實的矢量x0雖然未知，但是實際給出的初始探測器狀態可以視為探測器真實初始狀態x0的近似值，稱之為初始參考軌道，記為x0ref。在該點進行泰勒展開，並忽略高階項，稱之為線性化，可得：

寫為誤差方程的形式，有：

ε＝Δz-HΔx0 (7)

Δx0＝x0-x0ref (8)

Δz＝z-h(x0ref) (9)

式(6)至式(10)中：△x0為真實初始軌道x0與不精確的初始參考軌道x0ref的偏差；△z為實際觀測量z與利用該不精確的參考軌道x0ref計算的觀測量的殘差；H為利用曆元t0時刻參考軌道初值(即初始參考軌道x0ref)計算的觀測量相對於曆元t0時刻狀態向量的偏導數，x(ti)為曆元ti時刻的參考軌道，H可以利用鏈式法則進行展開成(10)式所示的形式。是ti時刻的觀測量對狀態向量x(ti)的偏導數。

通過線性化，精密定軌問題可以簡化為線性最小二乘問題。獲取狀態改正量△x0的最優估值△x0lsq，使得經狀態改正△x0後的目標函數J(Δx0)取最小值。

J(Δx0)＝εTε＝(Δz-HΔx0)T(Δz-HΔx0) (11)

根據線性方程理論，如果H滿秩，則目標函數取極小值的條件為

計算上述偏導數，可得法方程形式如下：

(HTH)Δx0＝HTΔz (13)

解得線性最小二乘問題解Δx0lsq的一般形式：

Δx0lsq＝(HTH)-1(HTΔz) (14)

矩陣HTH是一個m維對稱矩陣，通常稱為法方程矩陣。

如果在軌道估計之前，在已有待估參數△x0初始值的前提下，同時具備待估參數△x0的驗前信息

式(15)中，E(△x0)表示對△x0取期望，cov(△x0-x0)表示對某個隨機變量序列取方差-協方差矩陣；給出的先驗信息即為待估參數△x0的期望x0和方差-協方差矩陣P0。引入變量如下，

這樣式(11)所示的目標函數就可以寫為

相應的法方程可以寫為

其最小二乘解Δx0lsq為

則修正後的太空飛行器狀態x0lsq為

x0lsq＝x0ref+Δx0lsq (20)

對於不同觀測類型，測量數據精度各有差異。而上述式中將觀測數據按相同觀測精度處理，這在實際應用不盡合理，故需要對數據進行加權，相應的權矩陣可以寫為如下形式：

W＝diag(σ1-2,…,σn-2) (21)

σi為互不相關的測量誤差，i＝1,2,…n。當誤差相互關聯時，權矩陣為非對角矩陣。相應的法方程的形式為：

式(18)的最小二乘解為如下形式：

當不考慮先驗信息時，P0-1＝0；相應的法方程變為：

(HTWH)Δx0＝HTWΔz (24)

相應的最小二乘解為：

Δx0lsq＝(HTWH)-1(HTWΔz) (25)

其中，式中的H按照式(10)進行計算；式中的△z按照式(9)計算。

由於對非線性方程進行了線性化，為了保證最終解的準確性，根據精密定軌理論，整個過程需要迭代進行。即將解算得到的x0lsq重新作為x0ref，重複式(1)至式(25)，直至與上一次得到的x0lsq之差的絕對值小於設定的限差δ即可。

故本發明可概括為：結合一種新的觀測模型——四程中繼跟蹤測量模型，將月球軌道器(中繼星)的軌道和遠月面著陸器的位置同時視為待估參數，按照精密定軌的流程進行解算，最後得到兩者的最佳估值的過程。

(2)月球著陸器-軌道器的四程中繼跟蹤測量模式(4W L-O)原理

和傳統雙程模式相比，基於月球著陸器-軌道器的四程中繼跟蹤模式使用了著陸器和軌道器之間的鏈路。如圖3所示，地球跟蹤站Ti(時刻i)發送一個上行信號給月球軌道器(中繼星，下文軌道器均指中繼星)(位置為Sj，時刻j)，經過轉發，該信號傳送給月面著陸器(位置為Lk，時刻k，Lk位於月球背面)，著陸器再次轉發給在軌的月球軌道器(此時軌道器已經從Sj的位置運動至Sm，時刻為m)，之後該信號下行至地球跟蹤站Tn(時刻n)。上述過程就是基於月球著陸器-軌道器的四程中繼跟蹤模式信號收發的一個完整過程。在實際測量中，地球跟蹤站Tn可以通過積分都卜勒的方式得到4W L-O的距離變率，和雙程測速的模式類似。對於4W L-O測距和測速的理論值C的計算，和傳統的雙程測距測速類似，採用「回溯法」，即按照Tn-＞Sm-＞Lk-＞Sj-＞Ti的路徑，為便於計算，可視為有五個參與者Tn,Sm,Lk,Sj,Ti。地球跟蹤站Tn在n時刻接收到下行信號並記錄，但m，k，j，i時刻的相關參與者的狀態向量是未知的，需要進行光行時解算依次獲取。其中，光行時解算公式如下：

式(26)和式(27)中，c為光速；下標a為該支路的信號發射方，下標b為該支路的信號接收方；tb表示該支路的信號接收方的接收時刻，ta表示該支路的信號發射方的發射時刻；對於4W L-O模式的四條鏈路，a＝i時b＝j，a＝j時b＝k，a＝k時b＝m，a＝m時b＝n。式(26)中，rab是BCRS(Barycentric Celestial Reference System)坐標系下該支路信號發射方和接收方的幾何距離，是該支路信號傳播過程中的牛頓光行時，RLTab是該支路信號傳播過程中的廣義相對論時延。式(27)中，μs是太陽引力常數，μB是行星、外行星系統或月球的引力常數。γ為後牛頓參數，和代表該支路信號發射方和接收方分別在對應時刻的離太陽質心的幾何距離，和代表該支路信號發射方和接收方在對應時刻的離行星、外行星系統或月球質心的幾何距離。其中和代表該支路信號接收方和發射方在對應時刻的日心坐標向量，和代表該支路信號接收方和發射方在對應時刻的行星質心坐標向量。代表在日心坐標系下該支路信號接收方和發射方的幾何距離，代表在行星質心坐標系下該支路信號接收方和發射方的幾何距離。

本發明利用提出的月球著陸器-軌道器的四程中繼跟蹤觀測模型，同時結合傳統的雙程、三程測距測速觀測模式，實現中繼星的精密定軌和遠月面著陸器的精密定位。具體步驟如下：

根據式(2)，設與軌道器相關的初始狀態的近似值為：x0ref＝[r0 v0 p0 q0]T。其中，x0ref為隨時間變化的m維狀態向量，包含軌道器的初始位置r0、速度v0、力模型相關參數p0以及與觀測模型相關的參數q0；其中q0為遠月面著陸器的初始近似位置坐標同時，設置迭代收斂的限差δ，在設置迭代收斂的限差時，分別設置局部參數和全局參數迭代收斂的限差δ1和δ2。

①根據軌道器的實際受力情況，同時在給定的觀測站的觀測弧段內，選定x0ref，並將式(1)所示的微分方程組進行數值積分，解算出一條以x0ref為初始條件且並不精確的參考軌道xref(ti)，其中xref(ti)代表觀測弧段內某時刻ti的參考軌道xref，i＝1,2,…n。同時，式(10)所示的也可以由式(1)所示的微分方程組數值積分得來。具體實施時，初始值、微分方程組的具體細節以及限差可由本領域技術人員自行預先設定。

②建立月球著陸器-軌道器的四程中繼跟蹤測量模式(4W L-O)的觀測模型

本步驟相當於計算式(6)中的h(x0ref)。

四程中繼測距(4W L-O R)：

將下行信號到達Tn的時刻n記錄為協調世界時時標UTC(n)，協調世界時通常簡稱UTC，首先需要將該UTC時標轉換為太陽系質心力學時標TDB，可得到下行信號到達Tn的時刻的太陽系質心力學時標TDB(n)。之後通過光行時解依次得到Sm,Lk,Sj,Ti處對應的太陽系質心力學時TDB(m)，TDB(k)，TDB(j)，TDB(i)，最後再次通過時間轉換得到Ti處的協調世界時時標UTC(i)。在進行各個鏈路的光行時解算時，如式(26)和(27)所示，軌道器與地面之間的鏈路考慮廣義相對論時延項，軌道器與著陸器之間的鏈路由於距離很近，只考慮牛頓光行時，不考慮廣義相對論時延項。通過此「回溯」，可以得到相應時刻各個參與者的狀態向量。定義X(J)為參與者J在BCRS下的位置矢量，J＝Tn,Sm,Lk,Sj,Ti，那麼4個幾何距離依次為：

R1＝|X(Sm)-X(Tn)| (28)

R2＝|X(Sm)-X(Lk)| (29)

R3＝|X(Sj)-X(Lk)| (30)

R4＝|X(Sj)-X(Ti)| (31)

以上可作為四程測距測量方程。

至此，四程中繼測距(4W L-O R)的觀測模型建立如下：

其中，RLTnm和RLTij為式(26)和式(27)中的廣義相對論時延，即RLTnm為由參與者Tn發射信號到Sm的廣義相對論時延，RLTij為由參與者Ti發射信號到Sj的廣義相對論時延；UTC(n)和UTC(i)分別為上述Tn相應時刻n和Ti相應時刻i對應的協調世界時時標，TDB(n)和TDB(i)分別為時刻n和時刻i對應的太陽系質心力學時，R為四程中繼測距值，即基於月球著陸器-軌道器的四程中繼測距理論計算值。

四程中繼測速(4W L-O RR)：

基於月球著陸器-軌道器的四程中繼測速理論值按照積分都卜勒的形式可表達為：在一個都卜勒積分周期內，起始時刻Ts和終止時刻Te各自對應的四程中繼測距值Rs、Re之差相對於時間的變化率。首先將積分起始時刻Ts視為下行信號的到達時刻Tn，按照式(32)所示的觀測模型計算四程中繼測距值Rs，然後將積分終止時刻Te同樣視為下行信號的到達時刻Tn，按照式(32)所示的觀測模型計算四程中繼測距值Re。建立四程中繼測速(4W L-O RR)的觀測模型為：

上式中Tc為一個都卜勒積分周期，等於Te-Ts，RR為四程中繼測速值，即基於月球著陸器-軌道器的四程中繼測速理論值。

③計算觀測模型所得四程中繼測距觀測量(包括四程中繼測距值R、四程中繼測速值RR)對遠月面著陸器坐標的偏導數

本步驟相當於計算式(10)中的

四程中繼測距值R對遠月面著陸器坐標X(Lk)的偏導數HR：

按照式(34)計算積分起始時刻Ts和積分終止時刻Te分別對應的四程中繼測距值R對遠月面著陸器坐標X(Lk)的偏導數Hs和He，則四程中繼測速值RR對遠月面著陸器坐標X(Lk)的偏導數HRR為：

計算所得偏導數HRR即偏導數

④輸入實際觀測值序列(即n維觀測向量z)，按照式(9)計算Δz，並按照式(10)計算H矩陣。

⑤結合傳統的雙程/三程測距、測速等測量模型，結合實際測量精度，按照式(21)確定權矩陣W；其中，W也可以由本領域技術人員根據不同的算法(如：赫爾模特方差分量估計法)預先確定。

⑥生成如式(24)所示的法方程，根據式(25)解算出改正量Δx0lsq，根據式(20)計算出最佳估值，即修正後的太空飛行器狀態x0lsq。其中，x0lsq向量中包含有遠月面著陸器的位置坐標。

⑦將解算出的x0lsq作為①中的x0ref，重複①～⑥，直至兩次得到的Δx0lsq之差的絕對值小於預設的限差δ時停止迭代，得到最終的最佳估值x0lsq。

本發明進一步提出，在實際情況中，由於地球測站可視範圍有限，探測器變軌等原因，不能保證永遠有連續且有效的觀測跟蹤數據，所以探測器軌道跟蹤數據文件可分為多個觀測弧段；同時，根據待估參數本身的性質，一般將x0ref＝[r0 v0 p0 q0]T中的r0v0p0作為局部參數處理，記作x1，維數為m1，其中局部參數的特點是已知其每個弧段的初始近似值x1ref(i)，並解算每個弧段的參數的改正值Δx1lsq(i)，最終得到每個弧段的參數的最佳估值x1lsq(i)，其中，i＝n,n-1,…,1，代表第i個弧段；對於參數q0，本發明中指遠月面著陸器位置坐標X(Lk)，將其作為全局參數處理，記作x2，維數為3，其中全局參數的特點是與弧段無關，解算時融合多個弧段獲得最終的全局參數的改正值Δx2lsq以及最佳估值x2lsq。具體闡述如下：

對於每一個弧段，一般取1-2天的弧長。輸入某個弧段的初始近似值x0ref，綜合大量的四程中繼跟蹤測量值和傳統的雙程/三程測距、測速等測量值，對中繼星(軌道器)進行精密定軌，在不考慮參數先驗信息的前提下，按照步驟①～⑥，根據四程中繼跟蹤測量模式，針對單弧段中繼星精密定軌生成對著陸器坐標的偏導數，生成如式(24)所示的單弧段法方程，為了區分局部參數和全局參數，將法方程矩陣按照局部參數和全局參數的維數分塊，可得如下形式：

Δx1和Δx2分別代表待估的局部參數(包括中繼星初軌、力模型參數，中繼星初軌此處為位置和速度)的改正值和全局參數(即遠月面著陸器的位置坐標)的改正值，A11對應為局部參數的法方程矩陣，具體形式對應式(24)，為m1×m1維的矩陣A22對應為全局參數的法方程矩陣，具體形式對應式(24)，為3×3的矩陣A21和A12為矩陣分塊後的左下部分和右上部分；b1和b2按照式(24)所示對應為m1×1維的矩陣和3×1維的矩陣

為了更有效的解算待估參數，聯合多個弧段按照步驟①～⑥形成法方程，設有N個弧段可得到類似式(36)的一個序列的弧段法方程：

其中上標(1)～(N)表示弧段編號1～N。式(37)中各符號的具體含義與式(36)相同。

融合多個弧段的法方程，形成如下融合法方程：

對上式中的聯合矩陣每個弧段部分採取矩陣行變換，可得到如下形式：

式(38)和式(39)中的各項含義與式(36)相同，其中上標(1)～(N)表示弧段編號1～N。I代表單位矩陣，從下至上解算式(39)，首先解得全局參數向量的改正值Δx2lsq，即遠月面著陸器坐標的改正值，按照式(20)加到遠月面著陸器坐標的初始近似值x2ref得到最優估值x2lsq。解算出Δx2lsq後，對式(39)從下至上依次回代，即可按順序解算出局部參數向量按照式(20)加到局部參數初始近似值x1ref(n),x1ref(n-1),…,x1ref(2),x1ref(1)，即可得各個弧段局部參數對應的最優估值x1lsq(n),x1lsq(n-1),…,x1lsq(2),x1lsq(1)。

由於上述過程基於將非線性的方程線性化，為更準確的解算參數，數學上通常將線性化後的非線性方程使用迭代法求解。參見圖4，實施例提供的具體流程闡述如下：

第一，對於第一個弧段，按照①～⑥形成如式(36)所示的法方程。

第二，對於第2～N個弧段，按照①～⑥與第一個弧段按照上一步驟形成的法方程一起形成如式(37)所示的法方程。

第三，按照式(37)和式(38)融合多弧段法方程，形成如式(39)所示的形式；即生成弧段(1)～(N)對中繼星初軌、力模型參數(局部參數)的偏導數，生成對著陸器坐標(全局參數)的偏導數，可生成弧段(1)～(N)的法方程，開始融合弧段(1)～(N)的法方程進行著陸器坐標(全局參數)解算。

第四，解算出全局參數向量的第一次的改正值Δx2lsq，按照式(20)加到遠月面著陸器坐標的初始近似值x2ref得到第一次的最優估值x2lsq。

第五，將當前的最優估值x2lsq重新作為初始近似值x2ref，並按照①～⑥的步驟更新第三步中的法方程中的矩陣形成新的多弧段融合的法方程。其中，i＝N,N-1,…1，表示第i個弧段。第一次執行第五步時，當前的最優估值即採用第四步中第一次得到的全局參數的最優估值x2lsq。

第六，根據新的法方程解算出新的全局參數向量的改正值Δx2lsq，按照式(20)加到遠月面著陸器坐標的初始近似值x2ref得到新的最優估值x2lsq。

第七，重複第五步和第六步，直至當次迭代和上一次迭代得到的Δx2lsq之差的絕對值小於預設的相應限差δ2停止迭代，得到最終的全局參數的最優估值x2lsq。具體實施時，本領域技術人員可自行根據精度需要設置限差δ2，可將流程設計為判斷是否滿足著陸器坐標收斂條件，是則完成著陸器坐標(全局參數)的最後一次迭代，獲取著陸器坐標(全局參數)精密坐標，否則返回進行全局參數迭代。

第八，解算出最新的Δx2lsq後，按照從下到上的次序回代到由以上步驟形成的最新的多弧段融合的法方程中，形式如式(39)所示，依次解算出第一次的局部參數的改正值按照式(20)加到局部參數初始近似值x1ref(n),x1ref(n-1),…,x1ref(2),x1ref(1)，即可得各個弧段局部參數對應的第一次的最優估值x1lsq(n),x1lsq(n-1),…,x1lsq(2),x1lsq(1)。

第九，將第一次得到的局部參數的最優估值x1lsq(i)重新作為初始近似值x1ref(i)，按照①～⑥的步驟更新法方程中的矩陣形成新的多弧段融合的法方程。其中，i＝N,N-1,…1，表示第i個弧段。

第十，根據新的法方程解算出新的局部參數向量的改正值按照式(20)加到各個弧段局部參數的初始近似值x1ref(i)得到新的最優估值x1lsq(i)，其中，i＝N,N-1,…1，表示第i個弧段。

第十一，重複第九和第十步，直至當次迭代和上次迭代得到的之差的絕對值小於預設的相應限差δ1停止迭代，得到最終局部參數的最優估值x1lsq(i)，其中，i＝N,N-1,…1，表示第i個弧段。具體實施時，本領域技術人員可自行根據精度需要設置限差δ1，可將流程設計為判斷是否滿足局部參數收斂條件，是則完成中繼星初軌、力模型參數(局部參數)的最後一次迭代，獲取中繼星初軌、力模型參數估值，否則返回進行局部參數迭代。

至此，根據以上流程，得到最終穩定的中繼星精密軌道和遠月面著陸器的精密坐標。具體實施時，可採用計算機軟體技術實現自動流程運行。

以上所述，僅為本發明較佳的具體實施方式，本發明的保護範圍不限於此，任何熟悉本技術領域的技術人員在本發明披露的技術範圍內，可顯而易見地得到的技術方案的簡單變化或等效替換均落入本發明的保護範圍內。