基於空間相鄰波高數據相關性的海浪波長測量方法與流程
2023-06-02 19:03:19
本發明涉及海洋海浪波長測量技術領域,具體地說,是涉及一種基於空間相鄰波高數據相關性的波長測量方法。
背景技術:
最常見的且與人類活動關係最密切建設有著十分重要的指導作用。同時,研究海浪對全球大洋的海氣相互作用及氣候變化也有著非常重要的意義。海浪的主要要素包括有效波高、波長、波周期等等,其中有效波高及波周期可以通過波高計測量得到(文聖常,1984),比較簡便,而波長的測量則較為複雜,這也成為眾多學者研究的焦點,這一工作在海洋科學研究中已經成為一項極為關鍵的技術。
目前常用的波長測量方法分為以下幾種:一.根據有限水深中的波浪頻散關係,通過波周期計算得到;二.根據圖像直接得到;三.根據不同波高計之間的相關關係計算得到。
李孟國(2002)介紹了用波浪彌散關係確定淺水波長的方法,討論了水深、水流、波浪振幅對波長的影響。根據波浪譜間接計算波長的理論比較成熟,但需要假定波浪為線性且受水深等因素的影響。因此,為了得到更精確、更可靠的數據,直接測量方法有著不可替代的作用。
隨著科技發展,衛星數據的增多,許多中外學者開始研究如何根據雷達或衛星圖片分析大範圍甚至全球波長分布。使用衛星觀測對於研究全球大洋波長分布有著十分重要的意義,具體到小尺度研究,卻存在測量精度比較低及無法實時監測的缺點。
馮越(2016)提出了利用兩個海浪測量杆,測量通過兩個測量杆之間波浪的傳播時間計算波速與波長的方法。這些方法能夠方便且有效的測量波長,在實際應用中還存在一些需要解決的問題,若兩個波高計之間距離過長,由于波浪狀況一直在變化,很難找到對應的波浪確定時間;若波高計之間距離過短,解析度太低導致結果誤差較大,實際海面的波浪是在不停變化,根據兩個波高計測量波長需要解決準確測量通過兩個波高計之間的時間的問題。
技術實現要素:
本發明為了解決現有通過波高計測量海浪波長的方式存在測量精度低或者解析度低的技術問題,提出了一種基於空間相鄰波高數據相關性的海浪波長測量方法,可以解決上述問題。
為了解決上述技術問題,本發明採用以下技術方案予以實現:
一種基於空間相鄰波高數據相關性的海浪波長測量方法,包括以下步驟:
(1)、設置空間相鄰的兩個波高採集裝置,用於同時採集兩組波高時間序列數據,若兩個波高計不是同時啟動,記錄兩個波高採集裝置啟動的時間差δt1,分別將該兩組波高時間序列數據進行預處理,兩個波高採集裝置的採樣周期為t1;
(2)、分別對所述兩組波高時間序列數據進行傅立葉變換,將各組波高時間序列數據從時域轉換至頻域,得到一系列不同頻率的正弦函數的疊加,為波高時間序列數據在頻域的原始解析式;
(3)、原始解析式中將各頻率的正弦函數按其振幅從大到小排序,選取能量之和與總能量的比值大於m的前m個正弦函數,該前m個正弦函數之和即為波高時間序列數據在頻域的新解析式,其中,0<m<1,m為正整數;
(4)、將所述新解析式與所述原始解析式進行比較,判斷標準差是否小於n,若是,則將所述新解析式進行重採樣,否則,返回步驟(3),增加m的值,直至滿足標準差小於n,其中,0<n<0.05
(5)、將新解析式在時域進行插值,計算出在時域插值後的波高數據,擬合波高數據時,每一組波高時間序列數據對應一組擬合波高數據;
(6)、將兩組擬合波高數據做延遲相關,找到兩組擬合波高數據相關度最高的延遲時間△t,為同一海浪依次通過所述空間相鄰的兩個波高採集裝置的時間;
(7)、根據延遲時間△t計算依次通過所述空間相鄰的兩個波高採集裝置的海浪的波長λ。
進一步的,步驟(3)中,按振幅從大到小排序後的原始解析式的表達方程為:
h=a0+a1sin(b1t+c1)+…+ansin(bnt+cn)
其中a0,a1…an代表振幅,b0,b1…bn代表頻率,c0,c1…cn為相位,n為波高時間序列數據的長度,為正整數。
進一步的,步驟(3)中,滿足其中,m<n;
步驟(3)中新解析式為:hm=a0+a1sin(b1t+c1)+…+amsin(bmt+cm)。
進一步的,步驟(5)中將新解析式在時域進行插值的方法為:將新解析式中時間步長設定為採樣周期的k倍,其中,0<k<0.05,擬合波高數據的數據量為其所對應波高時間序列數據的數據量的1/k倍。
進一步的,步驟(2)中分別對所述兩組波高時間序列數據進行傅立葉變換後還包括計算其頻譜譜峰周期tp的步驟。
進一步的,步驟(7)中,波長λ的計算方法為:
c=l/(δt+δt1)
λ=c·tp
其中,c為波動相速度,l為兩個波高採集裝置之間距離。
進一步的,所述兩個波高採集裝置之間的距離為5cm~20cm。
進一步的,所述兩個波高採集裝置為波高計。
與現有技術相比,本發明的優點和積極效果是:本發明的基於空間相鄰波高數據相關性的海浪波長測量方法,通過縮短兩個波高計之間距離,提高測量準確度,同時通過只保留能量之和佔總能量一定比例的波浪頻率,並進行插值,一方面減小了數據計算量,另外一方面可以提高採樣間隔的解析度。
結合附圖閱讀本發明實施方式的詳細描述後,本發明的其他特點和優點將變得更加清楚。
附圖說明
為了更清楚地說明本發明實施例或現有技術中的技術方案,下面將對實施例或現有技術描述中所需要使用的附圖作簡單地介紹,顯而易見地,下面描述中的附圖僅僅是本發明的一些實施例,對於本領域普通技術人員來講,在不付出創造性勞動的前提下,還可以根據這些附圖獲得其他的附圖。
圖1是本發明所提出的海浪波長測量方法的一種實施例流程圖;
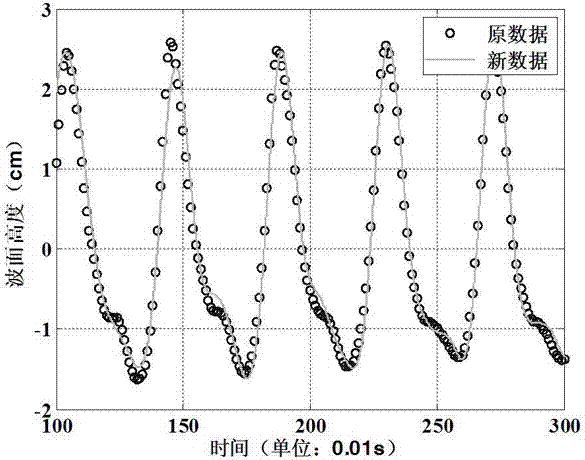
圖2是本發明所提出的海浪波長測量方法的一種實施例中插值前後波形對比圖。
具體實施方式
下面將結合本發明實施例中的附圖,對本發明實施例中的技術方案進行清楚、完整地描述,顯然,所描述的實施例僅僅是本發明一部分實施例,而不是全部的實施例。基於本發明中的實施例,本領域普通技術人員在沒有做出創造性勞動前提下所獲得的所有其他實施例,都屬於本發明保護的範圍。
實施例一,本實施例提出了一種基於空間相鄰波高數據相關性的海浪波長測量方法,如圖1所示,包括以下步驟:
s1、設置空間相鄰的兩個波高採集裝置,用於同時採集兩組波高時間序列數據,若兩個波高計不是同時啟動,記錄兩個波高採集裝置啟動的時間差δt1,分別將該兩組波高時間序列數據進行預處理,兩個波高採集裝置的採樣周期為t1;
在實際測量過程中,一般通過向海洋裡投放檢測浮標的方式,浮標上搭載有波高採集裝置,進行波高的測量,為了保證兩個波高採集裝置之間距離恆定,同一浮標上可以搭載有兩個或者以上波高採集裝置,在選取數據時,選擇其中的兩組數據進行處理,海浪在傳遞過程中,依次經過兩個相鄰的波高採集裝置,波高採集裝置周期性採集其當前位置的波高並記錄保存,實時上傳至地面站或者定期上傳,由地面進行數據處理。本申請中,兩個波高採集裝置之間的距離為5cm~20cm,距離較近,利於提高測量的準確度。
其中,波高採集裝置可以採用波高計實現。
s2、分別對所述兩組波高時間序列數據進行傅立葉變換,將各組波高時間序列數據從時域轉換至頻域,得到一系列不同頻率的正弦函數的疊加,為波高時間序列數據在頻域的原始解析式;海浪在頻域實際由若干頻率的正弦函數疊加而成,且每個正弦函數根據能量大小都有各自的振幅,振幅越大,相應的能量越大,通過將波高採集裝置所採集的離散的波高時間序列數據轉換至頻域,便於從中選取能量最集中的若干頻率的波形。
s3、原始解析式中將各頻率的正弦函數按其振幅從大到小排序,選取能量之和與總能量的比值大於m的前m個正弦函數,該前m個正弦函數之和即為波高時間序列數據在頻域的新解析式,其中,0<m<1,m為正整數;通過濾除掉能量佔比較小頻率的波形,而往往能量佔比較小的頻率的正弦波數量極其龐大,因此,將其濾除掉後可以極大的減小計算量。
s4、將所述新解析式與所述原始解析式進行比較,判斷標準差是否小於n,若是,則將所述新解析式進行重採樣,否則,返回步驟(3),增加m的值,直至滿足標準差小於n,其中,0<n<0.05;得到新解析式後,與原始解析式對比,若誤差較大,需選取更多的組成波疊加,直到標準差控制在n以內。通過將新解析式與所述原始解析式之間的標準差限定在一定範圍內,保證保留下來數據的波形與原波形不會產生大失真,例如,n可以取值5%。
s5、將新解析式在時域進行插值,計算出在時域插值後的波高數據,擬合波高數據時,每一組波高時間序列數據對應一組擬合波高數據;由于波高採集裝置的採集頻率有限,因此波高時間序列數據的數據量也有限,考慮到波浪狀況一直在變化,數據量小導致計算波長時解析度太低,通過插值的方式提高數據解析度。
s6、將兩組擬合波高數據做延遲相關,找到兩組擬合波高數據相關度最高的延遲時間△t,為同一海浪依次通過所述空間相鄰的兩個波高採集裝置的時間;由前面記載可知,兩個波高採集裝置周期採集其位置處當前的波高數據,而海浪從一個波高採集裝置傳遞至另一個波高採集裝置具有一定的時間延遲,因此,為了找到海浪從一個波高採集裝置傳遞至另一個波高採集裝置的時間延遲,需要根據波形特徵將兩組擬合波高數據的波形對齊,也即,本申請中採用延遲相關的方式,其中一組擬合波高數據不動,另外一組擬合波高數據在時間上做延遲,選取的延遲時間分別為△t1、△t2…,只選取其延遲後的時間段的擬合波高數據,然後與未做延遲的擬合波高數據進行相關計算,找到相關值最大的一組延遲擬合波高數據,其所對應的延遲時間記為△t。
s7、根據延遲時間△t計算依次通過所述空間相鄰的兩個波高採集裝置的海浪的波長λ。
本發明的基於空間相鄰波高數據相關性的海浪波長測量方法,通過縮短兩個波高計之間距離,提高測量準確度,同時通過只保留能量之和佔總能量一定比例的波浪頻率,並進行插值,一方面減小了數據計算量,另外一方面可以提高採樣間隔的解析度。
作為一個優選的實施例,步驟s3中,按振幅從大到小排序後的原始解析式的表達方程為:
h=a0+a1sin(b1t+c1)+…+ansin(bnt+cn)
其中a0,a1…an代表振幅,b0,b1…bn代表頻率,c0,c1…cn為相位,n為波高時間序列數據的長度,為正整數。
步驟s3中,滿足其中,m<n;由于波浪能量與振幅平方成正比,因此,為波動的總能量,將所有分解出的組成波按振幅排序。通常情況下,波浪的大部分能量主要集中在幾個譜峰周圍,經過對所有波浪情況的計算,振幅前10%的波浪的能量約為波浪總能量的95%,因此本申請中可以選取總能量95%的組成波疊加能夠較完整的保留波浪信息並減少計算量,也即,m取值為95%。
因此,步驟s3中新解析式為:hm=a0+a1sin(b1t+c1)+…+amsin(bmt+cm)。
步驟s5中將新解析式在時域進行插值的方法為:將新解析式中時間步長設定為採樣周期的k倍,其中,0<k<0.05,擬合波高數據的數據量為其所對應波高時間序列數據的數據量的1/k倍。
例如,將新解析式中時間步長選取為採樣周期的1%,得到的數據量為原數據量的100倍,相應可提高100倍解析度。通過該方法得到的擬合波高數據與原波高時間序列數據的對比如圖2所示。由圖2可知,在解析度提高100倍時,該方法得到的數據與原波浪數據基本吻合,不會因為解析度提高產生偏差。擬合數據與原數據的偏差是由於只選取95%的能量,因此採樣間隔只提高100倍,減少誤差的產生。若選取更多的能量疊加,可以在提高更多解析度時得到更精確的結果,但計算量會增加。同時,由於原始數據可能存在由於儀器產生的誤差或其他隨機誤差,過多的提高解析度得到的結果並不一定準確。兼顧計算量、準確性以及更多的提高解析度後,提高100倍解析度為較好的選擇。
步驟s2中分別對所述兩組波高時間序列數據進行傅立葉變換後還包括計算其頻譜譜峰周期tp的步驟。
步驟s7中,波長λ的計算方法為:
c=l/(δt+δt1)
λ=c·tp
其中,c為波動相速度,l為兩個波高採集裝置之間距離。
為了保證兩個波高採集裝置的同步性,去除因為兩個波高計不同時啟動產生的誤差,計算波長λ時應當考慮到兩個波高採集裝置啟動的時間差。當兩個波高採集裝置同時啟動時,δt1=0。
當然,上述說明並非是對本發明的限制,本發明也並不僅限於上述舉例,本技術領域的普通技術人員在本發明的實質範圍內所做出的變化、改型、添加或替換,也應屬於本發明的保護範圍。
