隨機數生成裝置、隨機數生成方法以及程序與流程
2023-09-21 10:34:10
本發明涉及隨機數生成技術,特別涉及生成屬於規定的集合的隨機數的技術。
背景技術:
存在生成n個隨機比特,對與將該n個隨機比特設為各位的值的二進位數表示值對應的十進位數表示值a和p-1進行大小判定,若a>p-1則重新進行處理,否則採用a作為隨機數的隨機數生成方法(例如參照非專利文獻1)。若將p設為素數,則可以生成素域上的隨機數。
[現有技術文獻]
[非專利文獻]
[非專利文獻1]:ヨハネスブーフマン、「暗號理論入門―暗號アルゴリズム、署名と認証、その數學的基礎」、シュプリンガー·フェアラーク東京、2001年7月、p114.
技術實現要素:
發明要解決的課題
在上述的方法中,在對於n以二進位數表示p時的要素數小時,隨機數的生成概率極度下降,導致隨機數的生成速度下降。
本發明的課題在於,高速地生成屬於規定的集合的隨機數。
用於解決課題的方案
得到將以二進位數表示的隨機數的各位的值包含於要素的第一列,得到該第一列和將以二進位數表示的單個或者多個梅森數的各位的值以及零值包含於要素的第二列之間的要素單位的邏輯與運算結果、即第三列。
發明效果
由此,能夠高速地生成屬於規定的集合的隨機數。
附圖說明
圖1是例示了實施方式的隨機數生成裝置的功能結構的框圖。
圖2a是例示了實施方式的隨機數生成方法的流程圖。圖2b是例示了等號判定處理的流程圖。
圖3a~圖3c是例示了實施方式的第一~三列的圖。
具體實施方式
以下,說明本發明的實施方式。
[概要]
在實施方式中,如以下那樣生成屬於規定的集合的隨機數。首先,得到將以二進位數表示的隨機數(二進位隨機數)的各位的值包含於要素的「第一列」(隨機數獲取步驟)。該隨機數可以是均勻隨機數,也可以不是均勻隨機數。再者,「隨機數」的概念包含真隨機數及偽隨機數。隨機數可以預先生成,也可以在得到「第一列」時生成。「第一列」可以僅將以二進位數表示的隨機數的各位的值作為要素,也可以進一步包含除此以外的要素。接著,得到「第一列」和「第二列」的要素單位的邏輯與運算結果(各要素的與(and)運算結果,例如比特與運算結果)、即「第三列」(邏輯與運算步驟)。其中,「第二列」是將以二進位數表示的單個或者多個梅森數pi(其中,i=0、…、n-1,n是1以上的整數)的各位的值以及零值包含於要素的列。「第二列」的要素數例如與「第一列」的要素數相同。「第二列」可以僅將梅森數pi的各位的值以及零值作為要素,也可以進一步包含除此以外的要素(例如固定值、屬性信息等)。梅森數pi是滿足2n(i)-1的整數,以二進位數表示的梅森數pi是由n(i)個1構成的列1…1。其中,n(i)是特定的正整數。pi的一個例子是梅森素數,例如在n(i)=2、3、5、7、13、17、19、31、61等時pi成為梅森素數。「第三列」是用「第二列」對「第一列」進行掩蓋後的列,是包含以二進位數表示的位數為n(i)的隨機數ti的列。這樣的隨機數ti能夠處理為以梅森數pi為模的剩餘環(剩餘類)上的隨機數。特別地,若pi是梅森素數,則隨機數ti能夠處理為以梅森素數pi為模的剩餘域(素域)上的隨機數。在以pi為模的剩餘環上,pi=2n(i)-1和0是相同的值(2n(i)-1mod(2n(i)-1)=0),「第三列」所包含的n個隨機數ti(其中,i=0、…、n-1)「必定」可以處理為以pi為模的剩餘環上的隨機數。因此,與隨機數的生成概率因環境而下降的現有技術相比,能夠高速地生成剩餘環上的隨機數。
但是,在以pi為模的剩餘環中pi和0被處理為相同的值(0是pi的等價類),所以隨機數ti不限於成為均勻隨機數。即,在「第一列」所表示的隨機數是均勻隨機數的情況下,ti成為0、1、…、pi的概率分別為1/2n(i),ti成為pi或者0的概率為1/2n(i)-1。因此,在上述剩餘環上,0的生成概率(換言之,pi的生成概率)為1/2n(i)-1,其他隨機數的生成概率為1/2n(i)。為了得到剩餘環上的均勻隨機數,在成為了ti=pi的情況下,廢棄所生成的隨機數,並重新進行隨機數獲取步驟及邏輯與運算步驟即可。換言之,「第一列」包含「第一子列」,「第二列」所包含的「第二子列」表示任意的梅森數pi,「第三列」包含「第一子列」和「第二子列」的要素單位的邏輯與運算結果、即「第三子列」,在「第二子列」和「第三子列」一致的情況下再次執行隨機數獲取步驟及邏輯與運算步驟的處理即可。在上述結構中,成為ti=pi的概率(「第二子列」和「第三子列」一致的概率)也是1/2n(i)-1左右,能夠高速地生成剩餘環上的均勻隨機數。
或者,也可以在成為ti=0的情況下重新進行隨機數獲取步驟及邏輯與運算步驟。換言之,也可以在「第三子列」的要素由零構成的情況(「第三子列」為零向量的情況)下再次執行隨機數獲取步驟及邏輯與運算步驟的處理。由此,也能夠高速地生成剩餘環上的均勻隨機數。
此外,在將n設為2以上的整數、將「第二列」設為將以二進位數表示的多個梅森數pi的各位的值以及零值包含於要素的列的情況下,能夠通過並行處理來生成多個剩餘環上的隨機數,能夠更高速地生成隨機數。以二進位數表示的梅森數pi的位數(比特長度)n(i)可以彼此相同,也可以不相同。
在通過這樣的並行處理來生成剩餘環上的均勻隨機數的情況下,也可以是,(1)通過集中等號判定,對i=0、…、n-1集中地進行是否成為ti=pi的判定,(2)通過這些等號判定結果xi(其中,i=0、…、n-1)的或運算或者與運算,對任意的i得到表示是否成為ti=pi的聚合判定結果x,(3)在聚合判定結果x對任意的i表示成為ti=pi的情況下重新進行隨機數獲取步驟及邏輯與運算步驟。換言之,也可以是,(1)通過集中等號判定來得到表示多個「第二子列」中的每個和多個「第三子列」中的每個是否一致的多個等號判定結果xi(其中,i=0、…、n-1)的每一個,(2)通過多個等號判定結果xi的或運算或者與運算來得到表示任意的「第二子列」和「第三子列」是否一致的聚合判定結果x,(3)在聚合判定結果x表示任意的「第二子列」和「第三子列」一致的情況下,再次執行隨機數獲取步驟及邏輯與運算步驟的處理。其中,「第一列」包含多個「第一子列」,「第二列」所包含的多個「第二子列」的每一個表示多個梅森數pi的各位的值,「第三列」包含多個「第三子列」,多個「第三子列」的每個是多個「第一子列」中的每個和多個「第二子列」中的每個的要素單位的邏輯與運算結果ti。這裡,集中等號判定、或運算、與運算的運算量較小。此外,如上述,成為ti=pi的概率是1/2n(i)-1左右,對任意的i,成為ti=pi的可能性小。因此,能夠更高速地生成剩餘環上的均勻隨機數。
或者,也可以是,(4)通過集中等號判定,對i=0、…、n-1集中地進行是否成為ti=0的判定,(5)通過這些等號判定結果xi(其中,i=0、…、n-1)的或運算或者與運算,對任意的i得到表示是否成為ti=0的聚合判定結果x,(6)在聚合判定結果x對任意的i表示成為ti=0的情況下重新進行隨機數獲取步驟及邏輯與運算步驟。換言之,也可以是,(4)通過集中等號判定來得到表示多個「第三子列」的每個的要素是否由零構成的多個等號判定結果xi(其中,i=0、…、n-1)的每一個,(5)通過多個等號判定結果xi的或運算或者與運算來得到表示任意的「第三子列」的要素是否由零構成的聚合判定結果x,(6)在聚合判定結果x表示任意的「第三子列」的要素由零構成的情況下,再次執行隨機數獲取步驟及邏輯與運算步驟的處理。在該情況下,也能夠高速地生成剩餘環上的均勻隨機數。
[第一實施方式]
接著,說明第一實施方式。在本方式中,說明pi為梅森素數的情況。
<結構>
如圖1所例示的,本方式的隨機數生成裝置1具有二進位隨機數生成單元11、存儲單元12、輸入單元13、掩碼生成單元14、隨機數獲取單元15、邏輯與運算單元16、以及輸出單元18。隨機數生成裝置1例如是通過由包括cpu(centralprocessingunit,中央處理單元)等的處理器(硬體/處理器)、ram(random-accessmemory,隨機存取存儲器)/rom(read-onlymemory,只讀存儲器)等的存儲器等的通用或者專用的計算機執行規定的程序而構成的裝置。該計算機可以包括1個處理器、存儲器,也可以包括多個處理器、存儲器。該程序可以安裝於計算機,也可以預先記錄於rom等。此外,也可以不利用如cpu那樣通過讀入程序而實現功能結構的電路(circuitry),而利用不用程序就實現處理功能的電路來構成一部分或者全部的處理單元。此外,構成1個裝置的電路也可以包含多個cpu。
<處理>
在本方式中,將「第一列」、「第二列」、「第三列」處理為分別由l個要素構成的向量,假設隨機數生成裝置1是以l比特精度進行運算的隨機數生成裝置。此外,l是比以二進位數表示的梅森素數p0、…、pn-1的合計要素數n(0)+…+n(n-1)更大的正整數。l可以是常數,也可以根據被輸入的梅森素數p0、…、pn-1來確定。在所假定的梅森素數p0、…、pn-1的大小被預先確定的情況下,能夠將l設為常數。
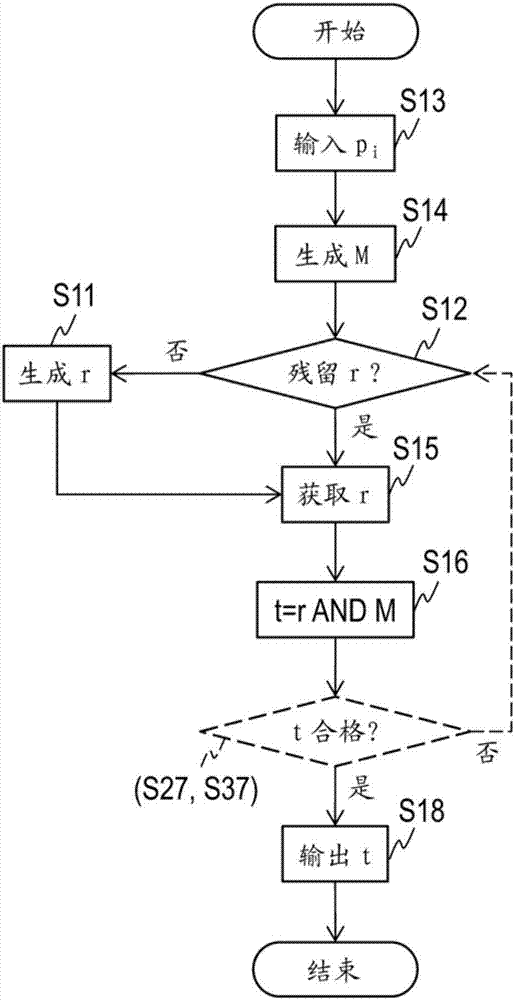
如圖2a所例示的,首先,對梅森素數p0、…、pn-1進行確定的信息被輸入到輸入單元13。該信息的例子是梅森素數p0、…、pn-1本身或n(0)、…、n(n-1)等。對梅森素數p0、…、pn-1進行確定的信息被發送到掩碼生成單元14(步驟s13)。
掩碼生成單元14得到由l個要素構成的向量m∈{0,1}l(第二列),並輸出,其中,該l個要素將以二進位數表示的梅森素數p0、…、pn-1的各位的值以及零值包含於要素。在圖3a~3c中示出向量m的具體例。圖3a的例子是n(0)=…=n(n-1)=7的例子。就該例的向量m而言,起始的z個(其中,z=l-(n(0)+…+n(n-1)))的要素為零,其餘的要素全部為1。換言之,在由起始的z個0構成的子列zero之後,配置有以二進位數表示的梅森素數pn-1、…、p0。圖3b的例子也是n(0)=…=n(n-1)=7的例子。但是,在該例中,在1個0的要素zero之後配置有以二進位數表示的1個梅森素數pi(其中,i=n-1、…、0),交替地配置有0和以二進位數表示的梅森素數pi。在圖3c中,在由起始的z個0構成的子列zero之後,配置有由二進位數表示的梅森素數pn-1、…、p0。但是,梅森素數pn-1、…、p0並不全都相同。此外,在圖3b的例子中,梅森素數pn-1、…、p0也可以不全都相同。所生成的向量m被發送到邏輯與運算單元16(步驟s14)。
隨機數獲取單元15判定存儲單元12中是否殘留有由l個要素構成的l比特的二進位隨機數向量r∈{0,1}l(第一列)(步驟s12)。在殘留有二進位隨機數向量r的情況下,隨機數獲取單元15從存儲單元12讀出二進位隨機數向量r,並輸出(步驟s15)。被讀出的二進位隨機數向量r被從存儲單元12中刪除。另一方面,在未殘留二進位隨機數向量r的情況下,二進位隨機數生成單元11生成l比特的二進位隨機數向量r∈{0,1}l,存儲到存儲單元12中,隨機數獲取單元15從存儲單元12讀出二進位隨機數向量r,並輸出(步驟s15)。再者,為了處理的高速化,期望二進位隨機數生成單元11通過並行處理來生成多個二進位隨機數向量r,存儲到存儲單元12中。所輸出的二進位隨機數向量r被發送到邏輯與運算單元16。
邏輯與運算單元16進行二進位隨機數向量r和向量m的要素單位的邏輯與運算(比特與運算),得到其運算結果、即向量t∈{0,1}l(第三列),並輸出。在向量m的第j要素(其中,j=0、…、l-1)為零的情況下,向量t的第j要素成為零,在向量m的第j要素為1的情況下,向量t的第j要素成為二進位隨機數向量r的第j要素。即,向量t是用向量m對二進位隨機數向量r進行掩蓋得到的向量。將與向量m所包含的以二進位數表示的梅森素數pi的要素列(子列)對應的向量t的要素列表示為子列ti。例如,在以二進位數表示的梅森素數pi是向量m的從第j1要素起至第j2要素為止的要素列的情況下,子列ti是向量t的從第j1要素起至第j2要素為止的要素列。例如,在圖3a的例子的情況下,二進位隨機數向量r的起始的z個要素是由(rn,z-1,···,rn,0)∈{0,1}z構成的子列rn。其中,向量m的起始的z個要素全部為零,所以向量t的起始的z個要素也全部為零。之後的向量m的要素全部為1,所以向量t的之後的子列tn-1、…、t0(其中,ti是由ti,6、···、ti,0∈{0,1}7構成的子列)是二進位隨機數向量r的子列rn-1、…、r0(其中,ri是由ri,6、···、ri,0∈{0,1}7構成的子列)。例如,在圖3b的例子的情況下,二進位隨機數向量r由子列rn-1、…、r0(其中,ri是由ri,7、···、ri,0∈{0,1}7構成的子列)構成。向量m具有n個由0和1111111構成的子列01111111,所以向量t的子列tn-1、…、t0(其中,ti是由ti,6、···、ti,0∈{0,1}7構成的子列)是二進位隨機數向量r的子列rn-1、…、r0(其中,ri是由ri,6、···、ri,0∈{0,1}7構成的子列)。例如,在圖3c的例子的情況下,向量m的起始的z個要素全部為零,其餘的要素全部為1。因此,向量t的起始的z個要素全部為零,之後的子列tn-1、…、t0是二進位隨機數向量r的子列rn-1、…、r0。所得到的向量t被發送到輸出單元18(步驟s16)。
輸出單元18可以將向量t直接輸出,也可以僅輸出向量t所包含的子列tn-1、…、t0。子列ti(其中,i=0、…、n-1)分別被處理為以梅森素數pi為模的剩餘域(素域)上的隨機數(步驟s18)。在進一步需要素域上的隨機數的情況下,反覆進行從步驟s13至s18的處理或者s11~s18的處理即可。
<本方式的特徵>
在像以往那樣通過二進位隨機數向量r所表示的值和素數p的大小判定來生成素域上的隨機數的情況下,若相對於二進位隨機數向量r的要素數l,以二進位數表示p時的要素數小,則該素域上的隨機數的生成概率極度下降,導致隨機數的生成速度下降。例如,在二進位隨機數向量r表示均勻隨機數,以二進位數表示p時的要素數為l-1的情況下,若p是梅森素數,則該素域上的隨機數的生成概率成為50%,若p是除梅森素數以外的素數,則生成概率小於50%。在進行並行處理的情況下,該生成概率進一步下降。例如,在成功概率為50%左右時,若試圖並行地進行1000個素數生成,則失敗概率成為99.9%左右,幾乎不會成功,性能極度下降。
與此相對,在本方式中,能夠可靠地生成素域上的隨機數,所以能夠高速地生成素數域上的隨機數。進一步,即使並行地集中進行每個要素的邏輯與運算(n≥2)來進行隨機數生成,成功概率也不會下降,所以能夠通過這樣的並行處理來更高速地生成素域上的隨機數。此外,許多計算機能夠並行地高速地處理比特與運算(每個要素的邏輯與運算),能夠高效地實現本方式的方法。進一步,能夠由l比特的寄存器來執行本方式的比特與運算,與以往那樣進行大小比較的情況相比能夠削減存儲容量。
[第二實施方式]
本方式中生成素域上的均勻隨機數。以下,以與到此為止說明過的事項的不同點為中心進行說明,對已經說明過的事項,引用與之相同的參照編號而省略說明。
<結構>
如圖1所例示的,本方式的隨機數生成裝置2具有二進位隨機數生成單元11、存儲單元12、輸入單元13、掩碼生成單元14、隨機數獲取單元15、邏輯與運算單元16、判定單元27、以及輸出單元18。隨機數生成裝置2例如可以通過將規定的程序讀入上述的計算機來構成,也可以僅由硬體來構成至少一部分的要素。
<處理>
步驟s11~s16的處理與第一實施方式相同。但是,在第二實施方式中,輸入到輸入單元13的梅森素數pi以及在步驟s16中得到的向量t被輸入到判定單元27。判定單元27判定向量t所包含的任意的子列ti和梅森素數pi(其中,i=0、…、n-1)是否一致(等號判定)(步驟s27)。在對任意的i=0、…、n-1,ti=pi的情況下,判定單元27廢棄向量t(t不合格),將處理返回到步驟s12。另一方面,在對全部的i=0、…、n-1,ti≠pi的情況下,向量t被發送到輸出單元18(t合格)。以後與第一實施方式相同。
再者,步驟s27的等號判定也可以對每個i獨立地進行,但是也可以如圖2b所例示的那樣集中處理。在圖2b的例子中,判定單元27的集中等號判定單元對全部的i=0、…、n-1集中地進行是否ti=pi的等號判定(集中等號判定),得到等號判定結果xi的列。其中,在ti=pi的情況下xi=2k-1,在ti≠pi的情況下xi=0。再者,k為正整數,滿足0<k×n≤l(步驟s271)。接著,判定單元27的聚合運算單元進行等號判定結果xi(其中,i=0、…、n-1)的聚合或運算(or運算),得到其運算結果、即聚合判定結果x。其中,在任意的等號判定結果xi(其中,i=0、…、n-1)為2k-1的情況(非0的情況)下x=2k』-1,在全部的等號判定結果xi(其中,i=0、…、n-1)為0的情況下x=0。再者,k』為正整數,滿足0<k』≤l。可以是k=k』,也可以是k≠k』(步驟s272)。然後,判定單元27的聚合判定單元判定是否x=0(步驟s273)。這裡,若x=2k-1則聚合判定單元廢棄向量t(t不合格)(步驟s274),將處理返回到步驟s12。另一方面,若x=0則聚合判定單元將向量t發送到輸出單元18(t合格)(步驟s275)。
另外,也可以是,集中等號判定單元在ti=pi的情況下設為xi=0,在ti≠pi的情況下設為xi=2k-1,聚合運算單元進行xi(其中,i=0、…、n-1)的聚合與運算(and運算),得到其運算結果、即聚合判定結果x。其中,在任意的等號判定結果xi(其中,i=0、…、n-1)為0的情況下x=0,在全部的等號判定結果xi(其中,i=0、…、n-1)為2k-1的情況下x=2k』-1。在該情況下,若x=0則聚合判定單元廢棄向量t(t不合格),將處理返回到步驟s12。另一方面,若x=2k-1則聚合判定單元將向量t發送到輸出單元18(t合格)。
<本方式的特徵>
如前述,若二進位隨機數向量r表示均勻隨機數,則子列ti分別成為以梅森素數pi為模的剩餘域(素域)上的均勻隨機數。成為ti=pi的概率是1/2n(i)-1左右,不論l的大小如何,成功概率均高。本方式也大致可靠地成功地生成隨機數,所以即使並行地集中進行子列ti(其中,i=0、…、n-1)的等號判定,成功概率也幾乎不會下降,在步驟s27中成為不合格的概率低。例如,在p=261-1(即n(i)=61)時,1000個並行的集中生成失敗的概率為1/251,充分低,重新進行的開銷(overhead)極小。因此,若如上述那樣集中處理步驟s27的等號判定,則能夠更高速地得到素域上的均勻隨機數。即,上述的集中等號判定、聚合或運算(或者聚合與運算)的運算成本低。例如在l=256的情況下,許多計算機能夠用1個時鐘來處理這些處理。此外,當前的許多計算機具有分支預測功能,在進行分支計算前,實績多的計算機的分支先開始處理,所以若重新進行的概率低,則條件分支實際上成為0時鐘。此外,掩碼即向量m∈{0,1}l所包含的梅森素數p0、…、pn-1與等號判定基準一致,所以可以將為了掩碼處理而預先存儲了向量m的寄存器還用於等號判定處理,能夠用少的寄存器來實現這些處理。此外,等號判定與現有方式所使用的大小比較相比還具有效率高的優點(對比特數n,大小比較為電路規模o(n)/深度o(n)或者電路規模o(nlogn)/深度o(logn),與此相對,等號判定為電路規模o(n)/深度o(logn))。
[第三實施方式]
本方式也生成素域上的均勻隨機數。以下,以與到此為止說明過的事項的不同點為中心進行說明,對已經說明過的事項,引用與之相同的參照編號而省略說明。
<結構>
如圖1所例示的,本方式的隨機數生成裝置3具有二進位隨機數生成單元11、存儲單元12、輸入單元13、掩碼生成單元14、隨機數獲取單元15、邏輯與運算單元16、判定單元37、以及輸出單元18。隨機數生成裝置3例如可以通過將規定的程序讀入上述的計算機來構成,也可以僅由硬體來構成至少一部分的要素。
<處理>
步驟s11~s16的處理與第一實施方式相同。但是,在第三實施方式中,在步驟s16中得到的向量t被輸入到判定單元37。判定單元37判定向量t所包含的任意的子列ti是否為零向量(ti=0)(步驟s37)。在對任意的i=0、…、n-1,ti=0的情況下,判定單元37廢棄向量t(t不合格),將處理返回到步驟s12。另一方面,在對全部的i=0、…、n-1,ti≠0的情況下,向量t被發送到輸出單元18(t合格)。以後與實施方式1相同。
再者,與第二實施方式同樣地,步驟s37的等號判定也可以對每個i獨立地進行,但是也可以如圖2b所例示的那樣集中處理。在圖2b的例子中,判定單元37的集中等號判定單元對全部的i=0、…、n-1集中地進行是否ti=0的等號判定(集中等號判定),得到等號判定結果xi的列。其中,在ti=0的情況下xi=2k-1,在ti≠0的情況下xi=0(步驟s371)。之後的步驟s272~s275與第二實施方式相同。
另外,也可以是,集中等號判定單元在ti=0的情況下設為xi=0,在ti≠0的情況下設為xi=2k-1,聚合運算單元進行xi(其中,i=0、…、n-1)的聚合與運算(and運算),得到其運算結果、即聚合判定結果x。其中,在任意的等號判定結果xi(其中,i=0、…、n-1)為0的情況下x=0,在全部的等號判定結果xi(其中,i=0、…、n-1)為2k-1的情況下x=2k』-1。在該情況下,若x=0則聚合判定單元廢棄向量t(t不合格),將處理返回到步驟s12。另一方面,若x=2k-1則聚合判定單元將向量t發送到輸出單元18(t合格)。
<本方式的特徵>
本方式也與第二實施方式同樣地能夠高速地生成素域上的均勻隨機數。
[其他變形例等]
再者,本發明不限定於上述的實施方式。例如,也可以預先將梅森素數pi設定於隨機數生成裝置。在該情況下,能夠省略步驟s13及輸入單元13。進而,也可以預先將向量m設定於隨機數生成裝置。在該情況下,能夠進一步省略步驟s14及掩碼生成單元14。此外,也可以預先將二進位隨機數向量r存儲到存儲單元12中。此外,也可以使用作為合數的梅森數來取代梅森素數。例如,梅森數p0、…、pn-1可以全部是合數,梅森數p0、…、pn-1也可以包含素數和合數。
上述的各種處理不僅可以按照記載以時序予以執行,也可以與執行處理的裝置的處理能力或者需要相應地並行地或者單獨地予以執行。另外,不言而喻,在不脫離本發明的宗旨的範圍可以適當地變更。
在由計算機來實現上述的結構的情況下,由程序來記述各裝置所應該具有的功能的處理內容。通過由計算機來執行該程序,在計算機上實現上述處理功能。記述了該處理內容的程序能夠預先記錄於計算機可讀取的記錄介質。計算機可讀取的記錄介質的例子是非臨時性(non-transitory)的記錄介質。這樣的記錄介質的例子是磁記錄裝置、光碟、光磁記錄介質、半導體存儲器等。
該程序的流通例如是通過對記錄了該程序的dvd、cd-rom等的移動式記錄介質進行銷售、轉讓、租賃等而進行。進一步,也可以設為通過將該程序預先存儲到伺服器計算機的存儲裝置,經由網絡從伺服器計算機將該程序傳送到其他計算機,從而使該程序流通的結構。
執行這樣的程序的計算機例如首先將被記錄在移動式記錄介質中的程序或者從伺服器計算機傳送來的程序暫時存儲到自身的存儲裝置中。在執行處理時,該計算機讀取被存儲在自身的記錄裝置中的程序,執行依據讀取出的程序的處理。作為該程序的其他執行方式,也可以由計算機直接從移動式記錄介質讀取程序,執行依據該程序的處理,進一步,也可以是,每當程序被從伺服器計算機傳送到該計算機時,逐次執行依據所接收到的程序的處理。也可以設為通過所謂asp(applicationserviceprovider)型的服務來執行上述的處理的結構,該asp型的服務是指,不進行從伺服器計算機向該計算機的程序的傳送,僅通過其執行指示和結果獲取來實現處理功能。
在上述實施方式中,在計算機上執行規定的程序來實現了本裝置的處理功能,但是也可以由硬體來實現這些處理功能的至少一部分。
工業實用性
本發明例如可以利用於秘密分散、秘密計算、公鑰加密、對稱密鑰加密、電子署名等的各種加密技術。
標號說明
1~3隨機數生成裝置
