基於風光互補的混合能源系統優化方法與流程
2023-09-11 09:13:05 2
本發明涉及清潔能源混合系統,具體涉及一種基於風光互補的混合能源系統在隨機模型下的優化方法。
背景技術:
在偏遠地區,通過遠距離輸電線進行供電是比較困難且經濟效益較差的,而這些地區又缺乏電站,若選擇電網連接,其高昂的成本及複雜的地形也是一大難題,所以這就迫使人們尋求其他的方法來解決這個問題。基於可再生能源的獨立混合能源系統就成為了可滿足這些需求的可行方案。
可再生能源中,風能和太陽能在偏遠地區是較為豐富的,使用風能/太陽能可以減少燃料成本及傳統電網一部分的運行、維護成本。但所能節省的資本成本取決於風能/太陽能的可安裝容量,同時風能/太陽能其本身的不穩定性是混合能源系統的主要缺點。通常,使用電池組作為輔助能源以提高系統的穩定性,不過功率平衡問題對由間歇性發電裝置供能的獨立電網來說仍是一個難題。在獨立電網中需要安排更大容量的儲能設備以保證足夠的安全性及穩定性,不過大容量儲能設備也會導致投資和運行成本的增加,所以找到一個合適的容量使系統在穩定性和成本之間達到相對平衡的狀態就成為了需要解決的關鍵問題。
技術實現要素:
針對上述現狀與相關技術存在的問題,本發明對此提出了一種基於風光互補的混合能源系統設計優化方法。根據所設計的混合能源系統結構框圖,提出了通過風速、太陽輻射值和負載需求的歷史數據建立隨機數學模型,給出目標函數及約束條件,最後利用智能優化算法對函數進行求解,得出風/光/儲能系統的最優容量。在本發明中使用ARMA模型代表風速、太陽輻射值和負載需求的不確定性,用連續蒙特卡洛仿真(SMCS)模型按時間序列表示系統的狀態,其後列出目標函數使得混合能源系統的一次性投資成本和運行維護成本最低,同時將穩定性指標EENS也作為約束條件。本發明的創新點主要可總結為以下兩點:1)提出了一種基於自適應進化策略結合Fischer–Burmeister算法的優化方案;2)研究在不同的穩定性/負載轉移水平下儲能單元參數對系統投資成本的影響,從而讓決策者可以在滿足負載需求的前提下靈活的選擇合適的安裝容量,同時保持一個較低的投資成本。
為了實現上述目的,首先要建立隨機模型並且對其可靠性概率進行評估。ARMA模型是由自回歸模型(AR(p))和移動平均數法(MA(q))結合而成,該模型可通過負載、風速和太陽輻射值的歷史數據來預估負載需求、風速和太陽輻射值。混合能源系統的不確定性主要包括負載需求的變化、風速的變化、太陽輻射的變化、風力渦輪機和光伏板的設備故障率等問題,可通過計算穩定性指標EENS對其可靠性概率進行評估。
目標函數的設定是為了使在混合能源系統的整個運行周期中風/光/儲能系統的一次性投資成本和可變成本最低化。這些成本主要包括電池、風力渦輪機和光伏板的安裝及維護成本、柴油機的燃料消耗成本。
對之前建立的關於成本的目標函數可使用自適應進化策略(SAES)進行求解。該方法在種群中隨機選取一個父代,通過突變產生子代,在這些子代中選取最優的個體重複突變選擇過程,直到達到迭代次數,產生最優結果。但SAES的突變機制未將方案的可行性考慮在內,因此不具有可行性的後代會頻繁出現,此外,計算量方面的負擔也會很高,這是因為SAES的搜索容量取決於種群規模。故該算法可能會陷入局部最優的狀態。為了克服這些缺點,本發明採用Fischer-Burmeister優化方法結合SAES對該目標函數進行求解。
基於風光互補的混合能源系統優化方法,其特徵在於包括以下步驟:
步驟一、根據一個時間序列內可得到的負載需求/風速/太陽輻射值的歷史數據,再使用ARMA模型通過獲得的歷史數據對下一時序的負載需求/風速/太陽輻射值進行預測;ARMA(p,q)模型由自回歸模型(AR(p))和移動平均數法(MA(q))結合而成:
其中,yt表示預測值,用yt(1)、yt(2)和yt(3)分別表示負載/風速/太陽輻射值的預測值,統一以yt表示預測值進行數學計算;Φi是自回歸模型AR的係數,θj是移動平均數MA的係數,εt-j是常規的獨立分布式隨機白噪聲過程,該模型給出了在連續時間上任一點的值是先前p點和q白噪聲點的線性組合;
將過去一年內每個月的預測值數據分為一個個片段;在前一年每小時的時序安排內,ARMA模型的輸出值使用評價標準化誤差進行評價化與比例化處理;由式(1)計算出每小時負載/風速/太陽輻射值,如下式:St=μt+σtyt (2)
其中,μt、σt分別表示每小時預測值的平均值和標準誤差;
在已知某年數據的基礎上,通過前一年數據和ARMA模型進行預測後與真實數據進行對比,選出絕對百分比誤差最小的p,q參數,得到關於負載、風速和太陽輻射的ARMA模型;
步驟二、ARMA可靠性概率評估,包括以下子步驟:
2.1)風力渦輪機的初始狀態假設為啟動;
2.2)在風力渦輪機的一個狀態周期內進行採樣,狀態周期的採樣值由下式給出:其中D、R分別表示周期和[0,1]區間內的一個隨機數,γ表示基於現狀態下的中斷/維修率;
2.3)由ARMA負載模型給出負載需求樣本;
2.4)在一個時間序列中重複步驟2.2)和2.3),採樣結果按時間進行排序;
2.5)整個工作時序中所提供能量的中斷功率需求的累計值被定義為計算穩定性指標EENS並計算此值;
步驟三、列出目標函數:
其中,CES為儲能系統的成本,CPV為光伏板的安裝、維護成本,Cwt為風力渦輪機的安裝、維護成本;
CES=pbat×Qbat+(λbat×pbat+mbat)×Qbat
Cwt=IC×Pr+(IC×λwt+mwt)×Pr
CPV=ICC×Ppv+(ICC×λPV+mPV)×Ppv
其中,pbat、Qbat、λbat、mbat分別表示電池的單位價格、電池容量、電池的折現率、電池維護成本;IC、ICC表示風力渦輪機和光伏板的安裝成本,λwt、λPV表示風力渦輪機和光伏板的折現率,mwt、mPV表示風力渦輪機和光伏板的維護成本,Pr、Ppv表示風力渦輪機和光伏板的額定功率;
步驟四、根據列出的目標函數,限定各變量的約束條件,包括儲能約束和穩定性約束條件;電池的充放電過程約束條件如下:
若則
若則
儲能約束提供負載管理過程,分為以下幾個子步驟:4.1)若風能、太陽能所提供的功率未能滿足負載需求水平,同時電池內的儲能幾乎為零,則要採用負載轉移策略;4.2)轉移負載被傳遞到下一個時間區間;4.3)若在負載轉移之後仍不能滿足功率平衡,則再負載需求在一個特定的功率水平下被打斷;4.4)重複子步驟4.1-4.3,並對式(4)重新計算,直至達到功率平衡;
穩定性分析中的概率性指標EENS可通過下式計算:
其中,ENS表示未使用能量,N表示樣本數;據此給出下述穩定性約束:
EENS≤EENSmax (6)
步驟五、在給出了目標函數和約束條件之後,需要通過智能算法來解決;本發明運用自適應進化策略(SAES)進行對風速、太陽輻射和負載需求由ARMA模型所得的預測值進行初始化,然後再運用Fischer-Burmeister優化方法進行求解式(3)關於成本的目標函數,從而得到混合能源系統中光伏模塊、風力渦輪機和電池組的最優容量使整個系統的成本最低。
本發明的主要優點是:1)參考歷史數據所建立的ARMA模型相比於傳統數學模型更加準確;2)引入了穩定性指標EENS,使得整體模型的穩定性加以改善;3)Fischer-Burmeister優化方法結合SAES一起使用,在突變產生的後代個體中,具有高適應度的個體會被限定在Fischer-Burmeister優化方法所規定的約束範圍之內,相比於傳統方法,能夠在全局內求得最優結果,避免了局部最優的情況,同時計算量也大大減少,使得優化過程的速度得到增加。
附圖說明
圖1是本發明的混合能源系統結構示意圖;
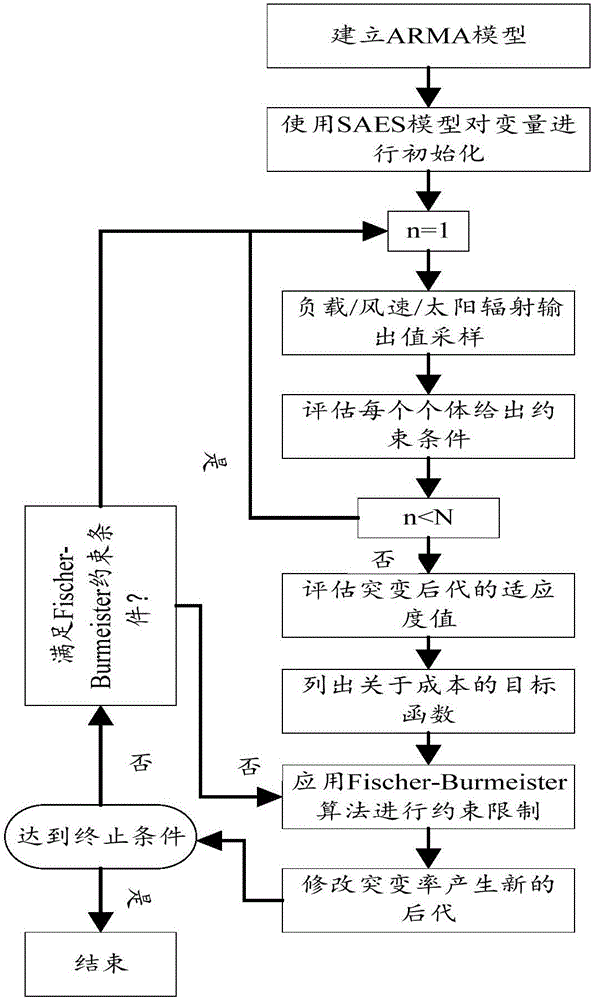
圖2是本發明基於風光互補的混合能源系統優化方法的流程圖;
具體實施方式
本發明的目的在於提出一種基於風/光互補的混合能源系統設計優化方法,根據所設計的混合能源系統結構框圖,如圖1所示,本發明的多能源系統主要由風能、太陽能和儲能電池組成,提出了通過風速、太陽輻射值和負載需求的歷史數據建立隨機數學模型,給出目標函數及約束條件,最後利用智能優化算法對函數進行求解,得出風/光/儲能系統的最優容量。如圖2所示,包括以下步驟:1、首先建立關於目標變量的ARMA模型。根據一個時間序列內可得到的負載需求/風速/太陽輻射值的歷史數據,使用ARMA模型通過獲得的歷史數據對下一時序的負載需求/風速/太陽輻射值進行預測。ARMA(p,q)模型由自回歸模型(AR(p))和移動平均數法(MA(q))結合而成:
其中,Φi是自回歸模型AR的係數,θj是移動平均數MA的係數,εt-j是常規的獨立分布式隨機白噪聲過程,該模型給出了在連續時間上任一點的值是先前p點和q白噪聲點的線性組合。
將過去一年內每個月的數據分為一個個片段,故在一個月內相同的時間有好幾個數據點。因此,在前一年每小時的時序安排內,ARMA模型的輸出值需使用評價標準化誤差進行評價化與比例化處理。由式(1)可計算出每小時負載/風速/太陽輻射值,見下式:
St=μt+σtyt (2)
其中,μt、σt分別表示每小時負載/風速/太陽輻射的平均值和標準誤差。
在已知某年數據的基礎上,通過前一年數據和ARMA模型進行預測後與真實數據進行對比,選出絕對百分比誤差最小的p,q參數,得到關於負載、風速和太陽輻射的最準確ARMA模型。
2、在建立了關於負載需求/風速/太陽輻射值的ARMA模型後,需要使用SAES模型對變量進行初始化,同時對負載/風速/太陽輻射值進行採樣,通過個體的約束條件對其可靠性概率進行評估。混合能源系統的不確定性主要包括負載需求的變化、風速的變化、太陽輻射的變化和風力渦輪機/光伏板設備故障率問題。其中,針對風力渦輪機可採用雙態模型來控制其啟-停順序,具體可分為以下步驟:
1)風力渦輪機的初始狀態假設為啟動;2)在風力渦輪機的一個狀態周期內進行採樣,狀態周期的採樣值由下式給出:其中D、R分別表示周期和[0,1]區間內的一個隨機數,γ表示基於現狀態下的中斷/維修率;3)由ARMA負載模型給出的負載需求樣本;4)在一個時間序列中重複步驟2)和3),採樣結果按時間進行排序;5)計算穩定性指標EENS。
3、根據發明目的列出目標函數。本發明的目標是使得基於風/光互補的混合能源系統在整個運行周期內一次性投資成本和可變成本最低,故據此可列出目標函數:
其中,CES為儲能系統的成本,CPV為光伏板的安裝、維護成本,Cwt為風力渦輪機的安裝、維護成本。
CES=pbat×Qbat+(λbat×pbat+mbat)×Qbat
Cwt=IC×Pr+(IC×λwt+mwt)×Pr
CPV=ICC×Ppv+(ICC×λPV+mPV)×Ppv
其中,pbat、Qbat、λbat、mbat分別表示電池的單位價格、電池容量、電池的折現率、電池維護成本。IC、ICC表示風力渦輪機和光伏板的安裝成本,λwt、λPV表示風力渦輪機和光伏板的折現率,mwt、mPV表示風力渦輪機和光伏板的維護成本,Pr、Ppv表示風力渦輪機和光伏板的額定功率。
4、根據列出的目標函數,限定各變量的約束條件,主要可分為儲能約束和穩定性約束。電池的充放電過程如下:
若則
若則
儲能約束提供負載管理過程分為以下幾部分:1)若風能、太陽能所提供的功率未能滿足負載需求水平,同時電池內的儲能幾乎為零,則要採用負載轉移策略;2)轉移負載被傳遞到下一個時間區間;3)若在負載轉移之後仍不能滿足功率平衡,則再負載需求在一個特定的功率水平下被打斷;4)重複1-3步並對式(4)重新計算,直至達到功率平衡。
而在整個工作時序中中斷功率需求的累計值被定義為提供能量(EENS),所以EENS在穩定性分析中是一個概率性指標:
其中,ENS表示未使用能量,N表示樣本數。據此,可給出下述穩定性約束:
EENS≤EENSmax (6)
5、在給出了目標函數和約束條件之後,需要通過智能算法來解決這樣一個數學問題。本發明運用自適應進化策略(SAES)進行變量初始化,然後再運用Fischer-Burmeister優化方法進行求解關於成本的目標函數,從而得到混合能源系統中光伏模塊、風力渦輪機和電池組的最優容量使整個系統的成本最低。具體步驟如下:1)列出風速、太陽輻射和負載需求的ARMA模型;2)通過SAES對參數進行初始化操作;3)在一個周期內進行採樣,對每個採樣數據給出約束條件,若違反約束條件分配出一個不可行的方案,則需要給目標函數附加一個較大的補償係數;4)估算突變後代的適應度值,並應用Fischer-Burmeister優化方法進行約束限制,以對突變率進行相應的修改;5)重複該過程直至滿足終止條件;6)得出個體的最優適應度值。
本發明的主要優點是:1)參考歷史數據所建立的ARMA模型相比於傳統數學模型更加準確;2)引入了穩定性指標EENS,使得整體模型的穩定性加以改善;3)Fischer-Burmeister優化方法結合SAES一起使用,在突變產生的後代個體中,具有高適應度的個體會被限定在Fischer-Burmeister優化方法所規定的約束範圍之內,相比於傳統方法,能夠在全局內求得最優結果,避免了局部最優的情況,同時計算量也大大減少,使得運算速度得到增加。
