循環流化床生活垃圾焚燒鍋爐床溫預測方法及系統與流程
2023-08-06 10:00:51 1
本發明涉及能源工程領域,特別地,涉及一種循環流化床生活垃圾焚燒鍋爐床溫預測方法及系統。
背景技術:
垃圾焚燒由於能夠良好實現垃圾處理技術的減容化、減量化、無害化和資源化,近十幾年內,在國家相關產業政策的引導下,國內垃圾焚燒行業取得了蓬勃的發展。從上世紀90年代開始,國內多家科研結構對中國城市生活垃圾(Municipal Solid Waste,MSW)燃燒機理進行了大量深入研究,掌握了混合收集、水分高、成分複雜的城市生活垃圾的燃燒特性,根據我國對煤、煤矸石等劣質燃料循環流化床(Circulating Fluidized Bed,CFB)燃燒技術的開發經驗的基礎上,開發出了循環流化床垃圾焚燒鍋爐,從1998年浙江大學開發的第一臺流化床垃圾焚燒爐投入運行開始,表現出了適用於對國內高水分、熱值偏低且波動性很大的生活垃圾進行大規模的焚燒處理的特點。目前,CFB垃圾焚燒技術已經在國內的多個城市進行了推廣應用,截止2014年底,國內已建成垃圾焚燒鍋爐70餘臺,日處理垃圾量6.4萬噸,為我國的垃圾焚燒處理行業做出了重要的貢獻。
床溫是一個影響循環流化床垃圾焚燒鍋爐安全、環保、經濟運行的重要運行參數,一般要求流化床鍋爐的床層運行溫度控制在850-950℃之間,床層溫度太低不利於垃圾的充分乾燥以及揮發分的析出燃燒和殘碳的燃燒,難以保證垃圾中有害物質被徹底分解,對鍋爐燃燒穩定性造成不良影響,同時,也不利於鍋爐蒸汽品質的提升;床層溫度太高則會帶來高溫結渣、腐蝕和增加爐體負擔等問題。另一方面,為了促進垃圾焚燒企業運行管理水平的發展,提升垃圾焚燒工藝的安全性、環保性和經濟性,國家住建部頒發的《生活垃圾焚燒廠評價標準(CJJ/T 137–2010)》中,對生活垃圾焚燒系統設置了是否配套了自動燃燒控制系統(Automatic Combustion Control,ACC)的評分選項,而循環流化床生活垃圾焚燒鍋爐ACC系統中有一個重要的子控制系統就是床溫控制系統,而實施床溫控制系統的一項重要前提就是構建足夠精度的實時床溫預測模型。因此,構建一個實用的床溫特性模型具有十分重要的意義。
國內外的研究人員對循環流化床鍋爐的床溫特性建模進行了研究。目前,床溫的特性建模主要有以下幾種方法。一種是根據CFB鍋爐燃燒動力學、流體力學、傳熱傳質的特性,在經過合理的簡化假設之後建立,通過數學描述的方式建立機理模型。這種方法能夠反映床溫的變化趨勢,但由於假設模型和真實模型之間的偏差而無法達到足夠的精確度;另一種方法是在大量的試驗臺試驗或者現場試驗的基礎上,通過回歸分析的方法建立關於床溫變化特性的經驗模型。這種方法需要耗費大量的人力物力,時間成本高,同時無法保證試驗覆蓋所有的工況,具有一定局限性;第三種方法利用計算流體力學、計算傳熱學和化學反應的簡化機理模擬爐內燃燒過程,精確地求解床層溫度場的分布情況,顯示了良好的效果具有很大的發展潛力。但這種方法主要受限於流體力學模型和化學反應的簡化機理與實際情況的差距,需要高端的計算機配置和很長的計算時間,因此採用這種方法仍處於初步發展階段。此外,CFB垃圾焚燒鍋爐的給料系統均勻性較差,入爐垃圾的熱值波動性大、組分複雜、多邊性強,是床溫建模過程中的面臨的主要困難之一,它要求所建立的床溫特性模型具有良好的自適應能力,上述三種建模方法在這方面仍有所欠缺。
隨著電子技術、計算機技術和信息技術的發展,集散控制系統(Distributed Control System,DCS)廣泛的應用於CFB生活焚燒鍋爐的運行過程,包含溫度、壓力、流量等參數在內的過程數據都被完善得保存下來,這些歷史數據中包含豐富過程信息,是人們認識和了解生產過程的重要途徑之一,具有很高的挖掘價值。自適應糊神經網絡(Adaptive Neuro-Fuzzy Inference System,ANFIS)融合了神經網絡並行計算、分布式信息存儲、容錯能力強、具備自適應學習功能等優點和模糊算法能夠有效表達先驗知識的能力,成為構建不確定性和非線性模型的有力工具。同時,ANFIS模型的訓練所需的時間較短,無需配置高端的計算機即可完成訓練任務,訓練好的模型能夠勝任在線預測工作。因此,基於ANFIS算法的床溫預測模型可以滿足實際生產過程對模型的實時性要求。然而,ANFIS床溫預測模型在設計時面臨著模型輸入變量難以選擇、模型的初始結構確認困難以及訓練樣本大小難以確定等問題。輸入變量冗餘過多,一方面會增加模型的複雜度,另一方面會引入數據噪聲,甚至淹沒了數據中的有效信息,使模型的性能退化;輸入變量選擇過少則無法構成完備床溫表達模型,產生欠擬合。而要確認ANFIS模型的初始結構則需要在大量的訓練樣本中分析並提煉出模糊規則,這要求建模人員深入掌握CFB生活垃圾焚燒鍋爐的運行機理,並且需要耗費大量的時間,大大增加了建模過程的複雜程度和難度。訓練樣本過多,會大幅度延長模型的訓練時間,並且有可能會引入噪聲數據,導致產生過擬合現象;訓練樣本過少,模型無法獲取足夠的信息支撐,是模型的泛化性能下降。
技術實現要素:
本發明的目的在於針對現有技術的不足,提供一種循環流化床生活垃圾焚燒鍋爐床溫的預測方法及系統。本發明在分析CFB生活垃圾焚燒鍋爐運行機理的基礎上,初步選擇床溫預測模型的輸入變量,並利用Gamma Test算法進一步確定選擇模型的輸入變量和訓練樣本的個數,之後利用減法聚類算法對訓練樣本數據進行特徵提取,自適應的確定初始模糊規則和模糊神經網絡的初始結構參數,再結合最小二乘估計法和誤差反向傳播算法對模糊神經網絡的參數行學習訓練,並在這個過程中利用粒子群優化算法對減法聚類算法的聚類半徑進行尋優。
本發明的目的是通過以下技術方案來實現的:一種循環流化床生活垃圾焚燒鍋爐床溫預測方法,該方法包括以下步驟:
1)分析循環流化床生活垃圾焚燒鍋爐的運行機理,初步選擇垃圾的給料量、給煤量、一次風量、二次風量以及排渣量作為床溫預測模型的輸入變量。
2)採集訓練樣本。按設定的時間間隔從資料庫中採集輸入變量的歷史數據,或者採集指定工況下的運行參數,組成床溫預測模型輸入變量的訓練樣本矩陣X(m×n),m表示樣本個數,n表示變量的個數,同時採集與之對應的床層溫度作為模型的輸出變量,通常,床溫有較多的測點,取它們的平均值作為模型最終的輸出訓練樣本Y(m×1);
3)數據預處理。對X(m×n)進行粗大誤差處理和隨機誤差處理,以摒除那些並不是反映鍋爐正常運行工況的虛假信息,將鍋爐停爐、壓火、給料機堵塞等異常工況排除掉,為了避免預測模型的參數之間量綱和數量級的不同對模型性能造成的不良影響,訓練樣本輸入變量均經過歸一化處理後映射到[0,1]區間內,得到標準化後的輸入變量的訓練樣本X*(m×n)和輸出變量的訓練樣本Y*(m×1)。
4)智能算法集成建模。採用Gamma Test算法、粒子群優化算法(Particle Swarm Optimization,PSO)、減法聚類算法(Subtractive Clustering,SC)和模糊自適應神經網絡(Adaptive Neuro-Fuzzy Inference System,ANFIS)算法集成建模,確定模型最終的輸入變量的個數和訓練樣本的個數,並根據最終確定的訓練樣本進行參數尋優和學習,構建能夠表徵循環流化床生活垃圾焚燒鍋爐床溫特性的預測模型。該建模算法先利用Gamma Test算法尋找最優的模型輸入變量組合以及訓練樣本尺寸,然後採用減法聚類算法對樣本數據進行特徵提取,自適應的確定初始模糊規則和模糊神經網絡的初始結構參數,再結合最小二乘估計法和誤差反向傳播算法對模糊神經網絡的參數進行學習訓練。其中,聚類半徑是影響建模性能的關鍵參數,因此以預測精度為目標,利用PSO算法尋找聚類半徑的最優值。算法步驟如下:
4.1)利用Gamma Test算法尋找最優的模型輸入變量組合以及訓練樣本尺寸。Gamma Test算法是對所有光滑函數均適用的非參數估計方法,該方法不關注輸入輸出數據之間的任何參數關係,只對輸入輸出數據進行計算即可得到模型的噪聲方差,對於如下形式的數據集
{(Xi,Yi),1≤i≤m} (2)
式中,X∈Rn表示輸入,對應的輸出標量為y∈R。
Gamma Test假定的模型關係是:
y=f(x1,…,xn)+r (3)
式中,f是一個光滑函數,r是一個表示數據噪聲的隨機量。不失一般性,可假定r的均值為0(否則可在f中加入常數項),方差為Var(y)。Gamma Test就是計算一個統計量Γ,用它來評價輸出量的方差,顯然,如果數據的關係符合光滑模型,並且沒有噪聲,這個方差是0。Γ的計算過程如下:
4.1.1)計算輸入數據的距離統計量。用xi表示第i個輸入數據,xN[i,k]表示輸入樣本的第k近鄰域點,計算如下統計量:
<![CDATA[ δ m ( k ) = 1 m Σ i = 1 m | x N i , k - x i | 2 , 1 ≤ i ≤ m , 1 ≤ k ≤ p - - - ( 4 ) ]]>
式中,|·|表示歐拉距離,p為最遠鄰近距離(nearest neighbor)。
4.1.2)計算輸出數據的距離統計量。用yi表示第i個輸出數據,yN[i,k]表示輸出樣本的第k近鄰域點,計算如下統計量:
<![CDATA[ γ m ( k ) = 1 m Σ i = 1 m | y N i , k - y i | 2 , 1 ≤ i ≤ m , 1 ≤ k ≤ p - - - ( 5 ) ]]>
式中符號的意義同(4)式。
4.1.3)計算統計量Γ。為了計算Γ,分別計算鄰近距離從1到p的統計量(δm(1),γm(1)),(δm(2),γm(2)),…,(δm(p),γm(p))。對這p個統計量構造一元線性回歸模型,用最小二乘法進行擬合,得到的一次線性函數的截距就是Gamma Test統計量Γ,Γ值越小表示樣本中的噪聲越小。
定義另一個統計量Vratio:
式中,δ2(y)表示輸出y的方差。Vratio可以用來評價光滑模型對該數據的模擬能力,Vratio越接近0,表示該模型的預測性能越好。
首先,確定最優的訓練樣本尺寸。計算樣本量逐漸增大時Γ值的變化情況,當Γ值趨於穩定時,得到的樣本尺寸就是最優的訓練樣本尺寸。其次,確定最優的模型輸入變量組合。需要計算所有輸入變量組合時的Γ值和Vratio值,選擇Γ值和Vratio值都很小的組合作為模型的最終輸入變量。
4.2)利用PSO算法尋找最優的聚類半徑。以聚類半徑rα作為粒子,15個粒子作為一個種群,每個粒子隨機賦予[0.2 0.9]區間內的隨機值,其中第i個粒子的位置的向量標示為ri,i=1,2,…,15;
4.3)以ri為聚類半徑,進行減法聚類分析。減法聚類算法用於對建模數據樣本的空間進行初始劃分以及模糊規則的確定,K-均值聚類算法和模糊C-均值聚類算法均需預設聚類中心的數目,沒有充分利用樣本空間的蘊含的對象特徵信息。而減法聚類算法是一種基於山峰函數的聚類算法,它將每個數據點作為可能的聚類中心,並根據各個數據點周圍的數據點密度來計算該點作為聚類中心的可能性。
每個數據點Xi作為聚類中心的可能性Pi由式(7)來定義:
式中m表示n維輸入空間中全部的數據點數,Xi=[Xi1,Xi2,...,Xin]、Xj=[Xj1,Xj2,...,Xjn]是具體的數據點,ri是一個正數,定義了該點的鄰域半徑,||·||符號表示歐式距離。被選為聚類中心的點具有最高的數據點密度,同時該該數據點周圍的點被排除作為聚類中心的可能性。第一個聚類中心為XC1,數據點密度為Pc1。選出第一個聚類中心後,繼續採用類似的方法確定下一個聚類中心,但需消除已有聚類中心的影響,修改密度指標的山峰函數如下:
其中,rβ定義了一個密度指標顯著減小的鄰域,為了避免出現十分接近的聚類中心,rβ=1.5ri。循環重複上述過程直到所有剩餘數據點作為聚類中心的可能性低於某一閾值δ,即Pck/Pc1<δ。
4.4)ANFIS模型訓練。根據減法聚類算法得到的聚類中心,按照ANFIS模型結構訓練床溫預測模型;對於模糊神經網絡模型的所有參數,採用混合最小二乘法的梯度下降算法進行學習。
4.5)計算適應度值。利用訓練得到的預測模型計算垃圾熱值將床溫預測值與實際測量值y*進行比較,並以誤差平方和作為粒子的適應度值MSE,適應度計算公式如下:
4.6)更新極值。以適應度值為評價指標,比較當代粒子與上一代粒子之間的適應度值大小,如果當前粒子的適應度值優於上一代,則將當前粒子的位置設置為個體極值,否則個體極值保持不變。同時獲取當代所有粒子適應度值最優的粒子,並與上一代最優粒子進行比較,如果當代最優粒子的適應度值優於上一代最優粒子的適應度值,則將當代粒子的最優適應度值設置為全局最優值,否則全局最優值保持不變。
4.7)更新粒子。根據最新的個體極值和全局極值,按照(17)式和(18)式更新粒子的速度vid(t)和位置xid(t)。
vid(t+1)=ωvid(t)+c1r1(pid-xid(t))+c2r2(pgd-xid(t)) (17)
xid(t+1)=xid(t)+vid(t+1) (18)
t是粒子群優化算法的尋優代數。更進一步,為了改善基本粒子群算法容易陷入局部極值和收斂速度慢的缺陷,在PSO算法的基礎上引進了動態加速常數c1、c2和慣性權重ω:
其中,Tmax為最大尋優代數,ωmax為最大慣性權重,ωmin為最小慣性權重,R1、R2、R3、R4為常數。
4.8)算法停止條件算法判定。判斷是否達到最大迭代次數或者到達預測精度的要求,如果沒有達到則返回步驟4.3),利用更新的聚類半徑繼續搜索,否則退出搜索。
4.9)利用最終尋優得到的聚類半徑,對樣本進行聚類分析和ANFIS模型訓練,得到滿足訓練終止條件的ANFIS模型,即床溫預測模型。
5)預測床溫。對指定的樣本進行床溫預測,或者對當前鍋爐運行工況下的床溫進行實時預測。
一種循環流化床生活垃圾焚燒鍋爐床溫預測系統。該系統與循環流化床鍋爐的集散控制系統相連,包括數據通訊接口和上位機,所述上位機包括:
第一信號採集模塊。利用該模型採集CFB生活垃圾焚燒鍋爐在正常運行時的運行工況狀態參數和操作變量,並組成床溫預測模型輸入變量的訓練樣本矩陣X(m×n),和輸出訓練樣本矩陣Y(m×1),m表示樣本個數,n表示變量的個數。
數據預處理模塊。對訓練樣本進行粗大誤差處理和隨機誤差處理,剔除訓練樣本中的野值,排除異常工況,將訓練樣本輸入變量經歸一化處理後映射到[0,1]區間內,得到標準化後的訓練樣本X*(m×n)和Y*(m×1)。
專家知識庫模塊。將X*和Y*共同組成床溫預測模型的訓練樣本,並進行保存。
智能學習模塊。智能學習模塊是床溫預測系統的核心部分,該模塊先利用Gamma Test算法尋找最優的模型輸入變量組合以及訓練樣本尺寸,然後採用減法聚類算法對樣本數據進行特徵提取,自適應的確定初始模糊規則和模糊神經網絡的初始結構參數,再結合最小二乘估計法和誤差反向傳播算法對模糊神經網絡的參數進行學習訓練。其中,聚類半徑是影響建模性能的關鍵參數,因此以預測精度為目標,利用PSO算法尋找聚類半徑的最優值。算法步驟如下:
2.1)利用Gamma Test算法尋找最優的模型輸入變量組合以及訓練樣本尺寸。Gamma Test算法是對所有光滑函數均適用的非參數估計方法,該方法不關注輸入輸出數據之間的任何參數關係,只對輸入輸出數據進行計算即可得到模型的噪聲方差,對於如下形式的數據集
{(Xi,Yi),1≤i≤m} (2)
式中,X∈Rn表示輸入,對應的輸出標量為y∈R。
Gamma Test假定的模型關係是:
y=f(x1,…,xn)+r (3)
式中,f是一個光滑函數,r是一個表示數據噪聲的隨機量。不失一般性,可假定r的均值為0(否則可在f中加入常數項),方差為Var(y)。Gamma Test就是計算一個統計量Γ,用它來評價輸出量的方差,顯然,如果數據的關係符合光滑模型,並且沒有噪聲,這個方差是0。Γ的計算過程如下:
2.1.1)計算輸入數據的距離統計量。用xi表示第i個輸入數據,xN[i,k]表示輸入樣本的第k近鄰域點,計算如下統計量:
<![CDATA[ δ m ( k ) = 1 m Σ i = 1 m | x N i , k - x i | 2 , 1 ≤ i ≤ m , 1 ≤ k ≤ p - - - ( 4 ) ]]>
式中,|·|表示歐拉距離,p為最遠鄰近距離(nearest neighbor)。
2.1.2)計算輸出數據的距離統計量。用yi表示第i個輸出數據,yN[i,k]表示輸出樣本的第k近鄰域點,計算如下統計量:
<![CDATA[ γ m ( k ) = 1 m Σ i = 1 m | y N i , k - y i | 2 , 1 ≤ i ≤ m , 1 ≤ k ≤ p - - - ( 5 ) ]]>
式中符號的意義同(4)式。
2.1.3)計算統計量Γ。為了計算Γ,分別計算鄰近距離從1到p的統計量(δm(1),γm(1)),(δm(2),γm(2)),…,(δm(p),γm(p))。對這p個統計量構造一元線性回歸模型,用最小二乘法進行擬合,得到的一次線性函數的截距就是Gamma Test統計量Γ,Γ值越小表示樣本中的噪聲越小。
定義另一個統計量Vratio:
式中,δ2(y)表示輸出y的方差。Vratio可以用來評價光滑模型對該數據的模擬能力,Vratio越接近0,表示該模型的預測性能越好。
首先,確定最優的訓練樣本尺寸。計算樣本量逐漸增大時Γ值的變化情況,當Γ值趨於穩定時,得到的樣本尺寸就是最優的訓練樣本尺寸。其次,確定最優的模型輸入變量組合。需要計算所有輸入變量組合時的Γ值和Vratio值,選擇Γ值和Vratio值都很小的組合作為模型的最終輸入變量。
2.2)利用PSO算法尋找最優的聚類半徑。以聚類半徑rα作為粒子,15個粒子作為一個種群,每個粒子隨機賦予[0.2 0.9]區間內的隨機值,其中第i個粒子的位置的向量標示為ri,i=1,2,…,15;
2.3)以ri為聚類半徑,進行減法聚類分析。減法聚類算法用於對建模數據樣本的空間進行初始劃分以及模糊規則的確定,K-均值聚類算法和模糊C-均值聚類算法均需預設聚類中心的數目,沒有充分利用樣本空間的蘊含的對象特徵信息。而減法聚類算法是一種基於山峰函數的聚類算法,它將每個數據點作為可能的聚類中心,並根據各個數據點周圍的數據點密度來計算該點作為聚類中心的可能性。
每個數據點Xi作為聚類中心的可能性Pi由式(7)來定義:
式中m表示n維輸入空間中全部的數據點數,Xi=[Xi1,Xi2,...,Xin]、Xj=[Xj1,Xj2,...,Xjn]是具體的數據點,ri是一個正數,定義了該點的鄰域半徑,||·||符號表示歐式距離。被選為聚類中心的點具有最高的數據點密度,同時該該數據點周圍的點被排除作為聚類中心的可能性。第一個聚類中心為XC1,數據點密度為Pc1。選出第一個聚類中心後,繼續採用類似的方法確定下一個聚類中心,但需消除已有聚類中心的影響,修改密度指標的山峰函數如下:
其中,rβ定義了一個密度指標顯著減小的鄰域,為了避免出現十分接近的聚類中心,rβ=1.5ri。循環重複上述過程直到所有剩餘數據點作為聚類中心的可能性低於某一閾值δ,即Pck/Pc1<δ。
2.4)ANFIS模型訓練。根據減法聚類算法得到的聚類中心,按照ANFIS模型結構訓練床溫預測模型;對於模糊神經網絡模型的所有參數,採用混合最小二乘法的梯度下降算法進行學習。
2.5)計算適應度值。利用訓練得到的預測模型計算垃圾熱值將床溫預測值與實際測量值y*進行比較,並以誤差平方和作為粒子的適應度值MSE,適應度計算公式如下:
2.6)更新極值。以適應度值為評價指標,比較當代粒子與上一代粒子之間的適應度值大小,如果當前粒子的適應度值優於上一代,則將當前粒子的位置設置為個體極值,否則個體極值保持不變。同時獲取當代所有粒子適應度值最優的粒子,並與上一代最優粒子進行比較,如果當代最優粒子的適應度值優於上一代最優粒子的適應度值,則將當代粒子的最優適應度值設置為全局最優值,否則全局最優值保持不變。
2.7)更新粒子。根據最新的個體極值和全局極值,按照(17)式和(18)式更新粒子的速度vid(t)和位置xid(t)。
vid(t+1)=ωvid(t)+c1r1(pid-xid(t))+c2r2(pgd-xid(t)) (17)
xid(t+1)=xid(t)+vid(t+1) (18)
t是粒子群優化算法的尋優代數。更進一步,為了改善基本粒子群算法容易陷入局部極值和收斂速度慢的缺陷,在PSO算法的基礎上引進了動態加速常數c1、c2和慣性權重ω:
其中,Tmax為最大尋優代數,ωmax為最大慣性權重,ωmin為最小慣性權重,R1、R2、R3、R4為常數。
2.8)算法停止條件算法判定。判斷是否達到最大迭代次數或者到達預測精度的要求,如果沒有達到則返回步驟4.3),利用更新的聚類半徑繼續搜索,否則退出搜索。
2.9)利用最終尋優得到的聚類半徑,對樣本進行聚類分析和ANFIS模型訓練,得到滿足訓練終止條件的ANFIS模型,即床溫預測模型。
第二信號採集模塊。用於從資料庫中選擇需要預測床溫的運行工況,或者實時地採集當前鍋爐的運行工況。
預測模塊。該模塊用於對指定的樣本進行床溫預測,或者對當前鍋爐運行工況下的床溫進行實時預測。
結果顯示模塊。顯示床溫的預測結果,或者對床溫的預測結果進行統計分析。
本發明的有益效果是:在利用循環流化床生活垃圾焚燒鍋爐的運行機理和運行歷史數據中隱含的知識的基礎上,採用Gamma Test算法、PSO算法、減法聚類算法和ANFIS算法集成建模的方法,構建了一種快速經濟的方法和系統對鍋爐床溫進行實時預測,避開了繁瑣複雜的機理建模工作。其中,利用ANFIS算法的自學習能力、非線性映射能力、泛化能力和實時預測能力來表徵床溫的動態變化特性,為運行人員和設計人員掌握了解床溫的變化特新提供新的途徑;利用減法聚類算法自適應的確定ANFIS模型的初始結構和參數,避免了複雜繁瑣的人工設計工作;利用PSO算法尋找最優的聚類半徑,保證獲取最優的ANFIS模型結構;利用Gamma Test算法獲取最優的訓練樣本,避免了模型的在訓練的時候出現過擬合和欠擬合的狀況。整個建模過程邏輯清晰,需要設置的參數較少,建模自動化程度高,易於掌握和推廣。同時,訓練良好的ANFIS床溫預測模型可以服務那些基於模型的控制算法,為循環流化床生活垃圾焚燒鍋爐的ACC系統實施提供幫助。
附圖說明
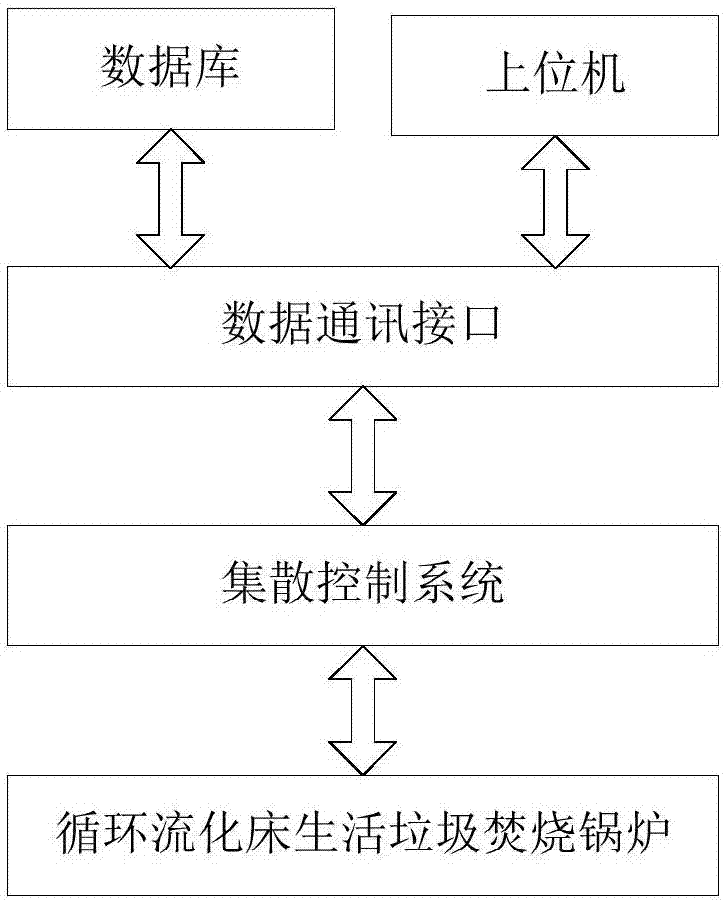
圖1是本發明所提出的系統的結構圖。
圖2是本發明所提出的上位機系統的結構圖。
圖3是本發明所採用ANFIS模型的系統結構圖。
圖4是本發明所提出的智能建模方法的流程圖。
具體實施方式
下面結合附圖和具體實施例對本發明作進一步詳細說明。
實施例1
參照圖1、圖2、圖3、圖4,本發明提供的一種循環流化床生活垃圾焚燒鍋爐床溫預測方法,該方法包括以下步驟:
1)分析循環流化床鍋爐的運行機理,初步選擇床溫預測模型的輸入變量。國內的城市生活垃圾多為混合收集,導致入廠、入爐垃圾成分較為複雜,一般主要包括廚餘垃圾、紙、塑料、橡膠、織物、木頭、竹子以及無機物等主要成分,表現出低熱值、高水分和波動性較大的特徵。為了保證循環流化床垃圾焚燒鍋爐的穩定燃燒,通常會添加煤作為輔助燃料。垃圾在循環流化床中的燃燒是一個十分複雜的劇烈物理化學變化過程,垃圾在進入爐膛之後會經歷幾個過程:乾燥加熱、揮發分析出及燃燒、焦炭燃燒。垃圾中質輕易碎的組分如紙紙張、塑料以及細顆粒等會在流化風的作用下進入爐膛上部,經歷乾燥、揮發分的析出及燃燒以及殘炭的燃燒等一系列過程;而密度較大、含水率高以及顆粒尺寸較大的組分如木頭、廚餘垃圾等終端速度大於流化速度的組分會落入密相區,並在密相區中被床料加熱、燃燒,與煤的熱量釋放規律不同,垃圾中高水分低熱值的組分會在密相區中吸收大量的熱,而大量的揮發分在懸浮段燃燒。CFB鍋爐的床溫是由幾部分熱量的平衡關係決定的:布風板上煤和垃圾燃燒釋放的熱量、煤和垃圾乾燥吸收的熱量、一次風形成煙氣帶走的熱量、水冷壁吸收的熱量、返料器返料帶回的熱量、爐膛排渣帶走的熱量以及爐膛散熱,同時還受到鍋爐設計參數的影響。但在實際運行過程當中,一般鍋爐設計參數是不可調整的,在一定時間內爐膛散熱也可以看成是不變的,所以,影響床溫的主要是鍋爐的運行參數,尤其是給煤機、垃圾給料機和送風機等執行機構的參數。
鍋爐運行期間,給煤量增加初期,會因為自身的乾燥加熱而吸收部分熱量,但隨著燃燒過程的進行,揮發分的燃燒會釋放出的熱量,同時密相區的殘碳積累量增加會逐漸增加,所以給煤量的增加會使床溫先降後升。增加垃圾給料量對床溫造成的影響比較複雜,由於垃圾的組分比較複雜,通常,含水量低且可燃成分高的生活垃圾,在進入爐膛之後,能夠通過自身燃燒釋放的熱量彌補乾燥加熱吸收的熱量,保證床溫的穩定;而含水量高且可燃成分低的生活垃圾進入爐膛之後,由於自身釋放的熱量難以平衡乾燥加熱吸收的熱量,會持續地降低床溫。通常密相區為缺氧燃燒,一次風量增加能夠使燃燒反應加劇,煤和垃圾中的可燃成分燃燒釋放的熱量增加,但一次風是冷風,且一次風量的增加會同使煙氣和細床料帶走的熱量也增加,所以隨著密相區中焦炭池的消耗,一次風量增加實際上起到降低爐溫的作用。二次風主要為稀相區的燃燒反應提供氧量,當氧量充足的時候,由於二次風是冷風,增加二次風會降低煙氣和流化物料的溫度;當氧氣含量不足的時候,增加二次風能夠促進稀相區中揮發分和殘碳的燃燒,從而提高煙氣溫度和流化床料的溫度。而部分的煙氣和流化物料會通過物料分離器回到密相區,所以改變二次風量能夠間接地影響床溫。由於CFB垃圾焚燒鍋爐循環物料的溫度與床溫不同,通常返料量是通過物料分離器的分離效率來保證的,並通過返料風來維持料腿的高度,所以返料風量在一定程度上能夠表徵返料量的大小,但是在實際運行過程當中,返料風量通常保持恆定的值,難以體現出來對床溫的影響。CFB垃圾焚燒鍋爐的床料量主要通過垃圾中的泥土、石塊、玻璃等不可燃的惰性物組成,並通過排渣機將最底層的床料排出爐膛,以此來維持爐膛中的床料的平衡,料層太薄,床料的蓄熱量不夠,不利於垃圾的乾燥燃燒和床溫的穩定控制,同時易造成布風不均勻,流化情況惡化,導致結焦情況的發生;料層太厚,大塊的不可燃顆粒不能及時排出爐膛,同樣會導致爐內流化情況的惡化,同時增加了風機的電耗。為了保證床溫維持在較高的水平,促進垃圾的乾燥燃盡,CFB垃圾焚燒鍋爐會在密相區的水冷壁澆築隔熱層,所以,當外界擾動造成床溫波動時,短時間內可以忽略密相區水冷壁吸熱對床溫造成的影響。
綜上所述,初步選擇垃圾的給料量、給煤量、一次風量、二次風量以及排渣量作為ANFIS床溫預測模型的輸入變量。
2)採集訓練樣本。按設定的時間間隔從資料庫中採集相關變量的歷史數據,或者採集指定工況下的運行參數,組成垃圾熱值預測模型輸入變量的訓練樣本矩陣X(m×n),m表示樣本個數,n表示變量的個數,同時採集與之對應的床層溫度作為模型的輸出變量,通常,床溫有較多的測點,取它們的平均值作為模型最終的輸出訓練樣本Y(m×1);
3)數據預處理。對X(m×n)進行粗大誤差處理和隨機誤差處理,以摒除那些並不是反映鍋爐正常運行工況的虛假信息,將鍋爐停爐、壓火、給料機堵塞等異常工況排除掉,為了避免預測模型的參數之間量綱和數量級的不同對模型性能造成的不良影響,訓練樣本輸入變量均經過歸一化處理後映射到[0,1]區間內,得到標準化後的輸入變量的訓練樣本X*(m×n)和輸出變量的訓練樣本Y*(m×1)。預處理過程採用以下步驟進行:
3.1)根據拉伊達準則,剔除訓練樣本X(m×n)和Y(m×1)中的野值;
3.2)剔除鍋爐停爐運行工況,鍋爐停爐時爐膛給煤機和給料機的開度為零,並且爐膛中溫度接近常溫;
3.3)剔除爐膛壓火運行狀況,鍋爐壓火時一次風機、二次風機引風機爐膛給煤機和給料機的開度為零,但是爐膛密相區的溫度維持在350℃~450℃;
3.4)剔除給料機堵塞工況,給料機堵塞需要運行人員通過給料口的攝像頭拍攝的畫面對給料情況進行判斷,給料機堵塞時,運行人員會顯著地調高給料機的開度,反映在運行數據上,即給料機的開度大於35%;
3.5)數據歸一化處理。按照式(1)將數據變量映射到[0 1]的區間內。
式中XJ表示第J變量所組成的向量,min表示最小值,max表示最大值。
4)智能算法集成建模。採用Gamma Test算法、粒子群優化算法(Particle Swarm Optimization,PSO)、減法聚類算法(Subtractive Clustering,SC)和模糊自適應神經網絡(Adaptive Neuro-Fuzzy Inference System,ANFIS)算法集成建模,確定模型最終的輸入變量的個數和訓練樣本的個數,並根據最終確定的訓練樣本進行參數尋優和學習,構建能夠表徵循環流化床生活垃圾焚燒鍋爐床溫特性的預測模型。
該建模算法先利用Gamma Test算法尋找最優的模型輸入變量組合以及訓練樣本尺寸,然後採用減法聚類算法對樣本數據進行特徵提取,自適應的確定初始模糊規則和模糊神經網絡的初始結構參數,再結合最小二乘估計法和誤差反向傳播算法對模糊神經網絡的參數進行學習訓練。其中,聚類半徑是影響建模性能的關鍵參數,因此以預測精度為目標,利用PSO算法尋找聚類半徑的最優值。算法步驟如下:
4.1)利用Gamma Test算法尋找最優的模型輸入變量組合以及訓練樣本尺寸。Gamma Test算法是對所有光滑函數均適用的非參數估計方法,該方法不關注輸入輸出數據之間的任何參數關係,只對輸入輸出數據進行計算即可得到模型的噪聲方差,對於如下形式的數據集
{(Xi,Yi),1≤i≤m} (2)
式中,X∈Rn表示輸入,對應的輸出標量為y∈R。
Gamma Test假定的模型關係是:
y=f(x1,…,xn)+r (3)
式中,f是一個光滑函數,r是一個表示數據噪聲的隨機量。不失一般性,可假定r的均值為0(否則可在f中加入常數項),方差為Var(y)。Gamma Test就是計算一個統計量Γ,用它來評價輸出量的方差,顯然,如果數據的關係符合光滑模型,並且沒有噪聲,這個方差是0。Γ的計算過程如下:
4.1.1)計算輸入數據的距離統計量。用xi表示第i個輸入數據,xN[i,k]表示輸入樣本的第k近鄰域點,計算如下統計量:
<![CDATA[ δ m ( k ) = 1 m Σ i = 1 m | x N i , k - x i | 2 , 1 ≤ i ≤ m , 1 ≤ k ≤ p - - - ( 4 ) ]]>
式中,|·|表示歐拉距離,p為最遠鄰近距離(nearest neighbor)。
4.1.2)計算輸出數據的距離統計量。用yi表示第i個輸出數據,yN[i,k]表示輸出樣本的第k近鄰域點,計算如下統計量:
<![CDATA[ γ m ( k ) = 1 m Σ i = 1 m | y N i , k - y i | 2 , 1 ≤ i ≤ m , 1 ≤ k ≤ p - - - ( 5 ) ]]>
式中符號的意義同(4)式。
4.1.3)計算統計量Γ。為了計算Γ,分別計算鄰近距離從1到p的統計量(δm(1),γm(1)),(δm(2),γm(2)),…,(δm(p),γm(p))。對這p個統計量構造一元線性回歸模型,用最小二乘法進行擬合,得到的一次線性函數的截距就是Gamma Test統計量Γ,Γ值越小表示樣本中的噪聲越小。
定義另一個統計量Vratio:
式中,δ2(y)表示輸出y的方差。Vratio可以用來評價光滑模型對該數據的模擬能力,Vratio越接近0,表示該模型的預測性能越好。
本實施例中將p設置為10,訓練樣本的初始個數為2000。首先,確定最優的訓練樣本尺寸。分別計算當樣本尺寸分別是10~2000時,訓練樣本的Gamma Test統計量Γ,當Γ值趨於穩定時,得到的樣本尺寸就是最優的訓練樣本尺寸。其次,確定最優的模型輸入變量組合。需要計算所有輸入變量組合時的Γ值和Vratio值,選擇Γ值和Vratio值都很小的組合作為模型的最終輸入變量。
4.2)利用PSO算法尋找最優的聚類半徑。以聚類半徑rα作為粒子,15個粒子作為一個種群,每個粒子隨機賦予[0.20.9]區間內的隨機值,其中第i個粒子的位置的向量標示為ri,i=1,2,…,15;
4.3)以ri為聚類半徑,進行減法聚類分析。減法聚類算法用於對建模數據樣本的空間進行初始劃分以及模糊規則的確定,K-均值聚類算法和模糊C-均值聚類算法均需預設聚類中心的數目,沒有充分利用樣本空間的蘊含的對象特徵信息。而減法聚類算法是一種基於山峰函數的聚類算法,它將每個數據點作為可能的聚類中心,並根據各個數據點周圍的數據點密度來計算該點作為聚類中心的可能性。
每個數據點Xi作為聚類中心的可能性Pi由式(7)來定義:
式中m表示n維輸入空間中全部的數據點數,Xi=[Xi1,Xi2,...,Xin]、Xj=[Xj1,Xj2,...,Xjn]是具體的數據點,ri是一個正數,定義了該點的鄰域半徑,||·||符號表示歐式距離。被選為聚類中心的點具有最高的數據點密度,同時該該數據點周圍的點被排除作為聚類中心的可能性。第一個聚類中心為XC1,數據點密度為Pc1。選出第一個聚類中心後,繼續採用類似的方法確定下一個聚類中心,但需消除已有聚類中心的影響,修改密度指標的山峰函數如下:
其中,rβ定義了一個密度指標顯著減小的鄰域,為了避免出現十分接近的聚類中心,rβ=1.5ri。循環重複上述過程直到所有剩餘數據點作為聚類中心的可能性低於某一閾值δ,即Pck/Pc1<δ。
4.4)ANFIS模型訓練。不失一般性,假定減法聚類算法得到兩個聚類中心和得到兩條模糊規則:
Rule 1:
Rule 2:
ANFIS系統的第一層為系統的輸入層,由n個節點組成,它的作用是將輸入向量按原值傳遞到下一層。
第二層為模糊化層,由2n個節點組成,它的作用是計算各輸入分量屬於各語言變量值模糊集合的隸屬函數該層採用高斯函數進行模糊化處理,每個節點的輸出:
式中,cij和σij分別表示隸屬函數的中心和寬度。
第四層為歸一化層,節點數與第三層一樣,它所實現的是歸一化計算,即
<![CDATA[ w j = w j w 1 + w 2 , j = 1 , 2 - - - ( 10 ) ]]>
第五層為結論層,該層與第三層的節點數相同。其節點輸出為
<![CDATA[ O 4 i = w i f i = w i ( r i + p i 1 X 1 * + p i 2 X 1 * + ... + p i n X n * ) , i = 1 , 2 - - - ( 11 ) ]]>
第六層為輸出層及去模糊化層,只有一個節點,使用面積中心法進行解模糊,得到網絡的最終輸出為
對於模糊神經網絡模型的所有參數,採用混合最小二乘法的梯度下降算法進行學習,步驟如下:
4.4.1)在固定高斯型隸屬函數的中心和寬度的前提下,利用最小二乘法計算線性結論參數{r,p};
4.4.2)固定結論參數,採用誤差反向傳播算法對高斯函數的中心和寬度進行學習可得:
ΔS(t)=S(t+1)-S(t) (14)
式中S為參數c和σ,ηs為學習率,α為動量項,f為預測輸出,f*為實際輸出,E為平方誤差和,n為迭代步數。利用訓練樣本數據,重複上述步驟,直到滿足誤差指標或者達到最大訓練次數。
4.5)計算適應度值。利用訓練得到的預測模型計算垃圾熱值將床溫預測值與實際測量值y*進行比較,並以誤差平方和作為粒子的適應度值MSE,適應度計算公式如下:
4.6)更新極值。以適應度值為評價指標,比較當代粒子與上一代粒子之間的適應度值大小,如果當前粒子的適應度值優於上一代,則將當前粒子的位置設置為個體極值,否則個體極值保持不變。同時獲取當代所有粒子適應度值最優的粒子,並與上一代最優粒子進行比較,如果當代最優粒子的適應度值優於上一代最優粒子的適應度值,則將當代粒子的最優適應度值設置為全局最優值,否則全局最優值保持不變。
4.7)更新粒子。根據最新的個體極值和全局極值,按照(17)式和(18)式更新粒子的速度vid(t)和位置xid(t)。
vid(t+1)=ωvid(t)+c1r1(pid-xid(t))+c2r2(pgd-xid(t)) (17)
xid(t+1)=xid(t)+vid(t+1) (18)
t是粒子群優化算法的尋優代數。更進一步,為了改善基本粒子群算法容易陷入局部極值和收斂速度慢的缺陷,在PSO算法的基礎上引進了動態加速常數c1、c2和慣性權重ω:
其中,Tmax為最大尋優代數,ωmax為最大慣性權重,ωmin為最小慣性權重,R1、R2、R3、R4為常數。
4.8)算法停止條件算法判定。判斷是否達到最大迭代次數或者到達預測精度的要求,如果沒有達到則返回步驟4.3),利用更新的聚類半徑繼續搜索,否則退出搜索。
4.9)利用最終尋優得到的聚類半徑,對樣本進行聚類分析和ANFIS模型訓練,得到滿足訓練終止條件的ANFIS模型,即床溫預測模型。
5)預測床溫。對指定的樣本進行床溫預測,或者對當前鍋爐運行工況下的床溫進行實時預測。
實施例2
參照圖1、圖2、圖3、圖4,本發明提供的一種循環流化床生活垃圾焚燒鍋爐床溫預測系統,包括循環流化床生活垃圾焚燒鍋爐,用於該鍋爐運行控制的集散控制系統,數據通訊接口,資料庫以及上位機。資料庫通過數據通訊接口從集散控制系統中讀取數據,並用於上位機的訓練學習和測試,上位機通過數據通訊接口與集散控制系統進行數據交換,所述的上位機包括離線學習、驗證部分和在線床溫預測部分。具體包括:
第一信號採集模塊。利用該模型採集CFB生活垃圾焚燒鍋爐在正常運行時的運行工況狀態參數和操作變量,並組成ANIFS床溫預測模型輸入變量的訓練樣本矩陣X(m×n),和輸出訓練樣本矩陣Y(m×1),m表示樣本個數,n表示變量的個數。
數據預處理模塊。對訓練樣本進行粗大誤差處理和隨機誤差處理,剔除訓練樣本中的野值,排除異常工況,將訓練樣本輸入變量經歸一化處理後映射到[0,1]區間內,得到標準化後的訓練樣本X*(m×n)和Y*(m×1)。預處理過程採用以下步驟進行:
1.1)根據拉伊達準則,剔除訓練樣本X(m×n)和Y(m×1)中的野值;
1.2)剔除鍋爐停爐運行工況,鍋爐停爐時爐膛給煤機和給料機的開度為零,並且爐膛中溫度接近常溫;
1.3)剔除爐膛壓火運行狀況,鍋爐壓火時一次風機、二次風機引風機爐膛給煤機和給料機的開度為零,但是爐膛密相區的溫度維持在350℃~450℃;
1.4)剔除給料機堵塞工況,給料機堵塞需要運行人員通過給料口的攝像頭拍攝的畫面對給料情況進行判斷,給料機堵塞時,運行人員會顯著地調高給料機的開度,反映在運行數據上,即給料機的開度大於35%;
1.5)數據歸一化處理。按照式(1)將數據變量映射到[0 1]的區間內。
式中XJ表示第J變量所組成的向量,min表示最小值,max表示最大值。
專家知識庫模塊。將X*和Y*共同組成ANFIS床溫預測模型的訓練樣本,並進行保存。
智能學習模塊。智能學習模塊是床溫預測系統的核心部分,該模塊先利用Gamma Test算法尋找最優的模型輸入變量組合以及訓練樣本尺寸,然後採用減法聚類算法對樣本數據進行特徵提取,自適應的確定初始模糊規則和模糊神經網絡的初始結構參數,再結合最小二乘估計法和誤差反向傳播算法對模糊神經網絡的參數進行學習訓練。其中,聚類半徑是影響建模性能的關鍵參數,因此以預測精度為目標,利用PSO算法尋找聚類半徑的最優值。算法步驟如下:
2.1)利用Gamma Test算法尋找最優的模型輸入變量組合以及訓練樣本尺寸。Gamma Test算法是對所有光滑函數均適用的非參數估計方法,該方法不關注輸入輸出數據之間的任何參數關係,只對輸入輸出數據進行計算即可得到模型的噪聲方差,對於如下形式的數據集
{(Xi,Yi),1≤i≤m} (2)
式中,X∈Rn表示輸入,對應的輸出標量為y∈R。
Gamma Test假定的模型關係是:
y=f(x1,…,xn)+r (3)
式中,f是一個光滑函數,r是一個表示數據噪聲的隨機量。不失一般性,可假定r的均值為0(否則可在f中加入常數項),方差為Var(y)。Gamma Test就是計算一個統計量Γ,用它來評價輸出量的方差,顯然,如果數據的關係符合光滑模型,並且沒有噪聲,這個方差是0。Γ的計算過程如下:
2.1.1)計算輸入數據的距離統計量。用xi表示第i個輸入數據,xN[i,k]表示輸入樣本的第k近鄰域點,計算如下統計量:
<![CDATA[ δ m ( k ) = 1 m Σ i = 1 m | x N i , k - x i | 2 , 1 ≤ i ≤ m , 1 ≤ k ≤ p - - - ( 4 ) ]]>
式中,|·|表示歐拉距離,p為最遠鄰近距離(nearest neighbor)。
2.1.2)計算輸出數據的距離統計量。用yi表示第i個輸出數據,yN[i,k]表示輸出樣本的第k近鄰域點,計算如下統計量:
<![CDATA[ γ m ( k ) = 1 m Σ i = 1 m | y N i , k - y i | 2 , 1 ≤ i ≤ m , 1 ≤ k ≤ p - - - ( 5 ) ]]>
式中符號的意義同(4)式。
2.1.3)計算統計量Γ。為了計算Γ,分別計算鄰近距離從1到p的統計量(δm(1),γm(1)),(δm(2),γm(2)),…,(δm(p),γm(p))。對這p個統計量構造一元線性回歸模型,用最小二乘法進行擬合,得到的一次線性函數的截距就是Gamma Test統計量Γ,Γ值越小表示樣本中的噪聲越小。
定義另一個統計量Vratio:
式中,δ2(y)表示輸出y的方差。Vratio可以用來評價光滑模型對該數據的模擬能力,Vratio越接近0,表示該模型的預測性能越好。
本實施例中將p設置為10,訓練樣本的初始個數為2000。首先,確定最優的訓練樣本尺寸。分別計算當樣本尺寸分別是10~2000時,訓練樣本的Gamma Test統計量Γ,當Γ值趨於穩定時,得到的樣本尺寸就是最優的訓練樣本尺寸。其次,確定最優的模型輸入變量組合。需要計算所有輸入變量組合時的Γ值和Vratio值,選擇Γ值和Vratio值都很小的組合作為模型的最終輸入變量。
2.2)利用PSO算法尋找最優的聚類半徑。以聚類半徑rα作為粒子,15個粒子作為一個種群,每個粒子隨機賦予[0.20.9]區間內的隨機值,其中第i個粒子的位置的向量標示為ri,i=1,2,…,15;
2.3)以ri為聚類半徑,進行減法聚類分析。減法聚類算法用於對建模數據樣本的空間進行初始劃分以及模糊規則的確定,K-均值聚類算法和模糊C-均值聚類算法均需預設聚類中心的數目,沒有充分利用樣本空間的蘊含的對象特徵信息。而減法聚類算法是一種基於山峰函數的聚類算法,它將每個數據點作為可能的聚類中心,並根據各個數據點周圍的數據點密度來計算該點作為聚類中心的可能性。
每個數據點Xi作為聚類中心的可能性Pi由式(7)來定義:
式中m表示n維輸入空間中全部的數據點數,Xi=[Xi1,Xi2,...,Xin]、Xj=[Xj1,Xj2,...,Xjn]是具體的數據點,ri是一個正數,定義了該點的鄰域半徑,||·||符號表示歐式距離。被選為聚類中心的點具有最高的數據點密度,同時該該數據點周圍的點被排除作為聚類中心的可能性。第一個聚類中心為XC1,數據點密度為Pc1。選出第一個聚類中心後,繼續採用類似的方法確定下一個聚類中心,但需消除已有聚類中心的影響,修改密度指標的山峰函數如下:
其中,rβ定義了一個密度指標顯著減小的鄰域,為了避免出現十分接近的聚類中心,rβ=1.5ri。循環重複上述過程直到所有剩餘數據點作為聚類中心的可能性低於某一閾值δ,即Pck/Pc1<δ。
2.4)ANFIS模型訓練。不失一般性,假定減法聚類算法得到兩個聚類中心和得到兩條模糊規則:
Rule 1:
Rule 2:
ANFIS系統的第一層為系統的輸入層,由n個節點組成,它的作用是將輸入向量按原值傳遞到下一層。
第二層為模糊化層,由2n個節點組成,它的作用是計算各輸入分量屬於各語言變量值模糊集合的隸屬函數該層採用高斯函數進行模糊化處理,每個節點的輸出:
式中,cij和σij分別表示隸屬函數的中心和寬度。
第四層為歸一化層,節點數與第三層一樣,它所實現的是歸一化計算,即
<![CDATA[ w j = w j w 1 + w 2 , j = 1 , 2 - - - ( 10 ) ]]>
第五層為結論層,該層與第三層的節點數相同。其節點輸出為
<![CDATA[ O 4 i = w i f i = w i ( r i + p i 1 X 1 * + p i 2 X 1 * + ... + p i n X n * ) , i = 1 , 2 - - - ( 11 ) ]]>
第六層為輸出層及去模糊化層,只有一個節點,使用面積中心法進行解模糊,得到網絡的最終輸出為
對於模糊神經網絡模型的所有參數,採用混合最小二乘法的梯度下降算法進行學習,步驟如下:
2.4.1)在固定高斯型隸屬函數的中心和寬度的前提下,利用最小二乘法計算線性結論參數{r,p};
2.4.2)固定結論參數,採用誤差反向傳播算法對高斯函數的中心和寬度進行學習可得:
ΔS(t)=S(t+1)-S(t) (14)
式中S為參數c和σ,ηs為學習率,α為動量項,f為預測輸出,f*為實際輸出,E為平方誤差和,n為迭代步數。利用訓練樣本數據,重複上述步驟,直到滿足誤差指標或者達到最大訓練次數。
2.5)計算適應度值。利用訓練得到的預測模型計算垃圾熱值將床溫預測值與實際測量值y*進行比較,並以誤差平方和作為粒子的適應度值MSE,適應度計算公式如下:
2.6)更新極值。以適應度值為評價指標,比較當代粒子與上一代粒子之間的適應度值大小,如果當前粒子的適應度值優於上一代,則將當前粒子的位置設置為個體極值,否則個體極值保持不變。同時獲取當代所有粒子適應度值最優的粒子,並與上一代最優粒子進行比較,如果當代最優粒子的適應度值優於上一代最優粒子的適應度值,則將當代粒子的最優適應度值設置為全局最優值,否則全局最優值保持不變。
2.7)更新粒子。根據最新的個體極值和全局極值,按照(17)式和(18)式更新粒子的速度vid(t)和位置xid(t)。
vid(t+1)=ωvid(t)+c1r1(pid-xid(t))+c2r2(pgd-xid(t)) (17)
xid(t+1)=xid(t)+vid(t+1) (18)
t是粒子群優化算法的尋優代數。更進一步,為了改善基本粒子群算法容易陷入局部極值和收斂速度慢的缺陷,在PSO算法的基礎上引進了動態加速常數c1、c2和慣性權重ω:
其中,Tmax為最大尋優代數,ωmax為最大慣性權重,ωmin為最小慣性權重,R1、R2、R3、R4為常數。
2.8)算法停止條件算法判定。判斷是否達到最大迭代次數或者到達預測精度的要求,如果沒有達到則返回步驟4.3),利用更新的聚類半徑繼續搜索,否則退出搜索。
2.9)利用最終尋優得到的聚類半徑,對樣本進行聚類分析和ANFIS模型訓練,得到滿足訓練終止條件的ANFIS模型,即床溫預測模型。
第二信號採集模塊。用於從資料庫中選擇需要預測床溫的運行工況,或者實時地採集當前鍋爐的運行工況。
預測模塊。該模塊用於對指定的樣本進行床溫預測,或者對當前鍋爐運行工況下的床溫進行實時預測。
結果顯示模塊。顯示床溫的預測結果,或者對床溫的預測結果進行統計分析。
本發明所提出的循環流化床鍋爐入爐垃圾熱值預測系統及方法,已通過上述具體實施步驟進行了描述,相關技術人員明顯能在不脫離本發明內容、精神和範圍內對本文所述的裝置和操作方法進行改動或適當變更與組合,來實現本發明技術。特別需要指出的是,所有相類似的替換和改動對本領域的技術人員是顯而易見的,它們都會被視為包括在本發明精神、範圍和內容中。
