最小間距可控的超寬帶無柵瓣稀疏線陣設計方法與流程
2023-12-09 05:38:51
本發明涉及天線,尤其是涉及一種最小間距可控的超寬帶無柵瓣稀疏線陣設計方法。
背景技術:
隨著電子技術的飛速發展和寬帶通信設備的出現,天線的超寬帶技術也在不斷發展。超寬帶天線可以實現寬帶信號的瞬時接收,且可以為不同功能系統共享使用,在通信、導航、雷達中具有較為廣泛的應用[1,2]。在不同應用下超寬帶有不同的定義,本發明中對超寬帶的定義指的是頻域的帶寬比值不小於3︰1。稀疏陣列是指陣元位置不再以半波長等間距均勻分布,而是按照某種規則進行不等間距分布,其具有波束窄、空間角解析度高、能減弱陣元間互耦等特點,這些優點使得稀疏陣列天線頗具實用性,在雷達、聲納系統等中具有重要作用[3]。眾所周知,按照傳統方法設計等間隔超寬帶陣列時,頻率增大時電尺寸也會不斷增大,最終導致在高頻段時產生柵瓣問題[4,5];而如果採用稀疏陣列布局技術,則可以在一定程度上降低柵瓣電平。由於實際工程中的單元天線總是具有一定的物理尺寸,因此稀疏陣列設計通常需滿足最小間距的設計要求。
關於稀疏陣列的研究有很多,文獻[6]中提出了一種基於凸優化實現陣列稀疏化的方法,兩個優化目標分別是最大程度降低峰值副瓣電平和最大化稀疏度,相對於陣元數目相同的均勻線陣,該稀疏線陣具有更低的峰值副瓣電平和更窄的主瓣寬度,但該方法並未涉及到寬帶的性能。中國專利CN201410419309.4公開了一種陣列天線輻射場和散射場綜合低副瓣快速實現方法[7],該專利先對均勻陣列優化得到初始稀疏排布方案,再計算和對比陣列天線的輻射場和散射場的最大副瓣電平,當同時滿足低副瓣要求則得到優化結果,否則通過交叉和變異的方法更新陣列天線稀疏排布矩陣,該專利不足之處在於並未涉及到寬帶性能,該陣列在超寬帶頻率範圍工作時存在出現柵瓣的問題。另外,中國專利CN201510770122.3公開了一種基於地理空間約束的稀疏天線陣列的優化布陣方法[3],控制了最小間距,但同樣也沒有實現超寬帶性能,其柵瓣/副瓣區域峰值電平也較高。
稀疏陣列設計方法提供了實現期望副瓣電平的可能性,但更多是在窄帶範圍內布局,對副瓣及柵瓣電平的抑制也較弱。在[8]中,均勻激勵的陣元隨機分布在指定的孔徑上,該方法不能保證陣元有足夠的間距或者嚴格滿足旁瓣電平的要求。在[9]中研究了在有限帶寬上使用多個給定方向圖的小陣列來合成所需的陣列以及方向圖。後來,基於分形概念已經設計出多頻帶陣列以及對帶寬相當不敏感但旁瓣電平抑制能力有限的陣列配置[10-13]。還有一些陣列設計方法只能在窄帶或者有限掃描範圍內抑制副瓣電平和實現方向圖控制[14-17]。在[18]中使用了陣元數目相對較少(例如8或16個陣元)的掃描陣列,對陣元進行簡單擾動而得到優化。波束掃描可以被認為是增加帶寬;波束控制在可見區域操作陣因子,帶寬增加時陣因子被壓縮到可見區域;在窄帶陣列設計中,這兩個方法都可能導致柵瓣的出現[19,20]。
近年來,許多研究者開始嘗試在更寬的頻率範圍內合成無柵瓣/低副瓣寬帶陣列方向圖,許多全局優化方法得到較為廣泛的應用[21-24],但是對於大型的陣列天線綜合而言,全局優化法計算量偏大,收斂速度較慢。超寬帶線性、平面和體積陣列設計通過將優化方法與陣列表示技術相結合,例如分形、非周期分割和其他數學結構,這些方法使得所設計陣列的方向圖在很寬的頻率範圍內擁有很低的峰值副瓣電平,而且得到陣元數目少、窄波束、大帶寬和相對低的成本的大孔徑稀疏陣列。目前已經成功地使用分形技術[25-27]和升冪級數[28]來設計有效的超寬帶稀疏線性陣列,這些方法對於設計包含從一百到幾千個元素的線性陣列布局最有用。分形技術引入連接因子來控制分形發生器「樹」在迭代構建過程中如何相互應用,分形「樹」末端(分支的尖端)的幾何形狀決定了陣列布局。這種設計優化技術已經被證明,對於設計中型到非常大尺寸的超寬帶陣列是非常有效的,甚至可以多達數千個元件。在[28]中基於升冪級數表示的陣列非常類似於分形結構,其中不斷重複地用優化的子陣列替換原陣列中的元素以生成更大的陣列,解決了均勻線陣在高頻段產生柵瓣的問題,在帶寬很寬的工作波段內柵瓣/副瓣區域的峰值電平基本保持不變。但是該方法得到的最小間距大於低頻半波長的101元或以下超寬帶陣列的峰值副瓣/柵瓣電平僅為-10db左右,無法滿足通常工程應用的需求。因此,在此基礎上進一步優化陣元位置分布以降低陣列峰值副瓣/柵瓣電平,則顯得尤為重要。
參考文獻:
[1]張志亞.寬帶天線及波束賦形陣列天線研究[D].西安電子科技大學,2012.
[2]陳立甲等.超寬帶天線:中國,201510560304.8[P].2015-12-23.
[3]崔國龍等.一種基於地理約束的稀疏天線陣列的優化布陣方法:中國201510770122.3[P].2016-03-16.
[4]羅天光.大間距相控陣天線柵瓣抑制方法研究[D].電子科技大學,2014.
[5]潘敏.線形陣列柵瓣的抑制[J].大眾科技,2009(12):32-33.
[6]Cen L,Ser W,Cen W,et al.Linear sparse array synthesis via convex optimization[C]//Proceedings of 2010IEEE International Symposium on Circuits and Systems.IEEE,2010:4233-4236.
[7]王從思等.一種陣列天線輻射場和散射場綜合低副瓣快速實現方法:中國專利CN201410419309.4[P].2014-12-03.
[8]Lo Y.A mathematical theory of antenna arrays with randomly spaced elements[J].IEEE Transactions on Antennas and Propagation,1964,12(3):257-268.
[9]King D,Packard R,Thomas R.Unequally-spaced,broad-band antenna arrays[J].IEEE Transactions on Antennas and Propagation,1960,8(4):380-384.
[10]Kim Y,Jaggard D L.The fractal random array[C]//IEEE Proceedings.1986,74:1278-1280.
[11]Puente-Baliarda C,Pous R.Fractal design of multiband and low side-lobe arrays[J].IEEE Transactions on Antennas and Propagation,1996,44(5):730.
[12]Werner D H,Gingrich M A,Werner P L.A self-similar fractal radiation pattern synthesis technique for reconfigurable multiband arrays[J].IEEE Transactions on Antennas and Propagation,2003,51(7):1486-1498.
[13]Werner D H,Ganguly S.An overview of fractal antenna engineering research[J].IEEE Antennas and propagation Magazine,2003,45(1):38-57.
[14]Jin N,Rahmat-Samii Y.Advances in particle swarm optimization for antenna designs:Real-number,binary,single-objective and multiobjective implementations[J].IEEE Transactions on Antennas and Propagation,2007,55(3):556-567.
[15]Haupt R L.Thinned arrays using genetic algorithms[J].IEEE Transactions on Antennas and Propagation,1994,42(7):993-999.
[16]Weile D S,Michielssen E.Integer coded Pareto genetic algorithm design of constrained antenna arrays[J].Electronics Letters,1996,32(19):1744-1745.
[17]Ares-Pena F J,Rodriguez-Gonzalez J A,Villanueva-Lopez E,et al.Genetic algorithms in the design and optimization of antenna array patterns[J].IEEE Transactions on Antennas and Propagation,1999,47(3):506-510.
[18]Bray M G,Werner D H,Boeringer D W,et al.Optimization of thinned aperiodic linear phased arrays using genetic algorithms to reduce grating lobes during scanning[J].IEEE Transactions on antennas and propagation,2002,50(12):1732-1742.
[19]Petko J S,Werner D H.The pareto optimization of ultrawideband polyfractal arrays[J].IEEE Transactions on Antennas and Propagation,2008,56(1):97-107.
[20]Doles J H,Benedict F D.Broad-band array design using the asymptotic theory of unequally spaced arrays[J].IEEE transactions on antennas and propagation,1988,36(1):27-33.
[21]Rocca P,Benedetti M,Donelli M,et al.Evolutionary optimization as applied to inverse scattering problems[J].Inverse Problems,2009,25(12):123003.
[22]Rocca P,Oliveri G,Massa A.Differential evolution as applied to electromagnetics[J].IEEE Antennas and Propagation Magazine,2011,53(1):38-49.
[23]Robinson J,Rahmat-Samii Y.Particle swarm optimization in electromagnetics[J].IEEE transactions on antennas and propagation,2004,52(2):397-407.
[24]Goudos S K,Siakavara K,Samaras T,et al.Self-adaptive differential evolution applied to real-valued antenna and microwave design problems[J].IEEE Transactions on Antennas and Propagation,2011,59(4):1286-1298.
[25]Petko J S,Werner D H.The evolution of optimal linear polyfractal arrays using genetic algorithms[J].IEEE transactions on antennas and propagation,2005,53(11):3604-3615.
[26]Petko J S,Werner D H.An autopolyploidy-based genetic algorithm for enhanced evolution of linear polyfractal arrays[J].IEEE transactions on antennas and propagation,2007,55(3):583-593.
[27]Petko J S,Werner D H.Interleaved ultrawideband antenna arrays based on optimized polyfractal tree structures[J].IEEE Transactions on Antennas and Propagation,2009,57(9):2622-2632.
[28]Gregory M D,Werner D H.Ultrawideband aperiodic antenna arrays based on optimized raised power series representations[J].IEEE Transactions on Antennas and Propagation,2010,58(3):756-764.
技術實現要素:
本發明的目的在於針對現有技術中存在的上述不足,提供最小間距可控的超寬帶無柵瓣稀疏線陣,而且有較低的峰值副瓣電平;在保證寬頻帶內柵瓣/副瓣區域的峰值電平基本保持不變的前提下,還可以最大程度降低柵瓣/副瓣區域的峰值電平;相對於一些算法如遺傳算法等,基於迭代凸優化的數值微擾優化法優化速度明顯加快的最小間距可控的超寬帶無柵瓣稀疏線陣設計方法。
本發明包括以下步驟:
1)假設在天線陣列的布陣範圍為[-D/2,D/2]上布置了2N+1個陣元,位置為d-N,d-(N-1),...,d0,d1,...,dN-1,dN,其中d-N=-D/2,dN=D/2,為陣列的孔徑大小,對於任何寬帶天線單元激勵等幅同相的陣列,當天線系統的工作波段在一倍頻至三倍頻(f0~3f0,對應的波長為)時,此波段內柵瓣/副瓣區域的峰值電平基本保持不變(誤差小於0.5dB)。具體步驟如下:
(1)對於一個沿Z軸均勻分布並且關於原點對稱的線陣,它的陣因子公式為
其中,β表示自由空間波數,d是陣元間距為表示求和運算符,θ表示從X軸觀測的角度,已知均勻陣列在高頻波段會生成柵瓣,為了抑制柵瓣生成,對陣元位置進行初步優化;
(2)將式(1)中的n變為nr,並引入一個新的參數ξ,該參數由式(2)確定,新的dn由式(3)給出,得到的新陣列為RPS陣,它的陣因子表達式為式(4):
dn=sign(n)dminξ|n|r,|n|≤N (3)
其中,dmin為λ0/2(低頻時的半個波長),選取合適的r和N,使得天線系統工作在波段f0~3f0時,柵瓣/副瓣區域的峰值電平基本保持不變。
2)為了進一步降低柵瓣/副瓣區域的峰值電平,採用多步數值微擾優化法。所述多步數值微擾優化法的具體步驟為:將式(4)中陣元位置dn(n=0,1,2,…N)變成dn+Δn,Δn代表每一個陣元的位置微擾量,由於這個約束條件,微擾後的陣因子式可以表達為式(5):
其中,AF(θ)是微擾前的陣因子式,是一步位置微擾後產生的變化量;
微擾時保證滿足最小間距約束、位置微擾幅度約束兩個條件,對以上線性陣列的陣元位置進行微擾,具體約束條件如下:
(1)最小間距約束:在實際天線陣布局過程中,陣元間距需不小於所設計的單元天線尺寸,因此在微擾過程中,需要滿足最小間距約束dn-dn-1≥dmin,dmin為λ0/2,n=0,1,2,…N;
(2)位置微擾幅度約束:為了保證位置微擾的近似精度,要求即對於n=0,1,2,…N,均滿足|βΔn|≤μ,此處的μ的大小決定了位置微擾的幅度;
遵循以上約束條件,採用迭代二階錐規劃法對RPS陣進行多步位置微擾優化,在每一步微擾,二階錐規劃法的優化目標是最小化柵瓣/副瓣區域的峰值電平;多步微擾後,當柵瓣/副瓣區域的峰值電平基本保持不變且陣列布局也保持不變時,得到最優化陣列布局結果。
本發明的基本思路是:首先,解析法設計超寬帶稀疏線陣;然後通過多步位置微擾,進一步優化解析法設計的RPS陣,使得柵瓣/副瓣區域的峰值電平大大降低。在整個優化布局的過程中,最小間距始終可控。
與現有技術相比,本發明的有益效果在於:解析法與數值法相結合,解決了稀疏陣列在寬頻帶波段工作時,會產生柵瓣以及較高峰值副瓣的問題,並最大程度的降低柵瓣/副瓣區域峰值電平;在至少三倍頻的波段範圍內柵瓣/副瓣區域峰值電平基本保持不變,在整個過程中最小間距可控。
附圖說明
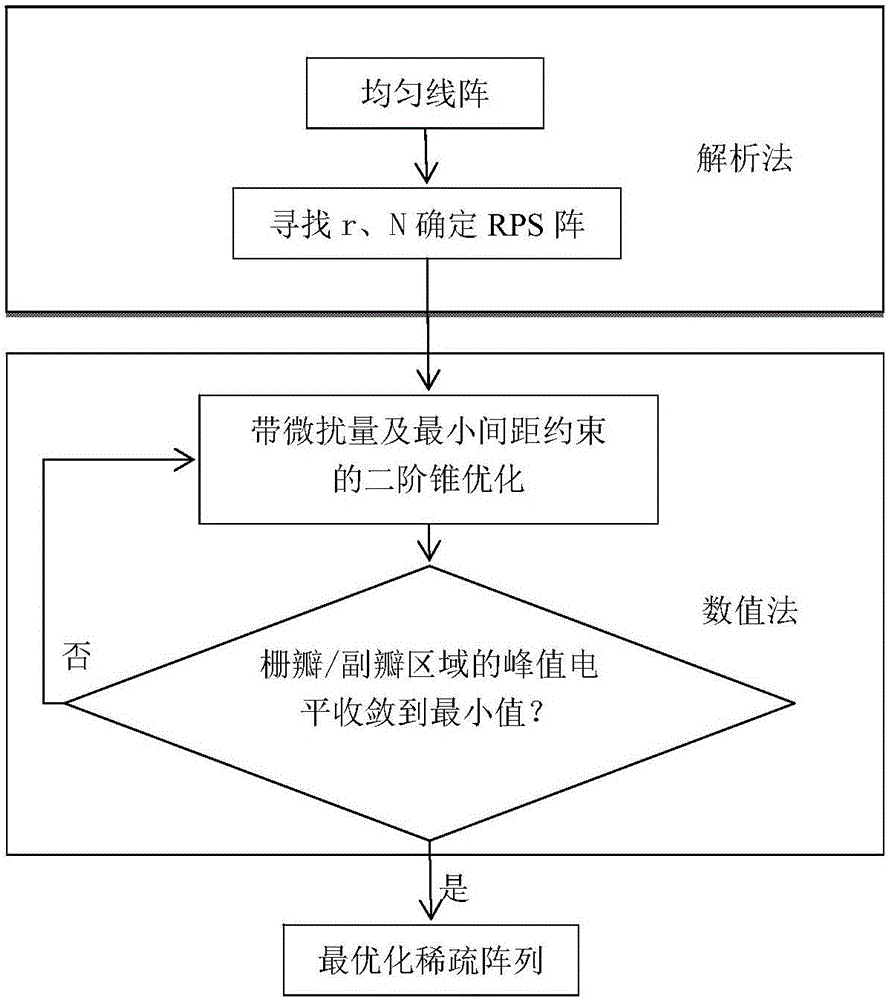
圖1為本發明的技術方案流程圖。
圖2為不同r、N值下的柵瓣/峰值副瓣電平。
圖3為初始RPS陣在3GHz時的陣因子圖。
圖4為最優化稀疏陣列在3GHz時的陣因子圖。
圖5為優化布局過程中的峰值副瓣電平圖。
圖6為優化布局過程中正半軸的陣元位置圖mark。
圖7為最優化稀疏陣列頻率1GHz下的陣因子圖。
圖8為最優化稀疏陣列頻率1.5GHz下的陣因子圖。
圖9為最優化稀疏陣列頻率2GHz下的陣因子圖。
圖10為最優化稀疏陣列頻率2.5GHz下的陣因子圖。
圖11為最優化稀疏陣列頻率3GHz下的陣因子圖。
具體實施方式
本發明提出的最小間距可控的超寬帶無柵瓣稀疏線陣設計方法分為兩步,如圖1所示:第一步,解析法設計的RPS陣,確定了超寬帶稀疏線陣;第二步,多步數值微擾優化上述陣列的陣元位置得到更低柵瓣/峰值副瓣電平的最小間距可控的超寬帶稀疏線陣。圖1為本發明的技術流程圖。
下面結合一個實例對本發明做進一步解釋。設計目標:頻率範圍在1GHz~3GHz之間,柵瓣/副瓣區域的峰值電平保持不變的超寬帶無柵瓣稀疏線陣。
按下面步驟實施:
步驟1:假設在天線陣列的布陣範圍為上布置了個激勵等幅同相的寬帶天線陣元,位置為d-N,d-(N-1),...,d0,d1,...,dN-1,dN,其中d-N=-D/2,dN=D/2。
步驟1-1:對於一個均勻分布的周期線陣,在笛卡爾坐標系中,2N+1個陣元沿Z軸關於原點對稱分布,此周期陣列的陣因子冪級數表達式為
其中,從X軸觀測的角度θ為[0°,90°],採樣密度Δθ是0.02°,陣元間距d為0.15m(低頻(1GHz)時的半個波長),β是自由空間的波數。已知均勻陣列在高頻波段會生成柵瓣,為了抑制柵瓣,下一步將對上述陣列進行初步優化。
步驟1-2:將式(6)中的變為nr,並引入一個新的參數ξ,該參數由式(7)確定,新的dn由式(8)給出,得到RPS陣,它的陣因子表達式為式(9)。
dn=sign(n)dminξ|n|r,|n|≤N (8)
其中,dmin為0.15m(低頻(1GHz)時的半個波長)。為了避免過度稀疏化,r值不可選取的過大或過小,因此0.75≤r≤1.25。為了選取合適的r、N值,由圖2得知,當r取0.81、N取50時,柵瓣/峰值副瓣電平在三倍頻的頻率範圍內基本保持不變,因此我們得到了解析法解出的超寬帶無柵瓣線陣。在圖3中,讀出此時的峰值副瓣電平為-9.4263dB。
步驟2:在高頻3GHz時,採用多步數值微擾優化法對陣元位置微擾來進一步降低柵瓣/副瓣區域的峰值電平。將式(9)中陣元位置dn(n=0,1,2,…N)變成dn+Δn,Δn代表每一個陣元的位置微擾量,為了保證位置微擾的近似精度有微擾後的陣因子式可以表達為式(10):
其中,AF(θ)是微擾前的陣因子式,是一步位置微擾後產生的變化量。
微擾時保證滿足最小間距約束、位置微擾幅度約束兩個條件,對以上線性陣列的陣元位置進行微擾,具體約束條件如下:
(1)最小間距約束:在實際天線陣布局過程中,陣元間距需不小於所設計的單元天線尺寸,因此在微擾過程中,需要滿足最小間距約束dn-dn-1≥dmin,dmin為λ0/2,n=0,1,2,…N。
(2)位置微擾幅度約束:為了保證位置微擾的近似精度,要求即對於n=0,1,2,…N,均滿足|βΔn|≤μ,此處的μ的大小決定了位置微擾的幅度。本例中μ為π/5,相對於工作波長位置微擾為1/10。
遵循以上約束條件,採用迭代二階錐規劃法對RPS陣進行多步位置微擾優化。在每一步微擾,二階錐規劃法的優化目標是最小化柵瓣/副瓣區域的峰值電平。多步微擾後,當柵瓣/副瓣區域的峰值電平基本保持不變且陣列布局也保持不變時,得到最優化陣列布局結果。圖4是最終優化稀疏陣列在3GHz時的陣因子圖,此時的柵瓣/副瓣區域的峰值電平為-14.6514dB。本例中柵瓣/副瓣區域的峰值電平總共降低了5.2251dB。
圖5給出了每步微擾結果的柵瓣/副瓣區域的峰值電平值,大約100次迭代後,柵瓣/副瓣區域的峰值電平降到大約-14.6514dB,隨後基本保持不變。圖6給出了優化布局過程中部分次陣元位置布局圖,由於陣元關於原點對稱分布,這裡僅畫出正半軸的陣元。可以看出多步微擾後,陣列布局保持不變。圖7~11給出了5個不同頻率(1GHz、1.5GHz、2GHz、2.5GHz和3GHz)下的陣因子圖,它們的柵瓣/副瓣區域的峰值電平分別為-14.65dB、-14.63dB、-14.65dB、-14.65dB、-14.65dB,在誤差不超過0.5dB時,該結果可以認定為基本保持不變。
