雙Buck全橋逆變器迭代學習控制方法與流程
2024-03-07 04:02:15 2
本發明屬於逆變器建模與控制技術領域,具體地說,涉及一種雙buck全橋逆變器迭代學習控制方法。
背景技術:
逆變技術通過功率開關器件將直流電能變換為交流電能,其在新能源發電、不間斷電源、調速系統等領域具有至關重要的地位。然而傳統橋式逆變器由於開關管的體二極體性能差,導致很大損耗並限制了開關頻率的提高。而雙buck逆變電路功率開關管和功率二極體可以分別得到最優設計,該變換器同時克服了傳統橋式逆變器的直通問題,且電壓利用率高。
然而,由於輸入直流電源波動、死區效應、穩態時線性和非線性負載電流的擾動會引起逆變器周期性擾動,使輸出波形發散畸變。會對逆變器上的其他設備造成影響、無法正常工作,嚴重時會導致其損壞。因此在主電路拓撲固定的情況下,提出一種合適的控制策略解決周期性擾動問題十分必要。
技術實現要素:
本發明的目的在於提供一種雙buck全橋逆變器迭代學習控制方法,該方法可確保雙buck全橋逆變器有較好的負載適應能力和優越的跟蹤性能。
為實現上述目的,本發明的技術方案是:一種雙buck全橋逆變器迭代學習控制方法,針對逆變器在直流電源波動、死區效應、穩態時線性和非線性負載電流擾動產生的周期性擾動,採用電壓外環迭代學習控制+電流內環無差拍控制的雙環控制策略,提高雙buck逆變器的輸出效率,使系統輸出電壓能精確跟蹤參考信號,並增強系統穩定性和提高動態響應性能。
在本發明一實施例中,該方法具體實現步驟如下,
根據基爾霍夫電壓和電流定律,由於濾波電感l1、l2的電流il1(t)=il2(t),可令il1(t)=il2(t)=il(t),且令電感量l1=l2=l,由於逆變器正負半周對稱,因此此處僅分析正半周,可令ua(t)=u(t),得逆變器系統模型如下:
其中,c為濾波電容的電容值;
選擇電容電壓uc和電感電流il為狀態變量,逆變器交流輸出電壓u(t)和負載電流ir(t)為輸入,電容電壓uc為系統輸出;於是,x(t)=[uc(t),il(t)],u(t)=[u(t),ir(t)],y(t)=uc(t);逆變器系統狀態方程為:
其中,c=(10)
由於直流電源波動、死區效應、穩態時線性和非線性負載電流擾動引起的周期性擾動,對應的逆變器系統狀態方程可寫為:
其中,w(t),v(t)為周期性擾動;為解決該周期性擾動,採用電壓外環迭代學習控制+電流內環無差拍控制的雙環控制策略,具體策略如下:
設負載參考電壓為yd(t),負載採樣電壓為yk(t),可得輸出誤差為:ek(t)=yd(t)-yk(t),採用迭代學習控制開閉環p型學習律進行迭代,對應學習律公式如下:
uk+1(t)=uk(t)+γ1(t)ek(t)+γ2(t)ek+1(t)
得迭代學習控制算法流程如下:
(1)初始時,設負載參考電壓為yd(t),初始控制量為u0(t),時間間隔為t∈[0,t];
(2)系統的初始輸出量為yk(0),初始狀態量為xk(0);
(3)使控制輸入量uk(t)輸入到被控系統中,得系統輸出量為yk(t),重複操作;
(4)在時間間隔t∈[0,t]內負載採樣電壓與參考電壓的誤差為ek(t)=yd(t)-yk(t);採用上式學習律公式計算,得新的控制輸入量為uk+1(t);
(5)判斷,迭代是否滿足了停止條件(預設的迭代次數),如果滿足就停止;否則,令k=k+1,轉到步驟(2),繼續運行;
經若干次迭代後,使得yk(t)→yd(t);
迭代學習控制開閉環p型學習律若滿足||i-γ1(t)d(t)||·||[i+γ2(t)d(t)]-1||<1,則控制律收斂;由此可計算出γ1(t)、γ2(t)的值;
由於迭代學習控制動態性能較差,對此採樣兩電感電流作為內環控制,由於電流比電壓有更快的響應速度,系統的許多變化都會第一時間在電流上有所表現,所以內環電流控制能起到增強系統穩定性和提高動態響應性能的能力。
相較於現有技術,本發明具有以下有益效果:本發明採用新型器件sicmosfet,提出了電壓外環迭代學習控制+電流內環無差拍控制的雙環控制策略不僅保留了雙buck全橋逆變器無橋臂直通問題,提高雙buck逆變器的輸出效率,電壓利用率高,且解決了直流電源波動、死區效應、穩態時線性和非線性負載電流擾動引起的周期性擾動問題。
附圖說明
圖1為雙buck全橋逆變器主電路拓撲圖。
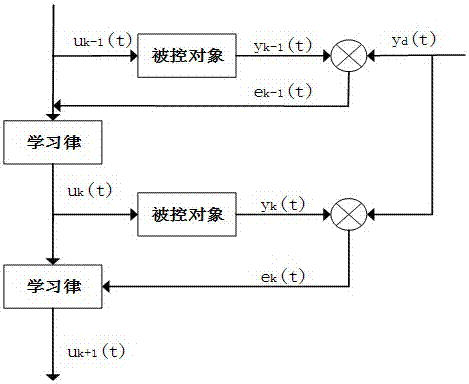
圖2為迭代學習控制算法流程圖。
圖3為傳統雙環pid控制輸出電壓仿真波形圖。
圖4為迭代學習控制下輸出電壓仿真波形圖。
圖5為迭代學習控制下參考和實際輸出電壓仿真波形圖。
圖6為加周期性擾動後傳統雙環pid控制輸出電壓仿真波形圖。
圖7為迭代學習控制下加周期性擾動後參考與實際輸出電壓波形圖。
具體實施方式
下面結合附圖1-7,對本發明的技術方案進行具體說明。
本發明的一種雙buck全橋逆變器迭代學習控制方法,針對逆變器在直流電源波動、死區效應、穩態時線性和非線性負載電流擾動產生的周期性擾動,採用電壓外環迭代學習控制+電流內環無差拍控制的雙環控制策略,使系統輸出電壓能精確跟蹤參考信號,提高雙buck逆變器的輸出效率,並增強系統穩定性和提高動態響應性能;該方法具體實現步驟如下,
根據基爾霍夫電壓和電流定律,由於濾波電感l1與l2的電流il1(t)=il2(t),可令il1(t)=il2(t)=il(t),且令電感量l1=l2=l,濾波電容c,由於逆變器正負半周對稱,因此這裡只分析正半周,可令ua(t)=u(t),得逆變器系統模型如下:
選擇電容電壓uc和電感電流il為狀態變量,逆變器交流輸出電壓u(t)和負載電流ir(t)為輸入,電容電壓uc為系統輸出;於是,x(t)=[uc(t),il(t)],u(t)=[u(t),ir(t)],y(t)=uc(t);逆變器系統狀態方程為:
其中,c=(10)
由於直流電源波動、死區效應、穩態時線性和非線性負載電流擾動引起的周期性擾動,對應的逆變器系統狀態方程可寫為:
其中,w(t),v(t)為周期性擾動;為解決該周期性擾動,採用電壓外環迭代學習控制+電流內環無差拍控制的雙環控制策略,具體策略如下:
設負載參考電壓為yd(t),負載採樣電壓為yk(t),可得輸出誤差為:ek(t)=yd(t)-yk(t),採用迭代學習控制開閉環p型學習律進行迭代,對應學習律公式如下:
uk+1(t)=uk(t)+γ1(t)ek(t)+γ2(t)ek+1(t)
得迭代學習控制算法流程如下:
(1)初始時,設負載參考電壓為yd(t),初始控制量為u0(t),時間間隔為(t∈[0,t])。
(2)系統的初始輸出量為yk(0),初始狀態量為xk(0)。
(3)使控制輸入量uk(t)(t∈[0,t])輸入到被控系統中,得系統輸出量為yk(t)(t∈[0,t])。重複操作。
(4)在一定時間間隔(t∈[0,t])內負載採樣電壓與參考電壓的誤差為ek(t)=yd(t)-yk(t)。採用上式迭代學習律計算,得新的控制輸入量為(t∈[0,t])uk+1(t)。
(5)判斷,迭代是否滿足了停止條件(預設的迭代次數),如果滿足就停止。否則,令k=k+1,轉到步驟(2),繼續運行。
經若干次迭代後,使得yk(t)→yd(t);
該迭代學習控制開閉環p型學習律若滿足||i-γ1(t)d(t)||·||[i+γ2(t)d(t)]-1||<1,則控制律收斂;由此可計算出γ1(t)、γ2(t)的值;
然而,迭代學習控制動態性能較差,對此採樣兩電感電流作為內環控制,由於電流比電壓有更快的響應速度,系統的許多變化都會第一時間在電流上有所表現,所以內環電流控制能起到增強系統穩定性和提高動態響應性能的能力。
以下為本發明的具體實施過程。
本發明方法的主電路拓撲如圖1所示。
本發明主要研究雙buck全橋逆變器,用電壓迭代學習控制+電流無差拍控制的控制策略來解決周期性擾動問題。具體實例如下:
仿真驗證
為了驗證本發明方法的可行性,在psim下進行仿真實驗。仿真結果驗證了所設計控制策略的效果。
仿真參數選取如下:
表1:系統整體相關參數
圖3為傳統雙環pid控制輸出電壓仿真波形圖,由圖可以看出系統能很好跟蹤參考波形。
圖4為迭代學習控制下輸出電壓仿真波形圖,由圖可以看出thd值只有2.03%。
圖5為迭代學習控制下參考和實際輸出電壓仿真波形圖,由圖可以看出在0.17s處系統完全跟蹤。
圖6為加周期性擾動後傳統雙環pid控制輸出電壓仿真波形圖,由圖當加入擾動時,傳統雙環控制策略下的輸出波形發生波動,thd達6.03%;圖7是迭代學習控制下加周期性擾動後參考與實際輸出電壓波形圖,由圖可以看出迭代學習控制策略下輸出電壓波形能迅速消除擾動影響且短時間內達到完全跟蹤,thd為1.32%。
由上述說明了本發明具有較好的負載適應能力和優越的跟蹤性能。
以上是本發明的較佳實施例,凡依本發明技術方案所作的改變,所產生的功能作用未超出本發明技術方案的範圍時,均屬於本發明的保護範圍。
