一種求解並行機作業車間調度的混合啟發式轉移瓶頸算法的製作方法

2024-02-11 02:04:15

本發明涉及計算機執行製造系統領域，具體來說就是通過算法解決作業車間

調度的組合優化問題。

背景技術：

調度指給任務分配有限的資源，以優化目標函數。在調度領域，作業車間調度問題(Job-Shop Scheduling Problem，JSP)被認為是最難的組合優化問題之一，是複雜的設備製造系統和柔性製造系統領域中研究的重要課題。解決這個問題具有重要意義，因為即使改善一點效率也可能帶來顯著經濟回報。

JSP是NP-hard問題。JSP的高度複雜性使得它難以在大多數情況下用合理時間找到最優解。許多啟發式算法被提出用於解決JSP，包括基於優先權調度規則的算法、局部搜索算法、移動瓶頸算法、模擬退火算法和禁忌搜索算法。此外，仿生技術如粒子群算法、人工蜂群算法，也被廣泛用於尋找調度問題的最少總完工時間。

各種針對JSP的重要方法都有其局限性：(1)轉移瓶頸算法：可能導致不可行解(2)禁忌搜索算法：不同問題規模，單一搜索策略不會產生最優解；(3)針對多目標的柔性作業車間調度問題的粒子群算法：對於大數據集，不產生最優解；(4)並行化技術解決作業車間調度問題：需實現令牌方法，如果令牌丟失或令牌生成失敗，則算法將失效；(5)多GPU集群執行分布式禁忌搜索算法：僅適用於柔性作業車間調度問題，不適用於並行機作業車間調度問題。

技術實現要素：

針對現有技術中存在的上述不足之處，本發明結合轉移瓶頸算法(Shifting Bottleneck Procedure，SBP)和啟發式禁忌搜索方法，提出了一種混合轉移瓶頸算法(Hybrid Shifting Bottleneck Procedure，HSBP)，並進一步利用GPU實現了並行禁忌搜索算法。減少了找到最優解的計算時間。

本發明的目的則是克服現有技術中存在的：轉移瓶頸算法可能導致不可行解；搜索空間將產生近似解，而不是精確解；隨著問題規模的擴大，搜索時間顯著提高的問題。

本發明為實現上述目的所採用的技術方案是：一種求解並行機作業車間調度的混合啟發式轉移瓶頸算法，該算法包括以下步驟：

步驟1：設置已排序的機器集初始化JSP，建立相應的PDG，PDG包含所有的合取弧，不包含析取弧

步驟2：對所有未排序的機器使用拓撲排序算法,分解並行機JSP的PDG為一組SMS或者PMS子問題。

步驟3：求解每個SMS和PMS子問題，使用改進的Carlier算法求解SMS問題，使用Jackson算法求解PMS子問題。

步驟4：確定瓶頸機k,根據步驟3的結果確定瓶頸機k上的工件工序。更新M0＝M0∪{k},更新PDG。

步驟5：對當前的PDG重新排序和優化。重新調度步驟四的瓶頸機k，使用基於GPU的禁忌搜索算法對PDG進行優化。

步驟6：重複步驟2至步驟5直到所有機器都被調度為止。

本發明的有益效果是：1.轉移瓶頸算法可能導致不可行解，而混合轉移瓶頸算法克服了這一缺點；2.避免了搜索結果不穩定，能找到最優解；3.減少了找到最優解的計算時間。且隨著JSP問題規模的擴大，加速效果更明顯。

附圖說明

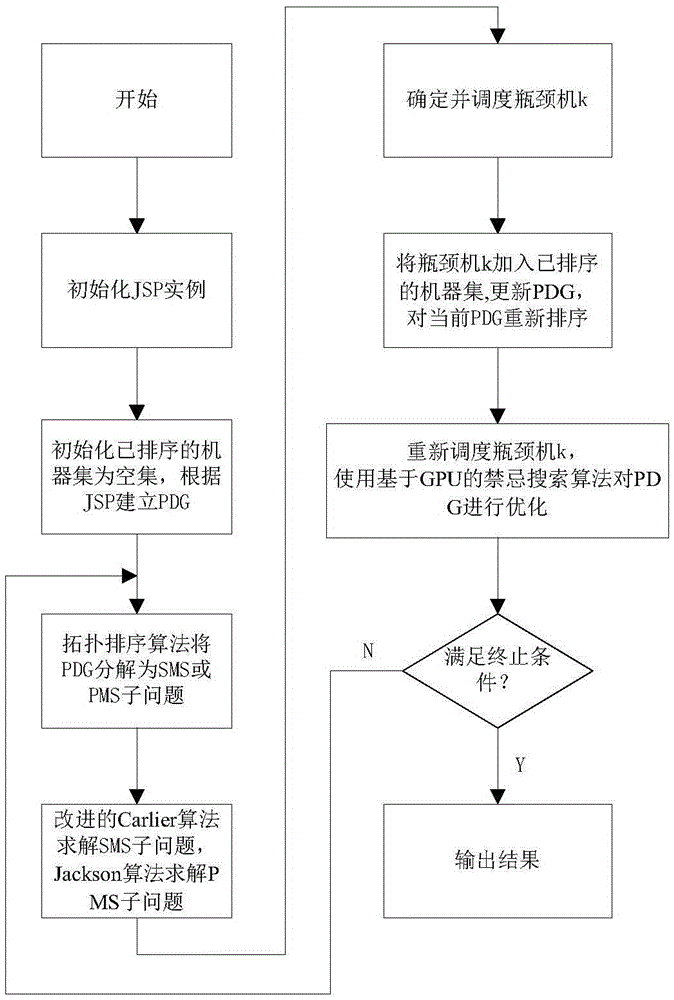
圖1：表示該混合算法詳細流程圖。

圖2：表示一個4*3的JSP實例的合取弧圖。

圖3：表示一個4*3JSP實例的DG模型圖。

圖4：表示該混合算法中禁忌搜索算法的框架圖。

具體實施方式

為了使本發明的目的、技術方案及優點更加清楚明白，以下，結合附圖對本發明進行詳細說明。

一、JSP調度問題

JSP是一個機器調度和優化問題。JSP的特徵：包括N個工件M臺機器的有限集；每個工件包含一條工序鏈；每臺機器同一時刻最多處理一個工序；每個工序需要在給定機器上不間斷處理一段時間；目標是找到加工總時間最短的調度方案。

析取圖(Disjunctive Graph，DG)模型可用於表示JSP，圖G＝{V，C∪D}表示的一個示例如圖2所示。DG模型的描述：DG模型中有n個工件，m臺同樣類型的機器；從1到N標記節點，N表示DG中總工序數量；弧(i，j)連結節點i和節點j，表示工序i必須在工序j之前加工；每條弧對應著工序i的加工時間。在析取圖中，V表示工件的工序，C指工序之間加工的先後約束的合取弧集，D指每對工序必須在相同機器上加工的析取弧集。

JSP實例(n＝3，m＝4)的DG模型圖，結合圖3。其中，析取弧用虛線表示，合取弧用實線表示。虛線表示相同機器上工件可能的順序，而實線表示每個工件的工序順序。析取圖中從虛擬開始節點到虛擬終止節點的最長路徑長度等於調度的總完工時間。

二、並行機作業車間調度的框架

轉移瓶頸算法(Shifting Bottleneck Procedure，SBP)是解決JSP的最佳方法之一，但原始的SBP不能處理並行機。通過嵌入元啟發式思想，SBP將更高效。首先，建立一個局部析取圖(partial disjunctive graph，PDG)，PDG中定向析取弧連結排好序的機器，無向析取弧連結未排好序的機器。針對給定的PDG，並行機作業車間調度可以分解為一組不同釋放時間的單機調度SMS(single-machine scheduling)或者並行機調度PMS(parallel-machine scheduling)子問題。分解後生成的SMS和PMS子問題的數量等於PDG中未排序的單臺機器和並行機的數量。

三、本發明對原有SBP進行了四項改進來解決並行機作業車間調度問題：

(1)拓撲排序算法：分成SMS和PMS子問題。

(2)Carlier算法：求解SMS子問題

(3)Jackson算法：求解PMS子問題

(4)啟發式算法：並行機禁忌搜索

四、所述的拓撲排序算法是用來分解並行機作業車間調度為一組SMS或者PMS子問題，其步驟如下：拓撲排序算法步驟：

(1)對PDG進行拓撲排序，並得到拓撲序列

(2)確定序列中的每一工序的釋放和交貨時間

(3)對涉及的機器分組工序

五、所述的Carlier算法是解決步驟2中拓撲排序算法得到的SMS子問題，它在可選的工件上充分利用Schrage算法，首先加工具有最高交貨時間的工件。

本發明對Schrage算法的改進：考慮滿足一定條件的長尾工件。設ri為釋放時間，qi為交貨時間，pi為處理時間：

在Schrage算法中，(1)如果ri＜rj且qi＞qj，工件i先於工件j加工在邏輯上是正確的。(2)如果ri＜rj且qi＜qj，則工件i和工件j誰先加工存在歧義，事實證明在這種情況下，工件j先於工件i加工的必要條件是qj-qi＞m且pi＞m，其中m＝rj-t，t＝max{c，ri}，c為工件i加工之前的工件的完工時間。

本發明改進的Carlier算法其步驟為：

(1)對當前SMS實例應用Schrage算法，保存Schrage調度得到的結果；

(2)如果存在幹擾工件w滿足qw＜qc，則幹擾工件w在關鍵集之後加工，然後返回本步驟1；

(3)根據保存的結果，選擇最小總完工時間的最佳Schrage調度。

六、所述Jackson算法是解決並行機調度PMS子問題。一個PMS問題定義為一組n個獨立的單工序工件在機器的l個並行單元上調度，工件的每一工序可以在任意可選的單元調度。目標是得到每一工件的完工交貨時間最小的調度。

本發明的Jackson算法的步驟為：

(1)在所有未被調度的工件上選擇具有最高交貨時間的工件A；

(2)調度工件A到具有最小可用時間的第l個並行機上。

七、所述的基於GPU的禁忌搜索算法，結合圖4，是一種並行元啟發式算法，本發明為了用更少的時間得到最優解，用並行編程實現了禁忌搜索算法，多個CPU通過互相發送和接收解的策略來協作。這種方法增加了找到全局最優值的概率，使多個禁忌搜索算法在多個CPU上同時執行，利用GPU的多核架構，這些搜索算法的計算速度將得到提高。

本發明基於GPU的禁忌搜索算法的步驟如下：一個agent首先運行禁忌搜索算法，然後通過發送和接收解與其他agent進行交互。每個agent都擁有一個精英集合，集合中的每個元素是一個高質量的解，是當前agent找到的最好的一些解。一個精英集合使agent能夠跟蹤高質量的解，這些解要麼是自己發現的，要麼是在通信過程中從其他agent得到的。

上述結合附圖對本發明的實施例作了詳細描述，應該理解上述只是示例性的，因此，本發明的保護範圍應當由所附的權利要求書的內容確定。