基於靜應變極值預測的鐵路鋼橋靜載性能評估方法與流程

2024-02-28 13:45:15 3

本發明涉及鐵路鋼橋靜載性能評估領域，具體涉及一種基於靜應變極值預測的鐵路鋼橋靜載性能評估方法。

背景技術：

鐵路鋼橋的靜載性能直接關係到鐵路列車的運營安全，若在環境荷載作用下鐵路鋼橋的關鍵構件超過最大允許值而未能及時發現和整治，會十分危險，甚至發生梁斷車毀的災難性事件，因此開展鐵路鋼橋的靜載性能評估工作具有重要意義。

目前，已有研究工作者針對鐵路鋼橋關鍵構件的應變狀態進行重點監測，並選取監測數據的應變極值與理論設計最大值比較，從而判斷現階段鐵路鋼橋的靜載性能。然而這一種方法存在一個缺點，即有限監測數據的應變極值不能代表鐵路鋼橋在整個運營期內的應變極值，因此無法實現對鐵路橋梁在整個服役期內的靜載性能評估。另有研究工作者嘗試利用監測數據應變極值的概率統計特性對鐵路橋梁在整個服役期內的靜載性能進行評估，但此方法仍存在兩個問題有待解決：(1)所採用的應變極值是一天內應變曲線的最大值和最小值，但一天內應變曲線的最大值和最小值並不一定是極值，即有可能是應變曲線的端點值，因此提取的應變極值數據不夠準確；(2)應變極值的概率統計特性採用概率密度函數來描述，然而概率密度函數與應變極值概率密度柱狀圖的柱條寬度有關，導致概率密度函數失去唯一性。

技術實現要素：

針對現有技術中存在的缺陷，本發明的目的在於提供一種名稱。

為達到以上目的，本發明採取的技術方案是：一種基於靜應變極值預測的鐵路鋼橋靜載性能評估方法，該方法包括如下步驟，

步驟a.在採樣時間L天內採集鐵路橋梁關鍵構件受力最不利位置的應變數據；

步驟b.利用小波包分析方法提取所述應變數據中的靜應變成分；

步驟c.以天為單位對所述靜應變成分進行劃分，對每天內的所有靜應變值按照採集先後順序做一階差分處理，得到靜應變值在每天的差分序列，將每一天內的所述差分序列任意分割為多份，並對每一份所述差分序列各自求和，再對每一份所述差分序列的求和結果取絕對值並相加求得總和，在分割份數相同的情況下比較在不同分割點下求得的所述總和的大小，確定所述總和最大時的分割點，比較所述差分序列在所述總和最大時的分割點下的大小，從而確定每天內所述靜應變成分中日變化極大值和日變化極小值，進而確定並比較所述採樣時間L天內所述靜應變成分中日變化極大值DMAX和日變化極小值DMIN；

步驟d.利用廣義極值分布函數G(DMAX)和F(DMIN)分別擬合所述採樣時間L天內所述靜應變成分中日變化極大值DMAX和日變化極小值DMIN的累加分布特性：

步驟e.對所述鐵路橋梁關鍵構件受力最不利位置進行靜載性能評估：其中，

式中，P為超越概率，利用牛頓迭代法並結合所述廣義極值分布函數G(DMAX)和F(DMIN)，求解方程(4)和方程(5)，確定超越概率為P時的靜應變標準值和

用表示和中的絕對值最大者，將與設計允許值比較判斷所述鐵路橋梁的靜載性能，若則所述鐵路橋梁關鍵構件受力最不利位置的靜載性能處於安全狀態；反之，則所述鐵路橋梁關鍵構件受力最不利位置的靜載性能處於非安全狀態。

在上述技術方案的基礎上，所述步驟a中採用光纖光柵應變傳感器採集所述應變數據，並以光纖光柵溫度傳感器作為溫度補償。

在上述技術方案的基礎上，所述步驟a中採樣時間L大於200天，且採樣頻率大於1/600Hz小於1Hz。

在上述技術方案的基礎上，所述小波包分析方法具體包括將採集到的所有所述應變數據按照採集先後順序構成應變序列，後將所述應變序列進行第c個尺度上的小波包分解，得到2c個小波包係數，提取出第一個小波包係數並對其重構，得到所述應變序列中的靜應變成分，其中c為測量點個數係數。

在上述技術方案的基礎上，所述測量點個數係數c等於5。

在上述技術方案的基礎上，所述步驟c中的每一天的差分序列被任意分割為三份。

在上述技術方案的基礎上，所述採樣時間L天內所述靜應變成分中日變化極大值DMAX的累加分布特性的擬合包括，計算所述日變化極大值DMAX的累加概率值，並利用所述廣義極值分布函數G(DMAX)對其擬合，其中：

式中，b、d和r分別表示G(DMAX)的尺度參數、位置參數和形狀參數，將計算求得的日變化極大值DMAX和日變化極大值DMAX的累加概率值分別代入式(2)中，利用最小二乘法確定b、d和r的最佳取值；

所述採樣時間L天內所述靜應變成分中日變化極小值DMIN的累加分布特性的擬合包括，計算所述日變化極小值DMIN的累加概率值，並利用所述廣義極值分布函數F(DMIN)對其擬合，其中

式中，g、h和λ分別表示F(DMIN)的尺度參數、位置參數和形狀參數，將計算求得的日變化極小值DMIN和日變化極小值DMIN的累加概率值分別代入式(3)中，利用最小二乘法確定g、h和λ的最佳取值；

在上述技術方案的基礎上，所述超越概率P的取值為0.01。

與現有技術相比，本發明的優點在於：

(1)本發明中的基於靜應變極值預測的鐵路鋼橋靜載性能評估方法，其利用一階差分確定應變極值，從而有效避免應變最大值或最小值不是應變極值的情況，使得提取的應變極值數據更加準確。

(2)本發明中的基於靜應變極值預測的鐵路鋼橋靜載性能評估方法，其利用累加概率值克服了傳統方法中概率統計特性沒有唯一性的缺點，保證了應變極值概率統計特性的唯一性，而且本方法更能準確有效地對鐵路橋梁在整個服役期內的靜載性能評估，可得到廣泛推廣和應用。

附圖說明

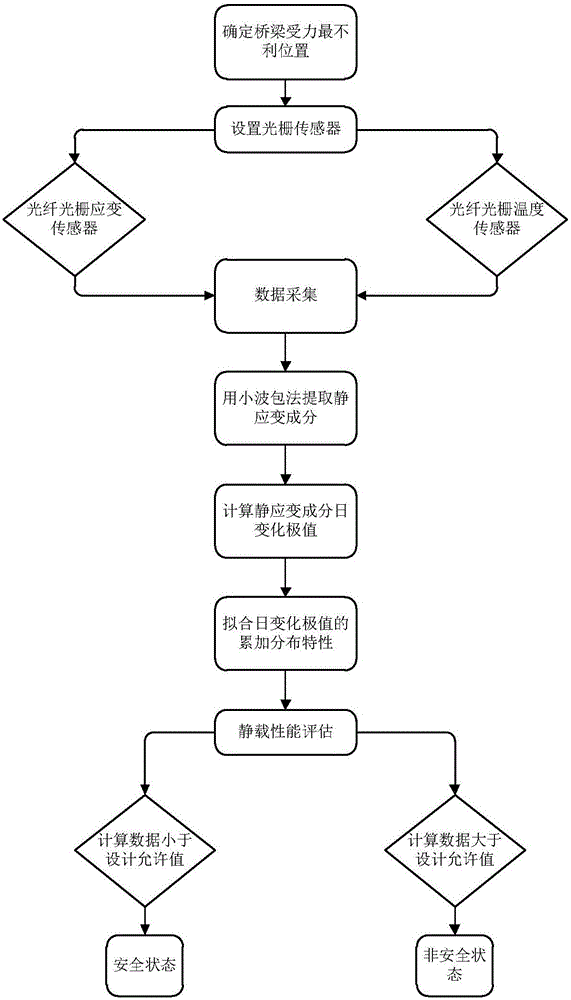
圖1本發明中評估方法的流程圖；

圖2為本發明實施例中大勝關長江大橋的立面圖；

圖3為本發明實施例中光纖光柵應變傳感器的布置位置；

圖4為本發明實施例中所有應變值按照採集先後順序構成的應變序列；

圖5為本發明實施例中應變序列中的靜應變成分；

圖6為本發明實施例中日變化極大值的變化曲線；

圖7為本發明實施例中日變化極小值的變化曲線；

圖8為本發明實施例中日變化極大值廣義極值分布的擬合結果；

圖9為本發明實施例中日變化極小值廣義極值分布的擬合結果。

圖中：1-上弦杆，2-光纖光柵溫度傳感器。

具體實施方式

以下結合附圖及實施例對本發明作進一步詳細說明。

本發明提供一種基於靜應變極值預測的鐵路鋼橋靜載性能評估方法，參見圖1所示的流程圖，該方法包括以下步驟：

步驟a.對鐵路橋梁關鍵構件的最不利位置進行應變數據採集：

本發明將光纖光柵應變傳感器配接到數據採集系統中，並以光纖光柵溫度傳感器作為溫度補償，對鐵路橋梁關鍵構件的最不利位置進行數據採集，受力最不利位置指的是橋梁受力最大、最集中處或橋梁結構最為容易破壞處。採樣頻率表示為fHz，採樣時間長度用L表示，採集到的第i個應變值採用S(i)表示，i＝1,...,M，M為應變值總個數。其中，採樣頻率大於1/600Hz小於1Hz，採樣時間L大於200天。

步驟b.利用小波包分析方法提取應變數據中的靜應變成分：

由於應變數據明顯受到列車荷載的幹擾，因此利用小波包分析方法提取出應變數據中不受列車荷載幹擾的靜應變成分。其中小波包分析方法是一種信號處理與分析的常用方法，可以根據信號特性和分析要求自適應地選擇相應頻帶與信號頻譜相匹配，是一種精細的信號分解方法，其具體操作為：將採集到的所有應變值S(i)按照採集先後順序構成應變序列，後將應變序列進行第c個尺度上的小波包分解，得到2c個小波包係數，提取出第一個小波包係數並對其重構，得到應變序列中的靜應變成分，其中c為測量點個數係數。

步驟c.利用一階差分獲取靜應變成分中的日變化極值：

1.以天為單位對靜應變成分進行劃分，靜應變成分在第m天內的第j個靜應變值採用Sm(j)表示，其中m＝1,2,...,L，j＝1,2,...,Nm，Nm為靜應變值在第m天內的總個數。

2.對每天內的所有靜應變值按照採集先後順序做一階差分處理，一階差分處理指的是靜應變值中連續相鄰兩項之差，從而得到靜應變值在每天內的差分序列。其中差分序列在第m天內的第k個值採用Dm(k)表示，k＝1,2,...,Nm-1。

3.每一天的差分序列可以根據需要被任意分割為多份，本發明中的差分序列被分割為三份，為了歸納說明，本發明將第m天內的差分序列{Dm(1),Dm(2),...,Dm(Nm-1)}分割為三份，其中第一份差分序列為{Dm(1),Dm(2),...,Dm(p1,m)}，第二份差分序列為{Dm(p1,m+1),Dm(p1,m+2),...,Dm(p1,m+p2,m)}，第三份差分序列為{Dm(p2,m+1),Dm(p2,m+2),...,Dm(Nm-1)}，其中p1,m、p2,m分別為第m天內差分序列的兩個分割點，且滿足1＜p1,m＜p2,m＜Nm-1。

4.對三份差分序列中的所有值求和，用Zm,l(p1,m,p2,m)表示第m天內取值為p1,m,p2,m時第l份差分序列之和，其中l＝1,2,3，然後按照下式求得Zm,1(p1,m,p2,m)、Zm,2(p1,m,p2,m)和Zm,3(p1,m,p2,m)三者之和：

Qm(p1,m,p2,m)＝|Zm,1(p1,m,p2,m)|+|Zm,2(p1,m,p2,m)|+|Zm,3(p1,m,p2,m)| (1)

式中，Qm(p1,m,p2,m)的計算結果與p1,m，p2,m取值有關，對p1,m，p2,m選取在約束條件1＜p1,m＜p2,m＜Nm-1下所有可能的取值，代入式(1)中計算出相應的Qm(p1,m,p2,m)值，所有Qm(p1,m,p2,m)值中必然存在一個最大值，假設此最大值是由p1,m＝a1,m、p2,m＝a2,m得到的，則第m天內靜應變成分中的日變化極大值為Dm(a1,m)和Dm(a2,m)兩者中的較大值，日變化極小值為Dm(a1,m)和Dm(a2,m)兩者中的較小值，在確定出第m天內靜應變成分中的日變化極大值和極小值後，通過比較每天的日變化極大值和極小值，從而確定在所有天數L內的日變化極大值和極小值，其中所有天數L內的日變化極大值採用DMAX表示，所有天數L的日變化極小值採用DMIN表示。

本發明利用一階差分確定應變極值，從而有效避免應變最大值或最小值不是應變極值的情況，使得提取的應變極值數據更加準確。

步驟d.利用廣義極值分布函數擬合日變化極值的累加分布特性：

1.計算日變化極大值DMAX的累加概率值，在概率與數理統計理論中，累加概率值定義為統計變量不超過某一數值的發生概率，並利用廣義極值分布函數對其擬合：

式中，G(DMAX)表示的廣義極值分布函數，b、d和r分別表示G(DMAX)的尺度參數、位置參數和形狀參數，將計算求得的日變化極大值和日變化極大值DMAX的累加概率值分別代入式(2)中並利用最小二乘法確定b、d和r的最佳取值；

2.計算日變化極小值的累加概率值，並利用廣義極值分布函數對其擬合：

式中，F(DMIN)表示的廣義極值分布函數，g、h和λ分別表示F(DMIN)的尺度參數、位置參數和形狀參數，將計算求得的日變化極小值和日變化極小值DMIN的累加概率值分別代入式(3)中並利用最小二乘法確定g、h和λ的最佳取值。

步驟e.對所述鐵路橋梁關鍵構件受力最不利位置進行靜載性能評估：

利用牛頓迭代法求解方程(4)和方程(5)，確定超越概率為P時的靜應變標準值和超越概率指在一定時期內，可能遭遇大於或等於給定參數值的概率。

用表示和中的絕對值最大者，將與設計允許值比較判斷所述鐵路橋梁的靜載性能，若則所述鐵路橋梁關鍵構件受力最不利位置的靜載性能處於安全狀態；反之，則所述鐵路橋梁關鍵構件受力最不利位置的靜載性能處於非安全狀態。

牛頓迭代法是一種求解方程根的重要方法，其最大優點是在方程或的單根附近平方收斂；按照鐵路橋梁的100年設計服役期考慮，超越概率P的取值為0.01。

下面以大勝關長江大橋的弦杆軸向應變為例，說明本發明的具體實施過程。

參見圖2所示大勝關長江大橋的立面圖，以及圖3所示光纖光柵應變傳感器布置位置示意圖，將光纖光柵應變傳感器2安裝在大勝關長江大橋跨中邊桁上弦杆1的軸向位置，並配接到數據採集系統中，以光纖光柵的溫度傳感器作為溫度補償，對上弦杆1軸向應變進行數據採集。採樣頻率f為1Hz，採樣時間長度L為232天，採集到的第i個應變值採用S(i)表示，i＝1,...,33408。

參見圖4所示，其為大勝關長江大橋所有應變值S(i)按照採集先後順序構成的應變序列。

參見圖5所示，將應變序列進行第5個尺度上的小波包分解，得到32個小波包係數，提取出第一個小波包係數並對其重構，得到應變序列中的靜應變成分。

以天為單位對靜應變成分進行劃分，靜應變成分在第m天內的第j個靜應變值採用Sm(j)表示，其中m＝1,2,...,232，j＝1,2,...,144。對每天內的所有靜應變值按照採集先後順序做一階差分處理，得到靜應變值在每天內的差分序列，差分序列在第m天內的第k個值採用Dm(k)表示，k＝1,2,...,143。

根據上述步驟c中的第3和第4步確定232天內的日變化極大值DMAX和日變化極小值DMIN，分別參見圖6和圖7所示。根據步驟d中相關計算步驟，利用最小二乘法確定b、d和r以及g、h和λ的最佳參數取值，其中b＝41.3228、d＝33.0127、r＝-0.4071；g＝54.4519、h＝-24.6663、λ＝-0.612298，代入各個數值計算得到日變化極大值廣義極值分布的擬合結果和日變化極小值廣義極值分布的擬合結果，分別參見圖8和圖9所示。

利用牛頓迭代法對上述步驟e中的方程(4)和方程(5)求解，確定具有超越概率為P的靜應變標準值和其中：超越概率P為0.01。

計算結果為：然後選取和中的最大絕對值，即將與設計允許值比較判斷鐵路橋梁的靜載性能：已知大勝關鐵路橋梁鋼材選用Q420，則可知則關鍵構件受力最不利位置的靜載性能處於安全狀態。

本發明不局限於上述實施方式，對於本技術領域的普通技術人員來說，在不脫離本發明原理的前提下，還可以做出若干改進和潤飾，這些改進和潤飾也視為本發明的保護範圍之內。本說明書中未作詳細描述的內容屬於本領域專業技術人員公知的現有技術。