標量的足長規則NAF序列的生成方法與流程
2023-05-15 22:04:47 3
本發明涉及信息安全領域,特別是涉及一種標量的規則NAF(非相鄰表示型)序列在多標量組合點乘運用時的生成方法。
背景技術:
橢圓曲線密碼系統(ECC)具有安全性高、計算量小、處理速度快、存儲空間小、帶寬要求低等特點。與RSA公鑰體制相比,ECC非常適合於資源有限的嵌入式移動環境,如智慧卡(smartcard)上的密碼晶片。傳統上,對密碼晶片的攻擊主要是對實現的算法從數學角度進行分析,如差分分析和線性分析。但自從旁路攻擊(Side Channel Attacks)被提出以後,人們越來越多的開始關注晶片的實現,以及針對晶片所面臨的攻擊所採取的抗攻擊措施。旁路攻擊(Side Channel Attacks)是一種利用密碼晶片在運算過程中無意洩露出的信息,比如指令執行時間、功耗、電磁輻射等信息,對晶片進行攻擊的一種方法。與傳統的攻擊方法相比,其密鑰的搜索空間大大小於差分密鑰分析和線性密鑰分析。按攻擊特點的不同,旁路攻擊可以分為時間攻擊、功耗分析攻擊和電磁輻射攻擊等幾種類型。功耗分析技術分為簡單功耗分析(SPA)和差分功耗分析(DPA),SPA是指根據功耗曲線上所呈現的特殊特徵來推測密鑰信息,DPA利用的是操作數的變化所引起的微小的功耗變化,需要通過對大量功耗曲線進行統計分析,最終得出密鑰信息。
標量乘是ECC最重要最耗時的運算,對ECC的功耗攻擊也主要集中在對標量乘運算的攻擊,快速而安全的實現標量乘對於ECC來講至關重要。設E(Fq)是定義在有限域Fq上的橢圓曲線,P(x,y)是E(Fq)上的點。若Fq是二元域,則-P=(x,x+y);若Fq的特徵大於3,則-P=(x,-y)。因此橢圓曲線點的減法和點的加法一樣有效。這使得人們可以使用標量k的帶符號數學表示,一種特別有用的帶符號數學表示是非相鄰表示型(NAF),對於一個標量k有唯一的NAF表示。Width-w NAF算法是帶有預計算表的NAF算法的一種擴展形式,它具有連續的w位數中非零的個數最多為1的特點,因此常用於標量乘的快速實現。每一個標量k都有唯一的Width-w NAF表示,而非0位的位置也與標量k本身的數值有直接的關係,這不利於抗簡單功耗分析(SPA)攻擊。
一種有效抵禦SPA攻擊的方法是為標量k產生規則的Width-w NAF表示,在這種規則Width-w NAF序列中每w位數中一定會也只會在特定的位置產生非0位,因而非0位的位置與標量k本身的數值沒有直接的關係,在標量乘的功耗曲線上也就沒有明顯的特徵可供SPA所利用。其算法如下:輸入:正整數k,窗口寬度w;
輸出:k的規則序列窗口NAF表示kw;
1.r=0,i=0,r0=w;
2.若k為偶數,則k=k+1;
3.當k大於1時,重複執行;
3.1u[i]=(k mod 2w+1)-2w;
3.3kw[r+ri-1]=0,…,kw[r+1]=0,kw[r]=u[i];
3.4r=r+ri,i=i+1,ri=w;
4.kw[n]=0,…,kw[r+1]=0,kw[r]=1;
5.返回kw[n],kw[n-1],…,kw[0]。
由於該方法只能處理奇數的標量,對於偶數標量可以做加1處理,最後在標量乘結束後再進行調整就可以了:(k+1)P-P。這個方法首先是要根據所選擇的窗口大小w為標量k計算規則的NAF序列並存儲,根據窗口大小計算需要預計算的點並存儲,然後再進行標量乘計算,最後根據標量k的奇偶性決定是否需要對結果進行調整。
標量乘也經常採用固定基窗口方法、多點乘窗口方法等方法來加速運算,在這些點乘計算方法中存在多段標量進行組合計算,這些方法需要大量的預計算和存儲空間,計算過程的邏輯複雜性也會比單標量點乘計算的複雜性要大。如果在多標量組合時標量不等長,會進一步增加預計算和存儲空間,邏輯複雜性也會進一步增加。
技術實現要素:
本發明要解決的技術問題是提供一種標量的足長規則NAF序列的生成方法,能在採用規則NAF序列的多標量組合點乘中,統一各標量的長度:減少預計算的計算量和存儲空間,降低邏輯實現的複雜度。
為解決上述技術問題,本發明的標量的足長規則NAF序列的生成方法,包括如下步驟:
步驟1、根據需求選擇規則NAF序列的窗口大小w,w為大於1的正整數,列出相應窗口大小下規則NAF序列的格式,以及序列中的各種可能的帶符號數值X;
步驟2、計算窗口大小為w的標量的規則NAF序列,以帶符號的數值表示之;
步驟3、對於不足長的序列,將計算所得最高位窗口中的1移到足長最高位窗口中,並以相應窗口大小下規則NAF序列中最大的負值填充到足長最高位窗口與計算次高位窗口之間的各窗口中;
步驟4、以步驟3中計算所得足長的規則NAF序列參與後續的運算。
採用本發明的方法產生的標量k的規則NAF序列能夠保證足長,在多段標量進行組合計算的點乘運算中,不需要因為標量不足長而增加預計算的存儲空間和運算過程的複雜度。
附圖說明
下面結合附圖與具體實施方式對本發明作進一步詳細的說明:
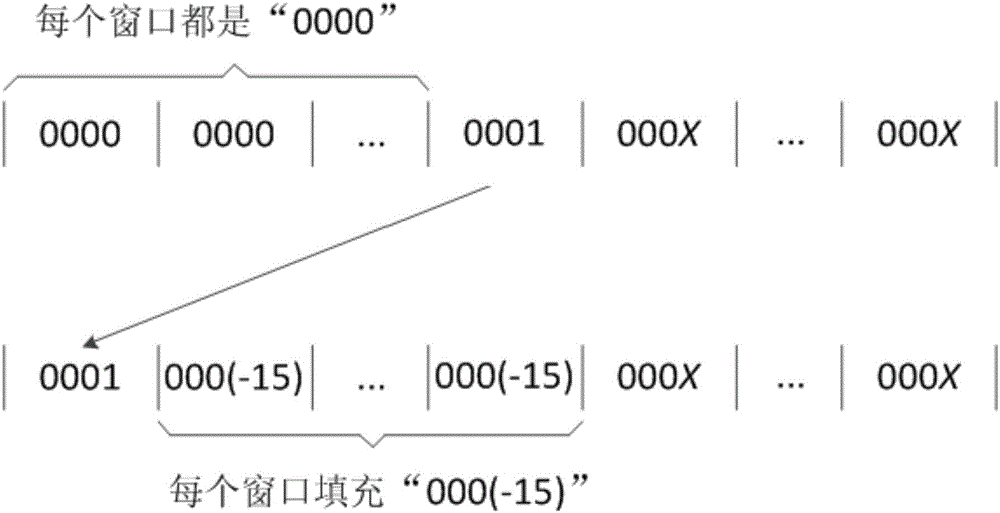
圖1是規則序列從不足長到足長的變化示意圖。
具體實施方式
結合圖1所示,下面以窗口w=4為例來介紹所述標量的足長規則NAF序列的生成方法。
(1)選擇窗口w=4的規則NAF序列,默認數值按左高右低排列,其格式為:0001000X000X…000X。
(2)窗口w=4的規則NAF序列中非0的X∈{-15,-13,-11,-9,-7,-5,-3,-1,1,3,5,7,9,11,13,15}。
(3)根據標量k的最低位記錄其奇偶性並調整最低位得到奇數的k』,若k[0]=1,則k』=k,否則,k』=k+1。
(4)為標量生成窗口w=4的規則NAF序列。
(5)如果不足長,則將計算所得最高位窗口中的1移到足長最高位窗口中,並將-15填充到足長最高位窗口與計算次高位窗口之間的各窗口中,由此產生的足長規則序列與原始規則序列在數學上的數值完全一致,不影響點乘計算的正確性。
(5)其餘點乘步驟不變。
圖1中上端為原始規則序列,下端為修改後足長的規則序列。
以上通過具體實施方式對本發明進行了詳細的說明,但這些並非構成對本發明的限制。在不脫離本發明原理的情況下,本領域的技術人員還可做出許多變形和改進,這些也應視為本發明的保護範圍。
