一種高錳鋼拋丸機葉片噴丸強化工藝參數的確定方法與流程
2023-05-15 04:49:56 2
本發明涉及噴丸加工技術領域,尤其是涉及一種高錳鋼拋丸機葉片噴丸強化工藝參數的確定方法。
背景技術:
目前國內外拋丸機的應用日益廣泛,不再局限於傳統的零件表面處理,更廣泛應用於維護和修復高速公路、鋼橋和機場路面等。拋丸器作為拋丸機的關鍵部件,其質量與使用壽命直接取決於葉片,而葉片工作時因要承受磨料對其表面的磨損,從而成為拋丸機中最易損壞的部位。據不完全統計,每年國內僅因葉片磨損而消耗的材料價值上千萬。而噴丸工藝使工件表面發生塑性變形,形成一層具有加工硬化效果的表面強化層。研究認為,表面強化層的存在不僅提高了工件表面的硬度和耐磨性,更重要的是在工件的表層形成了殘餘壓應力層,殘餘壓應力層能夠阻礙疲勞微裂紋的生成和擴展,從而極大地提高零件的表面疲勞抗力。
高錳鋼作為一種傳統的耐磨材料,在重載、大衝擊磨損條件下,韌性高、耐磨性好,廣泛應用於冶金、礦山、建材、鐵路、電子、煤炭等機械裝備中,如破碎機錘頭、齒板、軋臼壁、挖掘機鬥齒、球磨機襯板和鐵路轍叉等。高錳鋼屬於奧氏體組織的鋼種,在高衝擊載荷下使用,耐磨性好,安全可靠,它不僅可用較低價的原材料製成且易冶煉,並有較好的鑄造性能。因此,高錳鋼一直是承受高衝擊負荷或者金屬與金屬直接接觸下要求具有高抗磨性的理想材料。
目前,噴丸工程應用主要依靠經驗和試噴,存在工藝參數選擇不合理、強化效果不理想的問題,並且採用目前的殘餘應力測試手段和方法,特別是無損檢測方法,難以完全掌握三維殘餘應力場,且經驗和試噴需耗費大量的時間和人力,這些因素都極大制約了噴丸技術的發展。
對於噴丸強化這一高度非線性的動態衝擊過程,需要藉助於數值仿真手段進行分析,近年來相關學者開展了數值模擬研究取得了較大進展。但由於噴丸強化作用過程複雜且影響因素眾多,目前仍然缺乏相關的方法來對噴丸過程的參數進行最優設計。
技術實現要素:
本發明的目的在於克服現有技術中存在的缺點,提供一種基於abaqus有限元分析的噴丸強化處理工藝參數確定方法,該模擬方法根據應力等效原理,通過彈丸撞擊法建立噴丸強化殘餘應力有限元模型,模擬得到不同噴丸工藝參數下的殘餘應力分布,從而確定高錳鋼葉片最佳噴丸工藝參數,以提高高錳鋼葉片的使用壽命,且還可以實現根據高錳鋼工件表層最大殘餘應力的需要,定製合適的噴丸強化工藝參數。採用的技術方案是:一種高錳鋼拋丸機葉片噴丸強化工藝參數的確定方法,其特徵是:所述方法按照以下步驟進行:
1)建立有限元模型:
利用彈丸及高錳鋼葉片的材料屬性及尺寸對彈丸及高錳鋼葉片建立abaqus有限元模型,以所建立有限元模型模擬高錳鋼葉片噴丸強化過程,所述彈丸及高錳鋼葉片的材料屬性是以材料參數進行表徵,所述材料參數是指彈丸及高錳鋼葉片的楊氏模量、泊松比、密度、屈服強度以及極限強度;
2)有限元分析:
根據工藝要求採用所述有限元軟體為所述有限元模型中的彈丸及高錳鋼的材料參數、彈丸大小及初速度進行賦值,利用所述有限元軟體獲得高錳鋼葉片表面各節點的平均殘餘應力;
3)逐步回歸分析:
運用正交實驗法設計工藝參數組合,所述工藝參數是指彈丸直徑、彈丸速度和噴丸時間,利用2)所述的有限元分析得出不同工藝參數下拋丸機葉片的最大平均殘餘應力;
4)採用回歸分析得到最大平均殘餘應力關於所述工藝參數的最優回歸方程,利用所述最優回歸方程確定最佳噴丸強化處理工藝參數,方程為:
y=376.272+21.793dt+0.015v2。
本發明的技術特徵還有:步驟1)中所述有限元模型包括直徑為的彈丸,以及從高錳鋼葉片受噴面上截取的以受噴面為頂面的長方體,所述長方體的頂面是與水平面平行且邊長為20mm的正方形;所述長方體的高度為8mm。
本發明的技術特徵還有:拋丸機葉片的網格劃分選用c3d8r單元,噴丸選用c3d4單元。
本發明的有益效果在於:本發明提出的一種基於有限元分析的拋丸機葉片噴丸強化的有限元模擬方法,利用成熟的彈丸撞擊法得到不同噴丸工藝參數下的高錳鋼葉片殘餘應力分布,避免實際生產中常用的噴丸試驗方法所伴隨的成本過高,消耗大量的人力和物力的問題;本發明把多種形式的多項式逐步回歸方法引入噴丸工藝參數最優方程的選取,得到更加精確的回歸方程,增加了獲得噴丸工藝參數的實用性;本發明採用正交實驗安排噴丸工藝參數,運用逐步回歸分析方法進行回歸,最後得到最優回歸方程,可以對最大平均殘餘應力進行定量研究,根據最大平均殘餘應力的需要,可以任意定製工藝參數本發明公開的該模擬方法具有快速化、低成本、簡便易行、計算準確的特點,工程實際應用效果好。
附圖說明
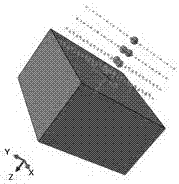
附圖1是本發明中覆蓋率100%的有限元模型;附圖2是本發明中覆蓋率200%的有限元模型;附圖3是本發明中覆蓋率300%的有限元模型;附圖4是本發明中覆蓋率400%的有限元模型;附圖5是模擬結果和實驗結果比較示意圖。
具體實施方式
下面結合附圖,對本發明的具體實施方式進行說明。
基於abaqus有限元分析的拋丸機葉片噴丸強化處理工藝參數確定方法是按如下步驟進行:
噴丸強化殘餘應力有限元模擬
在abaqus動態顯示分析中,通過定義彈丸的初始速度來模擬彈丸與高錳鋼葉片表面撞擊過程中所產生的衝擊載荷,同時採用庫侖摩擦模型來描述彈丸和高錳鋼葉片之間的接觸情況,減少兩接觸面之間的切向運動,使計算得到的結果更加穩定;高錳鋼葉片單元類型為c3d8r,在彈丸撞擊區域採用局部細化網格方式劃分單元。在實際噴丸強化過程中,彈丸材料為鋼絲切丸,硬度較高,並且屈服強度及抗拉強度都很高,碰撞後變形很小。在有限元模擬過程中將彈丸約束成剛性體,並且忽略重力加速度的影響,接觸前假定保持勻速運動;通過噴丸強化殘餘應力有限元模擬得到殘餘應力分布結果。
步驟1:建立有限元模型
利用彈丸及高錳鋼葉片的材料屬性對彈丸及拋丸機葉片建立有限元模型,以所建立有限元模型模擬整個高錳鋼葉片噴丸強化過程,並採用非反射邊界條件、對稱面和固定約束減小邊界對於模擬效果的影響;彈丸及高錳鋼的材料屬性以材料參數表徵,材料參數是指彈丸及高錳鋼的楊氏模量、泊松比、密度、屈服強度以及極限強度,具體參數如表1所示。
表1高錳鋼及彈丸材料工藝參數
建立實體模型:葉片尺寸為20×20×8mm,彈丸直徑根據正交試驗表設定為0.6mm、0.8mm、1.0mm和1.2mm,噴丸覆蓋分別為100%、200%、300%和400%,如圖1,圖2,圖3和圖4所示為噴丸覆蓋分別為100%、200%、300%和400%的有限元模型。覆蓋率為100%的模型為四層彈丸,以及從葉片上截取的以受噴面為頂面的六面體,六面體的頂面是與水平面平行、且邊長為20mm的正方形;六面體的高度為8mm;彈丸排列方法如圖所示交錯排列,覆蓋率100%為9球,覆蓋率200%為18球,覆蓋率300%為27球,覆蓋率400%為36球。
考慮葉片尺寸對模擬效果的影響,在葉片側面施加非反射邊界條件;在底面施加固定約束以減小震蕩。
採用有限元軟體對接觸進行定義,定義接觸類型為「侵蝕」。
採用有限元軟體對邊界進行設置,為減少邊界對模擬效果的影響,設置葉片除受噴面之外的其它面為非反射邊界。
採用有限元軟體對葉片進行固定約束。
採用有限元軟體對彈丸施加初速度;所述初速度方向與高錳鋼葉片受噴面垂直。
完成有限元模型的建立。
步驟2:有限元分析
根據工藝要求採用有限元軟體為所建立有限元模型中的彈丸及拋丸機葉片的材料參數、彈丸大小及初速度進行賦值,利用有限元工具獲得拋丸機葉片表面受噴部位各單元的殘餘應力σ。
步驟3:逐步回歸分析
運用正交實驗法設計工藝參數組合,工藝參數是指彈丸直徑、彈丸速度和覆蓋率,正交實驗法為實驗參數安排常規方法。
採用有限元軟體設計每一組工藝參數,利用步驟2的有限元分析得出不同工藝參數下高錳鋼葉片表面的最大平均殘餘應力。
採用回歸分析得到最大平均殘餘應力關於工藝參數的最優回歸方程;利用最優回歸方程確定噴丸強化處理工藝參數,回歸分析為數據處理常規方法。
選擇二次多項式函數進行逐步回歸分析,求得回歸方程後進行比較,選擇其中可信度和精度高並且簡單的回歸方程作為所求的最優回歸方程。
為了完全因素的分析噴丸工藝參數對拋丸機葉片的影響,下面建立最大平均殘餘應力與工藝參數(彈丸直徑(0.6mm、0.8mm、1.0mm和1.2mm)、彈丸速度(50m/s、70m/s、90m/s和110m/s)和覆蓋率(100%、200%、300%和400%)之間的關係。本文採用正交試驗法安排噴丸工藝參數,取3因素4個水平,選用l16(34)正交試驗表,針對每一組噴丸工藝參數建立三維實體模型,在abaqus平臺上選用顯式動力求解器,進行網格劃分、設置邊界條件,並進行數值模擬,得到相應的最大平均殘餘應力值,如表2。
表2按照正交實驗安排的工藝參數及計算結果
高錳鋼葉片噴丸強化有噴丸速度、噴丸直徑、噴丸時間三個輸入變量,一個輸出變量為最大平均殘餘應力。採用表3中按正交試驗法安排的參數和計算得到的殘餘應力計算數據,首先對回歸模型進行了調整r方檢驗(兩個回歸模型的調整r方值分別為0.682和0.806,選取接近1的0.806的回歸模型作為最終的回歸模型),回歸模型選定以後,並對回歸模型中的回歸方差和回歸係數檢驗(置信區間為95%)。
步驟4:回歸方差和回歸係數檢驗之後得到的最優回歸方程為:
y=376.272+21.793dt+0.015v2
根據最優回歸方程,可以對各自變量與最大平均殘餘應力的關係做定量的分析。從關係式可以分析任意自變量參數對噴丸強化後高錳鋼葉片表層殘餘應力的影響關係。
步驟5:實驗驗證
為了進一步驗證模擬結果的正確性,採用實驗的方法對模擬結果進行驗證。
採用某集團的氣動式噴丸強化設備,彈丸流量為30kg/min,彈丸直徑為0.8mm,噴丸壓力為0.5mpa。噴丸之後採用美國astx2001x射線應力儀測試噴丸後高錳鋼葉片表層的殘餘應力值,並把模擬計算數值與實驗所得數據應力進行比較,如圖5所示為模擬結果與實驗結果比較。由圖5可見,模擬結果與實驗所測結果曲線十分吻合,說明模擬計算模型合理,最優回歸方程正確,因此可以實現根據高錳鋼工件表層最大殘餘應力的需要,利用本回歸方程定製合適的噴丸強化工藝參數。
