面向約束的可重構機械臂非奇異終端滑模力位置控制方法與流程

2023-05-18 07:20:11 2

本發明涉及一種面向約束的可重構機械臂非奇異終端滑模力位置控制方法，屬於機器人控制方法及受約束系統控制方法領域。

背景技術：

可重構機械臂是一類由不同尺寸和功能特點的機器人模塊構成的裝配組合，可以在不同的外部約束下，重構成多種機械臂構形來滿足不同任務的要求。和傳統的機械臂相比，可重構機械臂由於其具有柔性結構、成本低廉等優勢，因此在航天製造、空間探索、醫療救援、商業服務等領域有很大的應用價值。

在實際應用中，面向約束的可重構機械臂系統的力和位置都需要進行精確的控制。然而，在機械臂控制的整個過程中，控制器的抖振現象時有發生，究其原因，有很多因素會引起抖振效應，例如，傳統的滑模控制可以使控制器自身產生抖振效應；系統的不確定性(如摩擦、耦合)會引起控制器抖振；一些柔性因素(如傳動裝置柔性)也可能引起系統抖振；開關轉換動作引起的控制的不連續也是抖振效應產生的原因。遺憾的是，抖振效應不僅影響系統的控制精度，而且會增加能源消耗，破壞系統性能。

滑模控制作為一種行之有效的控制方法被廣泛應用於機械臂控制系統的設計當中。雖然已經有很多人研究了基於線性滑模和終端滑模技術的機械臂控制方法，但是大多數方法旨在解決自由空間下機械臂系統的位置控制問題，而針對面向約束的可重構機械臂系統力位置控制方法的研究十分有限。

技術實現要素：

本發明為了解決傳統終端滑模控制力位置控制方法中存在的跟蹤精度低、收斂速度慢、存在抖振的問題，提出一種面向約束的可重構機械臂非奇異終端滑模力位置控制方法。在建立面向約束的可重構機械臂系統動力學模型的基礎上，提出一種新穎的非奇異終端滑模函數，引入了rbf神經網絡來補償系統未知非線性項、關節之間耦合項和模型不確定項，並發明了非奇異終端滑模力位置控制方法，使得軌跡跟蹤誤差在有限時間內收斂到零，同時控制器本身具有較強的魯棒性，使得控制器抖振效應得到有效抑制，並使控制信號在整個過程中變得光滑，而且保證了軌跡的跟蹤精度，實現高精度、微抖振的可重構機械臂系統力位置控制。

本發明解決技術問題的方案是：

面向約束的可重構機械臂非奇異終端滑模力位置控制方法，其特徵是，該方法包括如下步驟：

第一步，面向約束的可重構機械臂系統動力學模型通過狀態空間表達式模塊進行解耦分離不確定性，每個子系統模塊可以表達成如下形式:

其中，角標「i」表示第「i」個子系統，xi是子系統si的狀態向量，yi是子系統si的輸出，

將未知項模型不確定項gi(θi)、耦合項以及θ定義如下；

其中q1代表關節位置，λ代表末端約束力，是慣性矩陣，是離心力和哥氏力項，表示重力項，fi表示摩擦力項，zi表示關節之間耦合項；

第二步，設計子系統的非奇異終端滑模函數si

式中，αi，βi，pi，vi，ki和li為待定參數，0＜pi/vi＜1，ki/li＞pi/vi；

第三步，根據第一步建立的狀態空間表達式，通過rbf神經網絡模塊來分別補償其中的未知項、模型不確定項和耦合項，

則未知項模型不確定項gi(θi)和耦合項的rbf神經網絡估計值的表達式如下：

其中，為權值估計誤差，φ(·)為標準rbf神經網絡基函數，為φ(·)的估計值；

由此可得，未知項、模型不確定項和耦合項的形式如下：

第四步，通過第一步、第二步及第三步中給出的狀態空間分離項，非奇異終端滑模函數，以及通過rbf神經網絡估計項，設計面向約束的可重構機械臂系統非奇異終端滑模力位置控制器如下：

τic＝disgn(si)(27)

其中，為期望位置的二階導數，σi為待定正常數，di是所有神經網絡估計誤差的上界，|εf+εh+εgτi|≤di；

最後，通過調節控制器待定參數可以實現軌跡跟蹤精度，同時抑制抖振效應。

本發明的有益效果如下：

1、本發明所述的面向約束的可重構機械臂非奇異終端滑模力位置控制方法有效解決了當末端執行器與外界接觸時，面對特定的任務能夠有效解決可重構機械臂系統力和位置的軌跡跟蹤控制問題。

2、本發明基於非奇異終端滑模技術，實現了軌跡跟蹤誤差值在有限時間內收斂到零，同時改善了誤差趨近律。

3、本發明基於面向約束的可重構機械臂力位置控制方法，不用改變控制器參數的情況下，可以適用於不同的機械臂構形，降低了機械臂的實際應用成本，同時增加了系統可靠性和穩定性。

4、本發明在保證力和位置軌跡跟蹤控制精度的前提下，解決了傳統機械臂控制中由於不確定性等因素引起的控制器抖振問題。

附圖說明

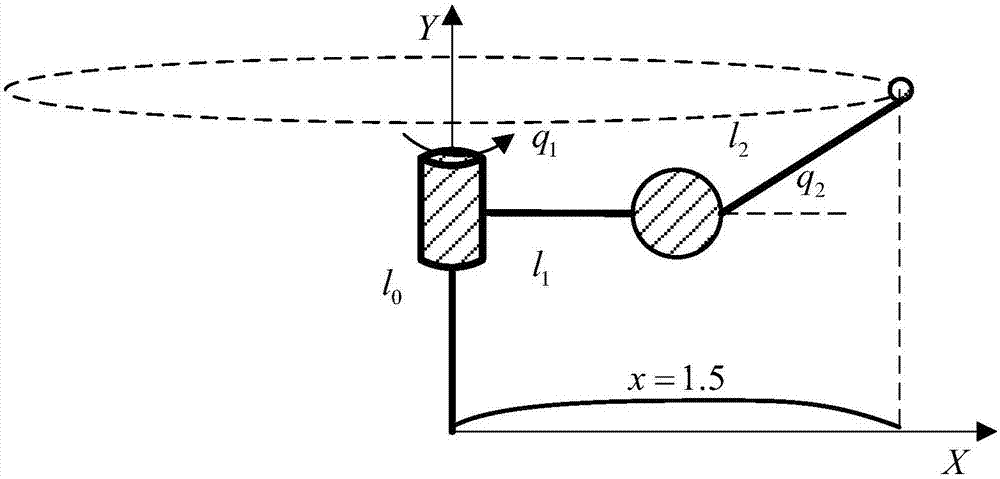
圖1為本發明應用對象之面向約束的可重構機械臂系統構形a的結構示意圖。

圖2位本發明應用對象之面向約束的可重構機械臂系統構形b的結構示意圖。

圖3為本發明面向約束的可重構機械臂非奇異終端滑模力位置控制方法原理圖。

圖4為本發明面向約束的可重構機械臂非奇異終端滑模力位置控制方法流程圖。

具體實施方式

下面結合附圖對本發明進行進一步的詳細說明。

本發明所述的面向約束的可重構機械臂非奇異終端滑模力位置控制方法，普遍適用於集成標準模塊與接口，可以根據不同的任務需求對自身構形進行重新組合與配置的可重構機械臂系統。由於本發明中設計的控制方法適用於多種機械臂構形，因此選擇a、b兩種構形作為示例來闡明該發明所設計的方法的有效性。

如圖1所示，本發明的面向約束的可重構機械臂非奇異終端滑模力位置控制方法應用對象之構形a，為方便說明，構形a是一個二自由度機械臂，約束是一個牆面。機械臂可以在牆面自由運動，均可以取得良好的控制效果。

如圖2所示，本發明的面向約束的可重構機械臂非奇異終端滑模力位置控制方法應用對象之構形b，儘管構形b也是一個二自由度機械臂，但是構形b與構形a的結構形式是完全不同的，約束位置也不同。機械臂可以在約束面內自由運動，可以在不改變控制參數的條件下取得良好的控制效果，從而說明該方法的有效性。

如圖3、圖4所示，面向約束的可重構機械臂非奇異終端滑模力位置控制方法，該方法實現的步驟和過程如下所示：

1、建立面向約束的可重構機械臂系統動力學模型

首先對系統進行初始化，考慮一個n自由度的可重構機械臂工作在一個受約束的環境，並且所受的m維約束可以如下表示：

其中q∈rn是關節位置矢量，是一個二階連續的微分函數。

n自由度面向約束的可重構機械臂系統的動力學方程可以描述成如下公式：

其中分別表示關節速度和加速度矢量，m(q)∈rn×n是慣性矩陣，是離心力和哥氏力矩陣，g(q)∈rn為重力項矩陣，為關節摩擦力項,τ∈rn代表關節力矩矢量，表示由於接觸環境而在在關節坐標中存在的耦合力，其中為帶有約束的雅克比矩陣，λ∈rm是和約束相關的拉格朗日乘子。此外，對於面向約束的可重構機械臂系統，需要滿足如下先驗條件：

條件1、運動約束為無摩擦的剛性約束，而且末端執行器在與接觸約束面始終保持接觸並跟蹤某一預先設定的期望軌跡。

條件2、期望位置和期望的約束力λd是有界的。

條件3、期望約束力的積分項∫λddt及其微分項是已知的。

條件4、可重構機械臂系統的雅克比矩陣是滿秩的。

由於約束的存在，可重構機械臂的操作空間保持(n-m)自由度，因此關節坐標q可以表示成：

其中q2＝σ(q1)，是一個非線性映射函數。

對公式(3)進行時間求導：

其中是一個可逆矩陣，in-m表示單位矩陣，表示σ(q1)對q1的偏導數。

然後對q進行二階求導得到：

把公式(4)和公式(5)帶入公式(2)，面向約束的可重構機械臂系統的動力學方程可以寫成如下形式：

然後，公式(6)通過變換可以寫成

其中

t＝[1…1]t∈rn-m+1

因此，公式(7)的子系統動力學模型可以寫成

其中是慣性矩陣，是離心力和哥氏力項，表示重力項，fi表示摩擦力項，zi表示關節之間耦合項，τi表示子系統力矩項，此外

其中i＝1,2,…n-m+1，當i＝n-m+1時，q1i∈q1。在當前系統中，力控制和所有的關節信息均相關，位置控制只與局部關節信息有關。

定義然後每個子系統都可以描述如下狀態方程的形式

其中xi是子系統si的狀態矢量，yi是子系統si的輸出，並且

2、設定跟蹤誤差並設計非奇異終端滑模函數

根據條件2和3，定義qd為期望的關節位置，λd是期望的受約束的拉格朗日乘子，為期望的約束力。控制目的是使機械臂關節與末端執行器在有限的誤差範圍內能夠跟蹤期望的位置和約束力並且保證閉環系統的穩定性，即達到目標q→qd，λ→λd。

定義軌跡跟蹤誤差如下：

ei＝xi-yid(10)

其中，yid是期望的位置。

定義ei的時間導數如下：

設計第i個子系統的非奇異終端滑模函數

其中αi＞0，βi＞0，pi，vi，ki和li都是待定正常數，且0＜pi/vi＜1，ki/li＞pi/vi。

通過結合公式(9)和公式(11)，得到公式(12)的時間導數為

3、rbf神經網絡補償子系統相關項

通過該部分的發明內容，將公式(9)中的gi(θi)分別通過rbf神經網絡來補償。定義rbf神經網絡函數如式(14)、(15)和(16)所示：

其中ωif，ωig和ωih為理想神經網絡權值，φ(·)為標準rbf神經網絡基函數，δεif、δεig、δεih均表示對應的估計誤差。

定義一般形式神經網絡權值如下形式：

在公式(17)，(18)和(19)中，u和d是θ和的最合適的閉集合。和分別是和gi(θi,ωig)的估計值，其分別可以寫成如下形式

其中是的估計值，權值估計誤差為定義為hi(θi,ωih)的估計值，被用來估計耦合關聯項，如下表示

其中是ωih的估計值，權值估計誤差為

定義公式(9)中的各項如下

其中εf、εg、εh均表示對應的相關估計誤差。

4、設計面向約束的可重構機械臂系統非奇異終端滑模力位置控制器

結合公式(20)、(21)和(22)，所設計的面向約束的可重構機械臂非奇異終端滑模力位置控制器可以寫成如下表達式

τic＝disgn(si)(27)

其中，為標準符號函數，di表示全局神經網絡估計誤差上界，即|εf+εh+εgτi|≤di。

rbf神經網絡的自適應更新率可以定義如下

其中γif，γig，γih都是正常數。

表1控制器參數

然後，通過將控制器參數調整到如上表所示，控制器在整個運行過程中保證了力和位置的跟蹤精度的同時，也有效抑制了抖振效應，此控制器適用於不同的構形的面向約束的可重構機械臂系統而不需要改變任何參數。

最後，將設計的控制器通過matlab軟體來對位置、力、控制力矩進行仿真，通過判斷運行時間是否到達規定時間，若超過規定時間，仿真結果存儲為m文件的形式，輸出結果後結束；若未超過，則繼續轉至解微分方程部分運行。