基於隱馬爾可夫模型的NPC光伏逆變器的故障診斷方法與流程
2023-05-14 23:04:01 1
本發明屬於電力電子運用與故障診斷技術領域,具體涉及基於隱馬爾可夫模型的NPC光伏逆變器的故障診斷方法。
背景技術:
在當前環境形勢日益嚴峻、資源日趨匿乏的情況下,調整能源比重、開發和利用清潔型能源逐漸發展為世界各國能源戰略的重中之重。在對太陽能的各種開發利用中,以在光伏發電技術領域的應用最為常見也最為有價值。
現代控制技術在光伏發電領域中得到了廣泛應用,促使光伏發電控制技術的發展逐漸龐大起來,越來越複雜。在對生產的費用進行降低的同時提升了其效率,同時自動化程度的增長也加大了控制系統故障出現的概率。光伏發電系統的電源動力和控制系統一般有大功率逆變器擔當,逆變器若出現故障而得不到技術的診斷與修復,定會造成無法挽回的經濟損失和安全風險。達到冗餘與容錯控制及平穩運行是光伏發電系統對其所用逆變器進行考察的主要指標。對其安全與平穩運行的保證是光伏發電技術函需處理的重要問題,其在現實應用中的意義非常重大。所以研究光伏逆變器的故障診斷技術就表現得尤為關鍵。
當前較為傳統的NPC逆變器故障診斷方法有基於信號處理的方法和基於知識的方法等,其中基於信號處理的方法雖使用方便,但是其故障特徵的判別參數需要根據專家的經驗來設定,這個缺點降低了此方法的實用性;基於知識的方法雖提高了故障診斷的時效性,但識別正確率較低,有很大的局限性。
技術實現要素:
為解決現有技術存在的問題,本發明提出了一種基於隱馬爾可夫模型的NPC光伏逆變器的故障診斷方法,解決傳統逆變器故障診斷中識別率低及診斷速度慢的問題。
本發明是通過以下技術方案實現上述技術目的的。
基於隱馬爾可夫模型的NPC光伏逆變器的故障診斷方法,其特徵在於,包括以下步驟:
S1,由獲得的NPC光伏逆變器的輸出電壓U、輸出電流I訓練隱馬爾可夫模型,具體過程如下:
S1.1,獲得用於訓練隱馬爾可夫模型的NPC光伏逆變器的輸出電壓U和輸出電流I,包括所有已明確故障類型及正常狀態時的NPC光伏逆變器的輸出電壓U和輸出電流I;
S1.2,對S1.1獲得的所有故障狀態時的輸出電壓U和輸出電流I進行處理;
S1.3,建立一個隱馬爾可夫模型:λ=(π,A,B),確定λ模型中的參數初始值;
S1.4,用Viterbi算法求λ模型的狀態序列;
S1.5,根據S1.4求得的狀態序列求取λ模型的觀測值概率矩陣B;
S1.6,對λ模型進行參數重估使觀測序列的概率最大,得到重估後的參數初始值;
S1.7,得到初始參數後,用Baum-Welch算法對參數進行迭代,直到參數收斂到設定的範圍內;
S2,由某一故障狀態時的輸出電壓U和輸出電流I,對NPC光伏逆變器的故障進行診斷,具體過程如下:
S2.1,根據S1完成訓練後的參數,可以得到對應於NPC光伏逆變器各故障狀態時的隱馬爾可夫模型;
S2.2,將待測故障狀態中的輸出電壓U與輸出電流I用S1.2的方法處理後,帶入S2.1中各故障狀態時的隱馬爾可夫模型;
S2.3,比較各故障狀態時的隱馬爾可夫模型的概率輸出值;
S2.4,概率輸出值最大的模型所對應的狀態為當前NPC光伏逆變器所處的故障。
進一步,S1.1中在訓練隱馬爾可夫模型時,使用對應狀態的NPC光伏逆變器的輸出電壓U和輸出電流I。
進一步,S1.1中用於訓練隱馬爾可夫模型的輸出電壓U和輸出電流I的數值,即可以是離線的數據,也可以是在線監測的數據。
進一步,所述S1.2具體為:
將獲得的輸出電壓U和輸出電流I轉化為離散數值:將輸出電壓U和輸出電流I的幅值等分為多個區域並升序排列,將各區域映射為各個離散值,在此基礎上確定獲得的輸出電壓U和輸出電流I對應的離散數值。
進一步,S1.3具體為:
基於電路的模型,選擇無跳躍的左右型的隱馬爾可夫模型,初始狀態概率π設置為π=[1 0 0 0],狀態轉移矩陣A設置為觀測值概率矩陣B用混合高斯概率密度函數來表示,即其中M是混合高斯概率密度函數的混合數目,cjm是第j狀態時第1個混合高斯的權,μ為正態高斯概率密度函數,Ot為每個故障狀態時的觀測值,ujm為第j狀態時第1個混合高斯元的均值矢量,Ujm表示第j個狀態時第1個混合高斯元的協方差矩陣。
本發明的有益效果為:隱馬爾可夫模型是含有隱藏狀態和觀測狀態的模型,可以解決NPC光伏逆變器故障診斷問題,能很好地處理動態過程;用Viterbi算法求λ模型的狀態序列並建立模型的速度較傳統建模方式更為快捷,經過Baum-Welch算法對參數進行反覆迭代得到的是局部最優解,因此故障識別率非常高。
附圖說明
圖1為本發明使用的隱馬爾可夫模型示意圖;
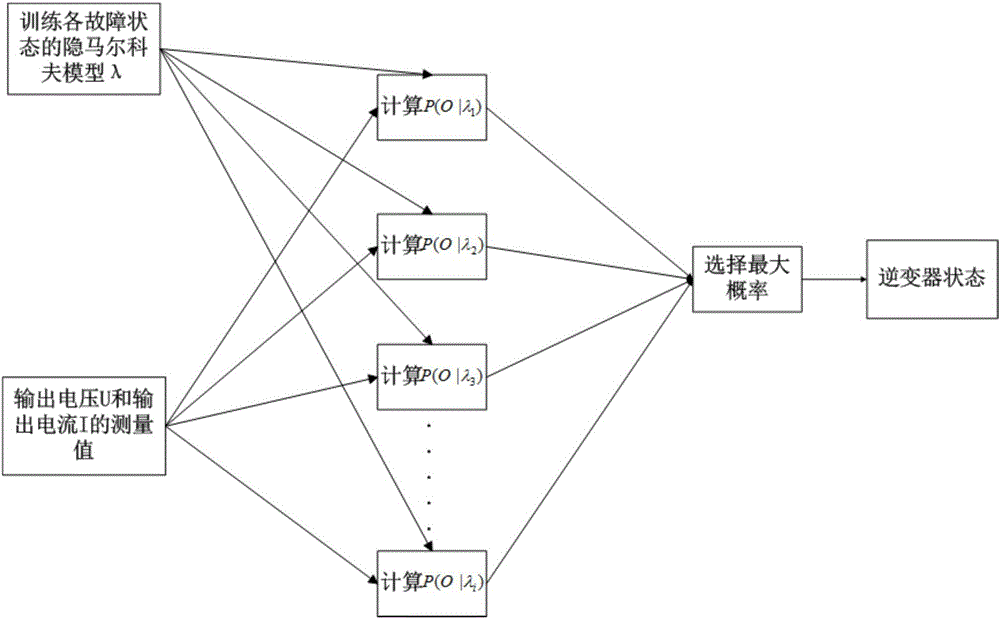
圖2為本發明基於隱馬爾可夫模型的NPC光伏逆變器的故障診斷流程圖;
圖3為本發明隱馬爾可夫模型參數訓練流程圖。
具體實施方式
下面結合附圖及具體實施例對本發明的技術方案進行詳細說明,但本發明的保護範圍並不限於此。
隱馬爾可夫模型HMM是一種統計模型,它用來描述一個含有隱含未知參數的馬爾可夫過程。隱馬爾可夫模型創立於20世紀70年代,80年代得到了傳播和發展,成為信號處理的一個重要方向,現已成功地用於語音識別、行為識別、文字識別以及故障診斷等領域。
隱馬爾可夫模型則是雙重隨機過程,不僅狀態轉移之間是個隨機事件,狀態和輸出之間也是一個隨機過程。
隱馬爾可夫模型有五個基本要素,即一個五元組{N,M,π,A,B}:
其中,N:模型中隱含的狀態個數,N個狀態用θ1,θ2,…θN表示,某一時刻的狀態qt∈(θ1,θ2,…θN),如圖1所示;
M:各狀態對應的觀測值數目,M個觀測值可以用v1,v2,v3…vM表示,某一時刻的觀測值ot∈(v1,v2,v3…vM),如圖1所示;
π:初始狀態概率矩陣,π∈{πi},其中:πi=P(qt=θi)1≤i≤N;
A:轉移概率矩陣,A={aij},其中:aij=P(qt+1=θj,qt=θi)1≤i,j≤N;
B:觀測值概率矩陣,B={bj(k)},其中:bj(k)=P(ot=vk,qt=θj)1≤j≤N,1≤k≤M。
為簡便,HMM簡記為λ=(π,A,B)。
HMM可以解決的三個基本問題:a)評估問題:給定觀察序列o和模型λ,如何快速地計算給定模型的條件下觀察序列的概率;b)解碼問題:給定一個觀察序列o和模型λ,怎樣尋找某種意義上最優的隱狀態序列;c)訓練問題:即HMM的模型參數未知,如何調整這些參數以使觀測序列的概率儘可能的大。
如圖2所示,基於隱馬爾可夫模型的NPC光伏逆變器的故障診斷流程圖,包括步驟:
S1,由獲得的NPC光伏逆變器的輸出電壓U、輸出電流I訓練隱馬爾可夫模型,如圖3所示,具體過程如下:
S1.1,獲得用於訓練隱馬爾可夫模型的NPC光伏逆變器的輸出電壓U和輸出電流I,包括所有已明確故障類型及正常狀態時的NPC光伏逆變器的輸出電壓U和輸出電流I;在訓練隱馬爾可夫模型時,使用對應狀態的NPC光伏逆變器的輸出電壓U和輸出電流I;用於訓練隱馬爾可夫模型的輸出電壓U和輸出電流I的數值,即可以是離線的數據,也可以是在線監測的數據。
S1.2,對S1.1獲得的所有故障狀態時的輸出電壓U和輸出電流I進行處理;
將獲得的輸出電壓U和輸出電流I轉化為離散數值:將輸出電壓U和輸出電流I的幅值等分為多個區域並升序排列,將各區域映射為各個離散值,在此基礎上確定獲得的輸出電壓U和輸出電流I對應的離散數值,即可得到每個故障狀態的觀測值ot=[U,I]。
S1.3,建立一個隱馬爾可夫模型:λ=(π,A,B),確定λ模型中的參數初始值,即狀態數、初始狀態概率、狀態轉移矩陣;
基於電路的模型,選擇無跳躍的左右型的隱馬爾可夫模型,隱含狀態設為4,初始狀態概率π設置為π=[1 0 0 0],狀態轉移矩陣A設置為:
確定觀測值概率矩陣B:
參照設定的隱含狀態個數,將NPC光伏逆變器的輸出電壓U和輸出電流I值均勻分割成N份,時間T=600s,觀測值概率矩陣B用混合高斯概率密度函數來表示,即
其中M是混合高斯概率密度函數的混合數目,本發明M=2,cjm是第j狀態第1個混合高斯的權,μ為正態高斯概率密度函數,Ot為每個故障狀態時的觀測值,ujm為第j狀態時第1個混合高斯元的均值矢量,Ujm表示第j個狀態時第1個混合高斯元的協方差矩陣。
S1.4,用Viterbi算法求λ模型的狀態序列;
定義一個變量δt(i),它表示t時刻沿著路徑q1,q2,q3,…qt,此時qt=θi(i=1,2,3…N),生成觀察序列O1,O2,O3…Ot的最大概率;
所以
求最優狀態序列Q*的過程如下:
①初始化,t=1時:
δ1(i)=πibi(o1),1≤i≤N (4)
其中,bi=bj(k);是迭代次數,這裡將其初始化;
②遞歸
δt(i)=max1≤i≤N([δt-1(i)aij])bj(ot),2≤t≤T,1≤j≤N (6)
其中,argmax表示:如果i=I,f(i)達到最大值,則定義I是輸出電流大小,f(i)=δt-i(i)aij;
③終結
P*=max1≤i≤N[δT(i)] (8)
qT*=argmax1≤i≤N[δT(i)] (9)
其中,P*是最大的δt(i),qT*是概率為δt(i)時的序列;
④最佳狀態序列求解
其中,q均為狀態序列,為迭代次數;
S1.5,根據S1.4求得的狀態序列求取λ模型的觀測值概率矩陣B。
S1.6,對λ模型中的π、A、B進行參數重估使觀測序列的概率最大,得到重估後的參數初始值
定義一個變量ξt(i,j),表示在觀測序列O和模型λ存在的條件下,隱馬爾可夫模型在t時刻處於θi狀態且在t+1時刻處於θj的概率,即
ξt(i,j)=P(O,qt=θi,qt+1=θj|λ) (11)
進一步可得
ξt(i,j)=[αt(i)aijbj(ot+1)βt+1(j)]/P(O|λ) (12)
其中,bj(ot+1)=bj(k),αt(i)為定義的前向變量,
αt(i)=P(o1,o2,…,ot,qt=θt|λ) (13)
βt+1(j)是定義的後向變量
βt+1(j)=P(ot+1,ot+2,…,oT|qt=θt,λ) (14)
所以馬爾可夫模型在t時刻處於狀態θi的概率為
其中,表示狀態由θi轉移到θj的期望值數目,βt(i)為後向變量;
重估公式為:
得到重估後的初始參數
S1.7,得到初始參數後,用Baum-Welch算法對參數進行迭代,直到參數收斂到設定的範圍內;
由求不斷用此算法迭代,直到預先設定的收斂範圍,此時即為訓練完成的馬爾可夫模型,求P(O|λ)得方法為:
定義一個向前變量:
αt(i)=P(O1,O2,O3…Ot,qt=θi|λ),1≤t≤T (19)
其中,αt(i)表示在t時刻隱含狀態序列S=q1,q2,q3,…qT狀態下,生成的部分觀察序列O={O1,O2,O3…Ot}的概率;
①初始化
αt(i)=πibi(o1) (20)
②遞歸
③終結
S2,由某一故障狀態時的輸出電壓U和輸出電流I,對NPC光伏逆變器的故障進行診斷,具體過程如下:
S2.1,根據S1完成訓練後的參數,可以得到對應於NPC光伏逆變器各故障狀態時的隱馬爾可夫模型;
S2.2,將待測故障狀態中的輸出電壓U與輸出電流I用S1.2的方法處理後,帶入S2.1中各故障狀態時的隱馬爾可夫模型;
S2.3,比較各故障狀態時的隱馬爾可夫模型的概率輸出值P(O|λ);
S2.4,概率輸出值最大的模型所對應的狀態為當前NPC光伏逆變器所處的故障。
以上實施例僅用於說明本發明的設計思想和特點,其目的在於使本領域內的技術人員能夠了解本發明的內容並據以實施,本發明的保護範圍不限於上述實施例。所以,凡依據本發明所揭示的原理、設計思路所作的等同變化或修飾,均在本發明的保護範圍之內。
