一種基於斯坦納樹的配電網規劃方法與流程
2023-04-27 17:11:07 2
本發明屬於輸電系統規劃建設技術領域,具體涉及一種基於斯坦納樹的配電網規劃方法。
背景技術:
配電網是處於電力系統末端的起重要分配電能作用的網絡,直接向用戶供電,所以配電網是整個電力系統的重要組成部分。對配電網進行合理、科學的規劃,可以保證電網運行的經濟性和安全性,提高用戶的供電質量。配電網規劃是根據規劃期間負荷預測的結果和現有的網絡結構,確定最優的網絡建設方案,在滿足負荷需求和高質量電能的前提下,使得配電網的建設和運行費用最小。但不確定性分布式電源的接入,給配電網規劃帶來新的挑戰。
分布式電源(Distributed Generation,DG)是接在用戶附近或配網中的小型發電設備,它能夠使風、光等清潔能源和分散小火電、小水電等形式能源得到充分利用,緩解能源危機。隨著相關支持政策的出臺,配網中DG滲透率逐年升高,含DG的配電網規劃研究就顯得刻不容緩。配電網規劃是帶有約束條件的非線性混合整數優化問題,DG的加入使規劃維數和計算難度都大大增加。因此簡單易用的含有DG的配電網規劃模型的研究就十分必要。
目前,常見的含分布式電源配電網規劃模型有基於啟發式、數學規劃、隨機優化的協調規劃模型。啟發式協調規劃模型應用比較方便,但無法保證結果的最優性。數學規劃協調規劃模型雖可保證結果的最優性,但無法逃避隨著求解規模的增大算法難收斂的問題。隨機優化協調規劃模型可以求解規模較大的規劃問題,但是很容易陷入局部最優解。所以,基於求解算法的局限性,目前還沒有一種簡單易用、較好的適用於目前求解算法工具的含有分布式電源配電網規劃模型。
技術實現要素:
針對背景技術存在的問題,本發明提出了一種基於斯坦納樹的配電網規劃方法,該方法充分考慮了DG出力因素,消除了DG對配電網規劃的影響,降低了配電網規劃的維度和求解難度。
為解決上述技術問題,本發明採用如下的技術方案:
一種基於斯坦納樹的配電網規劃方法,包括步驟:
步驟1,將配電網中節點分為源節點、負荷節點和互聯節點,並構建無向圖G=(V,E),V=Vs∪Vd∪Vt,Vs為源節點集,Vd為負荷節點集,Vt為互聯節點集,E為支路集;
步驟2,以源節點和負荷節點為必須連接的點、互聯節點為斯坦納點,根據求取對象類型構建邊加權的斯坦納樹模型或點加權的斯坦納樹模型,基於配電網的等年值費用獲得線路或節點的等年值費用,即斯坦納樹模型的邊權值或點權值;
所述的線路的等年值費用為線路建設和運行的等年值費用、線路有功損耗的等年值費用、線路停電損耗的等年值費用和線路DG用電獎勵因子之和,其中,線路DG用電獎勵因子為Cr為DG發電獎勵因子,S1、S2、…Sn分別為DG節點連接線路的線路容量;
所述的節點的等年值費用是將線路建設和運行的等年值費用、線路有功損耗的等年值費用、線路停電損失的等年值費用按照線路兩端節點容量分攤到兩端節點,即獲得節點建設和運行的等年值費用、節點有功損耗的等年值費用、節點停電損失的等年值費用;節點DG發電獎勵因子即所連接DG的DG發電獎勵因子,未連接DG的節點的DG發電獎勵因子即為0;
步驟3,採用基於自適應學習的粒子群法求解斯坦納樹模型,獲得邊權值和或點權值和最小、且滿足潮流約束的斯坦納最小生成樹,即最優規劃。
步驟2中,將線路建設和運行的等年值費用、線路有功損耗的等年值費用、線路停電損耗的等年值費用按照線路兩端節點容量分攤到兩端節點,具體為:
使線路兩端節點對應的費用之和為線路對應的費用,且線路兩端節點的費用之比等於兩端節點容量之比。
例如,假設線路Li,j的建設和運行的等年值費用為Z,線路Li,j兩端節點i、j的容量為si、sj,則節點i的建設和運行的等年值費用為
步驟2中,若求取對象類型為網架規劃,則構建邊加權的斯坦納樹模型;若求取對象類型為電源規劃或負荷規劃,則構建點加權的斯坦納樹模型。
步驟3進一步包括子步驟:
3.1設置最大迭代次數,初始化粒子群位置和速度,計算初始狀態下由斯坦納點組合的最小生成樹,以該最小生成樹為當前最優解;
3.2根據預設規則更新粒子群位置和速度;
3.3計算當前狀態下由斯坦納點組合的最小生成樹,判斷當前最小生成樹對應的權值和是否小於當前最優解的權值和;如果不小於,執行步驟3.2;否則,執行步驟3.4;
3.4對當前最小生成樹進行潮流計算,檢驗當前最小生成樹是否滿足潮流約束;如果不滿足潮流約束,執行步驟3.2;否則,執行步驟3.5;
3.5以當前最小生成樹為當前最優解,並判斷當前迭代次數是否達到最大迭代次數,若達到,當前最優解即最優規劃;否則,執行步驟3.2。
與現有技術相比,本發明具有以下優點和有益效果:
1)本發明基於斯坦納樹的配電網規劃方法簡單易用,在滿足計算精度的情況下能夠適用於大部分隨機優化算法,可以用於含分布式電源的配電網規劃;
2)本發明消除了分布式電源對配電網規劃的影響,引入DG獎勵因子並將其加到斯坦納樹權值中,在節約資源以及促進可持續發展的同時,降低了配電網規劃的維度和求解難度。
附圖說明
圖1為斯坦納樹示例圖,其中,圖(a)為待求解的斯坦納樹網絡,圖(b)為求解的最小斯坦納樹網絡;
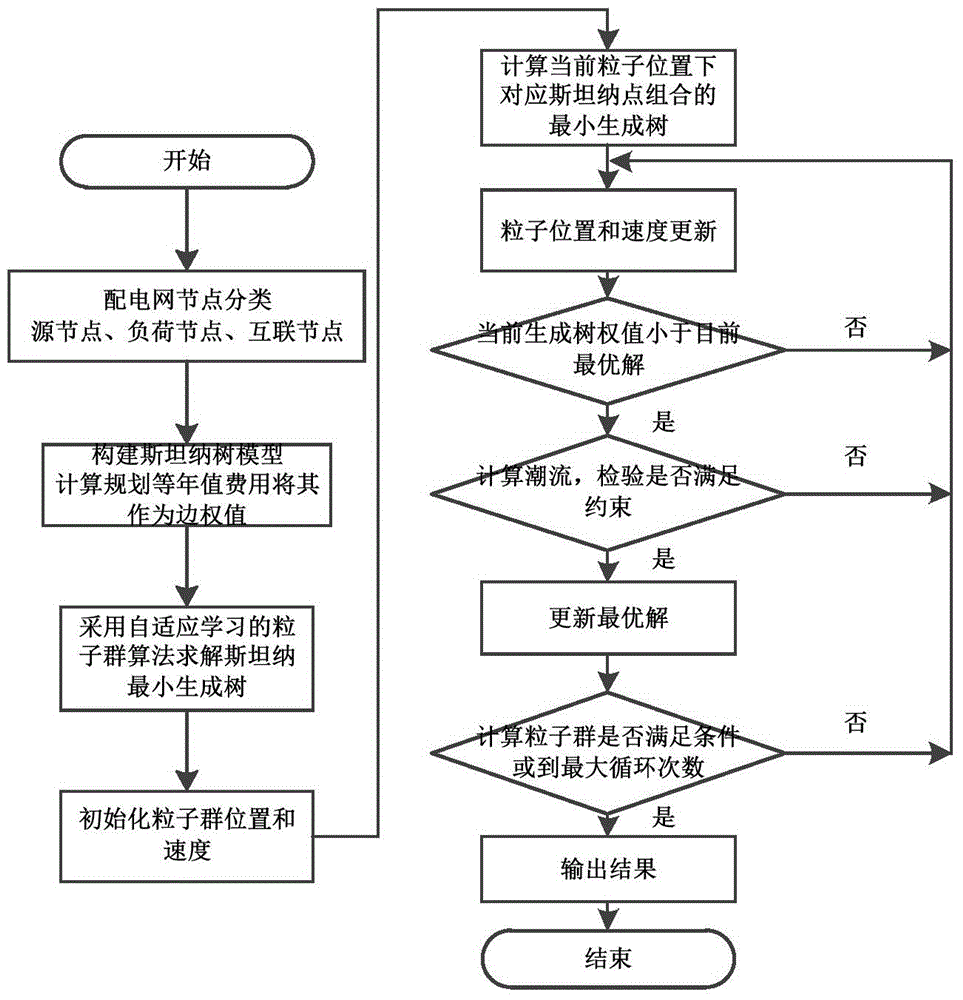
圖2為本發明的具體流程圖;
圖3為實施例中可規劃線路結構圖;
圖4為實施例中獲得的最優規劃網絡圖。
具體實施方式
下面將結合附圖和具體實施方式進一步說明本發明技術方案。
本發明具體步驟如下:
步驟1,配電網節點的分類。
將配電網中節點分為源節點、負荷節點和互聯節點三類。源節點是配電網和輸電網的公共連接點,是配電網的電源點。負荷節點是接有負荷的節點,它為負荷直接提供能量。實際配電網中,負荷客戶或者二級網絡的母線節點均歸類為負荷節點。待建設的節點或者規劃中可以利用的非負荷節點均歸類為互聯節點;
步驟2,構建無向圖。
根據配電網節點的分類,構建無向圖G=(V,E),V=Vs∪Vd∪Vt,Vs是源節點集,Vd是負荷節點集,Vt是互聯節點集,E是支路集。
步驟3,基於斯坦納樹劃分各節點屬性。
無向圖G中Vs和Vd是求解最小斯坦納樹中必須連接的點,互聯節點Vt為斯坦納樹模型中的斯坦納點,是可連可不連的備選連接點。
步驟4,根據求取對象類型選擇斯坦納樹模型,基於配電網的等年值費用獲得斯坦納樹模型權值。
斯坦納樹模型包括邊加權的斯坦納樹模型和點加權的斯坦納樹模型,根據求取對象類型進行選擇。如求取對象為網架規劃,則選擇邊加權的斯坦納樹模型;如求取對象為電源規劃或負荷規劃,則選擇點加權的斯坦納樹模型。
配電網的等年值費用包括線路建設和運行費用的等年值費用、有功損耗費用、停電損失費用和DG發電獎勵因子之和。
單位長度線路的建設和運行費用c1為:
c1=c0+c2[|i|2rτ] (1)
式(1)中,c0是單位長度線路年建設費用;c2為電價;r為單位長度線路電阻;τ為年運行時間;i為線路電流。
將線路的建設和運行費用c1轉換為對應的等年值費用Z1:
<![CDATA[ Z 1 = Σ L i , j L r 0 ( 1 + r 0 ) T ( 1 + r 0 ) T - 1 c 1 l i , j - - - ( 2 ) ]]>
式(2)中,r0為投資折現率;T為投資的回收年限;L表示支路集,li,j表示由節點i、j構成的線路Li,j的長度。
線路Lj,k的有功損耗Δpj,k為:
式(3)中,Ij,k為連接j、k節點線路Lj,k的電流;Rj,k為連接j、k節點線路Lj,k的電阻。
線路有功損耗的等年值費用即線路有功損耗Δpj,k與年電費的乘積。
停電損失費用為:
式(4)中,λ為單位長度線路故障率;c3,j為j節點的停電損失費用,由用戶提供;為連接i、j節點線路Li,j的有功功率。
含有DG的配電網規劃中,增加分布式電源的DG獎勵因子作為罰單元,體現分布式電源的環境效應和配電網對分布式電源的接納能力。
DG獎勵因子Cr如下:
<![CDATA[ C r = α ( Σ q Q P DG , q ) - - - ( 5 ) ]]>
式(5)中,α為獎勵係數,為生產單位電能傳統能源產生汙染的治理成本減去分布式電源產生汙染的治理成本之差;PDG,q為q節點的DG有功功率,q節點即與DG連接的節點,Q表示與DG相連的節點集。
步驟6,用基於自適應學習的粒子群法求解斯坦納最小生成樹。
斯坦納樹問題是組合優化問題,與最小生成樹相似,是最短網絡的一種。最小生成樹是在給定的點集和邊中尋求最短網絡使所有點連通。而最小斯坦納樹允許在給定點外增加額外的點,使生成的最短網絡開銷最小。本發明粒子群法基於「搜索結合調整」的思想先計算線路等年值費用,將其作為邊權值,並以電源節點、負荷節點分別為起點和終點計算斯坦納樹,再驗算其潮流是否滿足,對於不滿足約束的線路進行修正,最終得到滿足約束條件的斯坦納樹。並與遺傳算法、基本粒子群算法的20次求解結果所得尋優次數進行對比。
本步驟具體過程如下:
(1)設置迭代次數,初始化粒子群位置和速度。
(2)計算初始狀態下斯坦納點組合的最小生成樹,以該最小生成樹為當前最優解。
(3)更新粒子群位置和速度。
(4)計算當前狀態下斯坦納點組合的最小生成樹,判斷當前最小生成樹對應的權值和是否小於當前最優解的權值和;如果不小於,轉到步驟(3);如果小於,執行步驟(5)。
(5)對當前最小生成樹進行潮流計算,檢驗當前最小生成樹是否滿足潮流約束。如果不滿足潮流約束,轉到步驟(3);若滿足潮流約束,則進行步驟(6)。
(6)以當前最小生成樹為當前最優解,判斷當前迭代次數是否達到最大迭代次數,若未達到,轉到步驟(3);否則,進行步驟(6)
(7)保存當前最優解,即最優規劃。
下面通過具體案例說明本發明。
以某地區54節點配電網為例,該配電網中共有97條可規劃線路,結構如圖3。採用基於自適應學習的粒子群法求解斯坦納樹模型,並與遺傳算法和基本粒子群求取結果進行對比。
步驟1,將54節點配電網算例中的節點進行分類,根據類型需要分類結果為源節點1個、負荷節點33個、互聯節點20個。
步驟2,根據可規劃的線路以及節點分類情況構建無向圖G=(V,E),支路集E即圖3中虛線構成的集合。
步驟3,基於斯坦納樹劃分各節點屬性,源節點和負荷節點是必須連接的節點,互聯節點是可連可不連的備選點。見圖3,源節點用黑色方塊表示,負荷節點用黑色圓圈表示,互聯節點(斯坦納點)用白色圓圈表示。
步驟4,由於考慮到涉及配電網的網架規劃以及計算的物理意義和簡潔性,選用邊權值的斯坦納樹模型,並將配電網規劃的等年值費用作為斯坦納樹的邊權值進行計算。
斯坦納樹的邊權值(即配電網每條規劃線路的等年值費用)為線路建設和運行的等年值費用、線路有功損耗的等年值費用、線路停電損耗的等年值費用和線路/節點的DG發電獎勵因子。根據DG發電獎勵因子Cr,按照與DG相連的線路容量分布獲得各線路上DG發電獎勵因子,具體為:DG節點連接n條線路l1、l2、…ln,對應的線路容量分別為S1、S2、…Sn,則線路lk的DG發電獎勵因子為
步驟6,用基於自適應學習的粒子群法求解斯坦納最小生成樹,求得最優網絡,見圖4,並與遺傳算法、基本粒子群算法的20次求解結果所得尋優次數進行對比。對比結果如表1所示,其中,CLSPSO表示本發明方法,GA為遺傳算法,PSO為基本粒子群算法。
表1CLSPSO、GA、PSO 20次尋優結果
3種算法20次優化結果呈現一定程度的波動性,CLSPSO優化算法標準差最小,說明波動性最小,穩定性較強。3種算法都能搜索到最優解,CLSPSO優化算法搜索到最優解次數遠高於另外2種算法,搜索效率較高,全局搜索能力較強。但3中算法20次搜索中搜到最優解的次數都不算低,這也說明了該模型不僅簡單易用,而且對各種隨機優化算法都有一定的適應性。
本文中所描述的具體實施例僅僅是對本發明精神作舉例說明。本發明所屬技術領域的技術人員可以對所描述的具體實施例做各種各樣的修改或補充或採用類似的方式替代,但並不會偏離本發明的精神或者超越所附權利要求書所定義的範圍。
