基於偏差分離的狀態反饋線性控制方法與流程
2023-09-15 14:22:30 1
本發明涉及自動化控制領域中的控制系統設計方法,具體是涉及一種基於偏差分離的狀態反饋線性控制方法。
背景技術:
在工程實際中,不確定性與非線性普遍存在於被控系統中。為了解決不確定性與非線性對被控系統造成的影響,常用的控制方法主要有兩大類:第一大類方法即魯棒控制方法,採用不確定性界的信息來參與控制器設計。然而,由於不確定性界的信息在工程實際中很難準確獲取,系統設計往往採用「最壞情況」進行界的估計,這導致魯棒控制方法的保守性。另一大類方法是各種自適應控制方法,通過對不確定性的逼近或估計來及時修正控制器的參數,使得控制系統穩定和保持期望的控制性能。這類方法常常假定不確定性有界,所得到的控制結構與算法也相當複雜。
技術實現要素:
本發明通過現有技術的不足,提供一種基於偏差分離的狀態反饋線性控制方法;該方法不僅能夠補償不確定性與非線性對被控系統造成的影響,而且設計出的控制結構與算法簡單,操作方便。
基於偏差分離的狀態反饋線性控制方法,其主要按照以下步驟進行:
首先,考慮不確定非線性系統:
其中,x(t)∈Rn,u(t)∈Rm(m≤n)與w(t)∈Rp分別為該系統的狀態變量、控制輸入以及外部擾動;假定x=0是系統(1)的平衡點,在實際工程設計中,系統(1)在x=0附近可分成兩部分:用線性微分方程描述的主體部分與模型偏差部分,即系統(1)重寫為
其中,A∈Rn×n,B∈Rn×m為已知的常值矩陣,D(x,u,w)∈Rn為模型偏差,該模型偏差包括系統的非線性與不確定性;不失一般性,假定{A,B}能控;
其次,提出線性控制結構:
u(t)=u0(t)+ue(t) (3)
式中,u0(t)=Kx,其中K的選取使得矩陣Ak(=A+BK)的全部特徵值均具有負實部;其中Δ>0,矩陣η1,η2∈Rn×m的選取使得||Bue+D(x,u,w)||儘量小;
再次,設計控制器,對於若存在L1,L2∈(0,β),且β2>eL1(L1+L2),並滿足下列條件:
i)||D1(x1,u,w,t)-D1(x2,u,w,t)||≤L1||x1-x2||
ii)||D2(x1,u,w,t)-D2(x2,u,w,t)||≤L2||x1-x2||,
則控制器(3)使得系統(2)在平衡點x=0上的指數漸近穩定,其中,Δ∈[0,-L1β-2+β-1ln[β2/L1(L1+L2)]),β=max{-Re(λi),i=1,2,…,n},λi為Ak的特徵值。
本發明通過構造觀測器在線獲取被控對象模型偏差的信息,進而設計簡單的線性控制結構補償不確定性與非線性帶來的影響。相比於傳統的控制方法,本發明不僅給出一種控制系統設計方法,能夠設計出簡單的控制結構與算法,還可以減少甚至抵消不確定性與非線性的影響,滿足快速性、可實現性和高可靠性方面的要求,具有較好的工程意義。
附圖說明
圖1為基於偏差分離的狀態反饋線性控制原理圖;
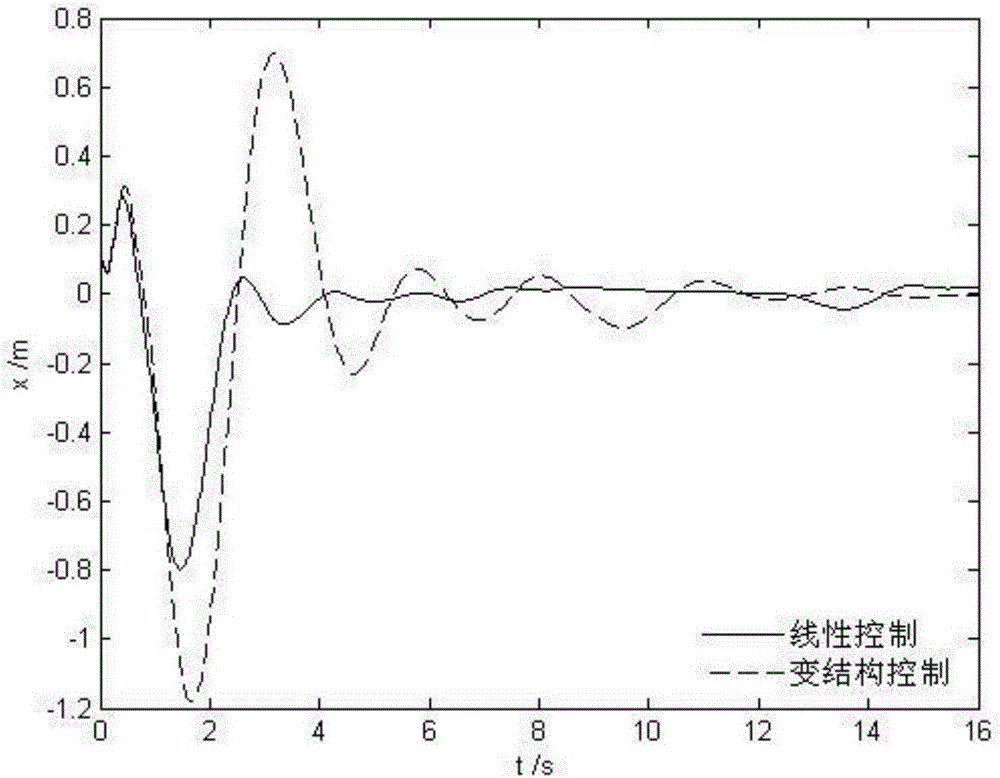
圖2為系統狀態變量x的仿真結果圖;
圖3為系統狀態變量φ1的仿真結果圖;
圖4為系統狀態變量φ2的仿真結果圖;
圖5為系統狀態變量φ3的仿真結果圖;
圖6為線性控制量u的仿真結果圖;
圖7為變結構控制量u的仿真結果圖。
具體實施方式
以下結合附圖和具體實施例對本發明進行詳細描述,但不作為對本發明的限定。
參照圖1,本發明基於偏差分離的狀態反饋線性控制方法,其主要按照以下步驟進行:
首先,考慮不確定非線性系統:
其中,x(t)∈Rn,u(t)∈Rm(m≤n)與w(t)∈Rp分別為該系統的狀態變量、控制輸入以及外部擾動;假定x=0是系統(1)的平衡點,在實際工程設計中,系統(1)在x=0附近可分成兩部分:用線性微分方程描述的主體部分與模型偏差部分,即系統(1)重寫為
其中,A∈Rn×n,B∈Rn×m為已知的常值矩陣,D(x,u,w)∈Rn為模型偏差,該模型偏差包括系統的非線性與不確定性;不失一般性,假定{A,B}能控;
其次,提出線性控制結構:
u(t)=u0(t)+ue(t) (3)
式中,u0(t)=Kx,其中K的選取使得矩陣Ak(=A+BK)的全部特徵值均具有負實部;其中Δ>0,矩陣η1,η2∈Rn×m的選取使得||Bue+D(x,u,w)||儘量小;
再次,設計控制器,對於若存在L1,L2∈(0,β),且β2>eL1(L1+L2),並滿足下列條件:
i)||D1(x1,u,w,t)-D1(x2,u,w,t)||≤L1||x1-x2||
ii)||D2(x1,u,w,t)-D2(x2,u,w,t)||≤L2||x1-x2||,
則控制器(3)使得系統(2)在平衡點x=0上的指數漸近穩定,其中Δ∈[0,-L1β-2+β-1ln[β2/L1(L1+L2)]),β=max{-Re(λi),i=1,2,…,n},λi為Ak的特徵值。
參照圖1~7,三級倒立擺系統的穩定控制問題:三級倒立擺系統的狀態變量為
式中,x是臺車的位移,φ1,φ2,φ3分別是一擺、二擺和三擺的角度;系統參數如表A:
表A
在X=0附近對倒立擺的非線性模型線性化,可得線性模型如下:
其中Ai為系統常量如表1:
表1
取倒立擺的線性模型作為標稱系統,且系統完全能控,設其期望的閉環極點為:
p=[-3+1.8j,-3-1.8j,-5+0.5j,-5-0.5j,-6,-4,-7,-8];
狀態反饋增益陣為:
K=[-0.6370,-74.4805,132.8565,-75.0797,-3.0985,-1.6322,6.0225,-7.8655];
控制器設計採用線性結構(如式(3))進行仿真分析,其中初始狀態設置為x(0)=0.1m,φ1(0)=0rad,φ2(0)=0.05rad,φ3(0)=-0.02rad,其他狀態的初始值均為零,初始角度變化的穩定範圍見表2。選取系統的ITAE性能指標,
J=∫t(|x|+|φ1|+|φ2|+|φ3|)dt;
來評價系統的動態性能,並與變結構控制進行對比。仿真結果如圖2~7。
表2為初始角度變化的穩定範圍。
表2
仿真研究表明,線性控制中系統狀態的變化幅度較小,過渡過程時間較短,系統狀態能夠快速到達穩態值;相比之下,變結構控制中系統狀態振蕩幅度較大,調節時間較長,各狀態量的振蕩幅度是線性控制的0.5-4倍,調節時間是線性控制的2-3倍。
因此,線性控制系統可以顯著減小系統狀態的變化幅度,縮短過渡過程時間,提高系統響應的快速性,系統的動態性能明顯改善,具有較強的魯棒穩定性。此外,由於線性控制採用線性控制策略,在工程中可以方便地實現,因此在工程實踐中具有廣泛的應用前景。
可見,本發明實施例通過構造觀測器在線獲取被控對象模型偏差的信息,進而設計簡單的線性控制結構補償不確定性與非線性帶來的影響。相比於傳統的控制方法,本發明不僅給出一種控制系統設計方法,能夠設計出簡單的控制結構與算法,還可以減少甚至抵消不確定性與非線性的影響,滿足快速性、可實現性和高可靠性方面的要求,具有較好的工程意義。
以上已將本發明做一詳細說明,但顯而易見,本領域的技術人員可以進行各種改變和改進,而不背離所附權利要求書所限定的本發明的範圍。
