一種微地震地面監測速度模型校正算法的製作方法
2023-06-04 11:11:01 4
本發明涉及一種微地震地面監測速度模型校正算法。
背景技術:
水力壓裂技術在低滲油氣田開發開採以及儲層改造過程中發揮著至關重要的作用,通過水力壓裂技術開發低滲透油氣藏已成為一種普遍趨勢。微地震定位技術是微地震監測工作的核心,該技術實施過程中,裂縫延伸導致周圍巖石破裂,從而引發一系列可觀測記錄的微地震事件。而監測工區範圍內的速度模型是影響微地震事件定位準確與否的主要因素,因此,如何獲得一個有效的速度模型是微地震監測工程中一個關鍵性問題。
在微地震監測工程中,地震層析成像方法是尋求地下速度結構的有效手段,但在實際壓裂監測過程中受條件制約,射孔信息量較少,地面檢波器數量及覆蓋範圍嚴重不足,獲得較為精細的工區地下速度結構幾乎是不可能的。目前現有的微地震速度模型構建方法都以射孔重定位精度作為評判依據。anikiev採用嘗試的辦法,同時對各層測井初始模型進行同時增加或減小一定值,得到一個相對較準確的反演速度模型。pei等採用occam法進行地下速度模型反演,譚玉陽等採用levenberg-marquardt方法進行速度模型反演。pei等,jiang等採用極快速模擬退火方案進行速度模型校正,取得了一定效果。但以上方法均依賴於射孔記錄的初至拾取,在低信噪比情況下該方法失效。
cn105807316a公開了一種《基于振幅疊加的地面觀測微地震速度模型校正方法》,從逆時偏移振幅疊加法原理出發,並結合極快速模擬退火算法,不需要拾取震相初至信息,通過監測射孔點重定位精度,判斷速度模型是否可用於後續微地震定位。能有效的克服現有算法存在的極大值和最大值不分的情況,準確的找到能量聚焦最大值e,準確定位射孔位置,有效的校正速度模型。
但上述方法僅考慮到各層的速度不確定性,而並沒有考慮到各層位位置不確定性,導致射孔重定位仍存在一定誤差。因此,如何有效克服現有的微地震地面速度模型校正缺陷從而進一步提高微地震事件定位精度是本領域亟需解決的問題。
技術實現要素:
為了解決上述問題,本發明在振幅疊加地面觀測微地震速度模型校正方法的基礎上,在極快速模擬退火方法過程中同時考慮各層速度不確定性以及層位不確定性,通過擴大解空間的方法提高射孔事件重定位精度。
實現本發明方法的步驟如下:
a、在地面布置n個檢波器,並以射孔點位置作為中心點定義目標區域;
b、根據定位精度需要將目標區域劃分成若干網格尺寸大小相同的體元;
c、根據測井曲線建立初始速度模型並讀取n個檢波器所獲取的n道地震波資料;
d、採用震幅疊加方法定位射孔體元,並獲得能量聚焦值最大的網格體元中心點坐標及相應能量聚焦值e;
e、以速度值和層位值作為不確定因素,採用極快速模擬退火法對目標層進行調整;
f、對射孔事件進行重定位,如果定位誤差不滿足定位要求,還需進行回火處理調整速度模型,直到定位誤差足夠小為止。
g、是否滿足射孔精度要求:是;
h、結束。
步驟d中震幅疊加方法具體如下:
d1、計算各道檢波器獲取的地震波相對於參考道的走時差δti;參考道選擇有相對清晰的初至同相軸及較高的信噪比;
式(1)表示第i道與參考道走時之差;式(1)中δlij為第i道與參考道在第j層的路徑差,vj第j層的波速;
d2、各道檢波器獲取的地震波波形根據δti逆時偏移後進行震幅疊加,表達式為:
式(2)中,各道波形在第j時刻的振幅值為a(f(t),k);m為檢波器個數,n為時窗長度;k為第j時刻的第k個採樣點;
將式(1)帶入式(2)得到:
其中步驟e,極快速模擬退火法具體實施如下:
第一步,根據測井曲線獲得初始速度向量v,v=[vp1,vp2,vp3,...,vpn]及初始層位模型向量h,h=[h1,h2,h3,...,hm-1],其中,vpi為第i層p波速度,hj為第j個層界面深度坐標。
第二步,計算目標函數e(v),具體計算方法如下:
在測井數據中,選擇任意一道作為參考道m,採用射線追蹤的方法求取其它各道相對於該參考道的理論走時差:
δtcal=[t1-tm,t2-tm,...,tn-tm](4)
根據該理論走時差對各道檢波器獲得的射孔記錄波形進行逆時偏移疊加,目標函數(疊加能量)的數學表達式如下:
其中a為第i個體元在第j時刻的震幅大小,第i個體元的中心點坐標為(xi,yi,zi),m為檢波器個數,n為時窗長度;
第三步,計算模擬退火初始溫度t0,獲取初始溫度的解決方法如下:
先給初始溫度一個很小的正值,然後不斷乘以一個恆大於1的數,直到滿足對任何模型的接受概率接近於1為止;
其中,v0為初始速度模型,v1為第一次迭代模型結果。
第四步,進行模擬退火降溫計算,極快速模擬退火降溫公式如下:
tk=t0exp(-ck1/2n)(7)
其中k為迭代次數,t0為初始退火溫度,c為給定常數用來調整算法退火溫度,這裡c=0.5;n為需要調整速度的層數;
在進行模擬退火計算過程中,還需調整速度向量v和層位模型向量h,具體公式為:
其中,與為各層速度的最大最小邊界值,其中與為各層位最大最小邊界值。其中sgn為符號函數,x為隨機變量,取值範圍在[-1,1]之間。μ∈[0,1];產生x表達式為:
每次迭代計算模擬退火接受概率計算如下:當e(v′)≥e(v)時,v′替代v作為當前最優解,當e(v′)<e(v)時,以概率
替代當前最優解,其中tk為第k次迭代時的溫度值。最後以e(v)>e作為本次模擬退火運算疊代終止條件。
本發明的有益效果:
現有技術中的極快速模擬退火算法過程中僅考慮了各層的速度向量v=(vp1,vp2,vp3,...,vpn)t的不確定性。而並沒有考慮到工區地下層位測量不準而導致的第i道與參考道在第j層的路徑差δlij的不確定性。這就導致速度模型解空間較小,雖經模擬退火運算,但仍無法完全消除射孔重定位誤差。本專利提出在原算法模擬退火計算過程中加入各層位不確定因素,通過增大解空間的方式提高射孔點重定位精度,能夠很好的解決射孔重定位不準的問題,並有效提高射孔點周圍微地震定位可信度。
附圖說明
圖1基于振幅疊加的地面觀測微地震速度模型校正方法流程圖;
圖2二維層狀起伏結構地層模型圖;
圖3檢波器各道正演模擬波形圖;
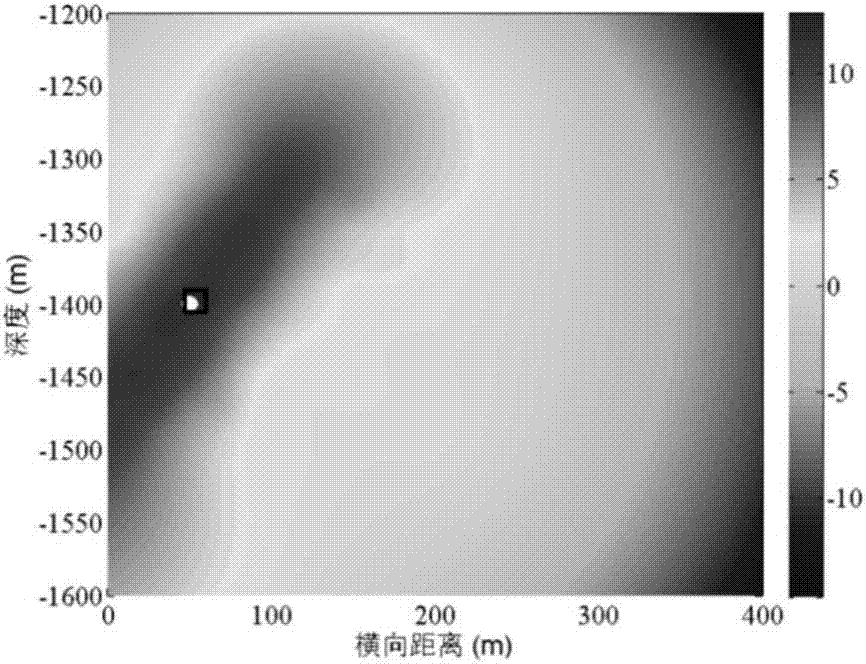
圖4(a)常規振幅疊加算法射孔重定位結果;
圖4(b)算法改進後的射孔重定位結果;
圖5震源定位分布結果;
圖6震源定位誤差結果圖;
圖7(a),(b)為經過本文改進後射孔重定位結果;
圖7(c),(d)為採用常規振幅疊加速度模型校正算法射孔重定位結果。
具體實施方式
實施例1
下面結合附圖和模擬地層模型對本發明技術方案以具體實施例的方式進行清楚、完整的描述。具體實施步驟如圖1所示,具體如下:
a、如圖2所示,選擇二維層狀起伏結構地層模型進行驗證本文的改進算法,實際信號採用有限差分波動方程進行模擬,根據所模擬的地層模型建立初始平層狀地層模型,後續的正演採用射線追蹤方法,反演方法採用上述振幅疊加速度模型校正方法,並加入本文所提出的層位不確定因素,本次實驗假定中間各層位上下浮動不超過50m。檢波器排布與震源位置如圖2所示,其中首個檢波器坐標為(200,0),每個檢波器間距為50m,震源位置為(50,1400)。表1為根據測井曲線建立的初始速度模型參數。圖3為各道檢波器正演模擬波形。
b、將目標區域劃分為網格尺寸為10m的體元,每一個網格中心可以被看作是微地震事件發生的潛在位置;
c、如圖2所示,根據測井信息(圖2綠線所示)獲得各個地層的速度模型,初始速度向量v=[2200,2750,3400,4800](單位m/s),初始層界面向量模型h=[424,729,1230](單位:m),其中1~4層的深度範圍依次為0m~424m,424m~779m,779m~1230m,1230m~1600m,與此對應的各層速度最大邊界值為vmax=[2500,3200,4000,5500](單位m/s),各層速度最小邊界值為vmin=[1800,2400,3000,4500](單位m/s);並讀取17道檢波器模擬資料。
d、採用振幅疊加對射孔定位並獲得能量聚焦值最大的網格中心點坐標及相應能量聚焦值e=12.7;震幅疊加方法具體如下:
d1、計算各道檢波器獲取的地震波相對於參考道的走時差δti;參考道選擇有相對清晰的初至同相軸及較高的信噪比;
式(1)表示第i道與參考道走時之差;式(1)中δlij為第i道與參考道在第j層的路徑差,vj第j層的波速;
d2、各道檢波器獲取的地震波波形根據δti逆時偏移後進行震幅疊加,表達式為:
式(2)中,各道波形在第j時刻的振幅值為a(f(t),k);m為檢波器個數,n為時窗長度;k為第j時刻的第k個採樣點;
將式(1)帶入式(2)得到:
e、將第一道檢波器(200,0)作為參考道,根據測井信息建立的初始速度模型,利用射線追蹤技術計算模擬射孔點到各參考道的理論時差δtcal,根據理論時差對各道進行偏移疊加,獲取目標函數e(v)。
δtcal=[t1-tm,t2-tm,...,tn-tm](4)
根據該理論走時差對各道檢波器獲得的射孔記錄波形進行逆時偏移疊加,目標函數(疊加能量)的數學表達式如下:
其中a為第i個體元在第j時刻的震幅大小,第i個體元的中心點坐標為(xi,yi,zi),m為檢波器個數,n為時窗長度;
f、採用極快速模擬退火算法對各層界面位置及各層速度值進行調整,首先按照上述模擬退火步驟e中第三步求取模擬退火算法初始溫度t0,
計算模擬退火初始溫度t0,獲取初始溫度的解決方法如下:
先給初始溫度一個很小的正值,然後不斷乘以一個恆大於1的數,直到滿足對任何模型的接受概率接近於1為止;
其中,v0為初始速度模型,v1為第一次迭代模型結果。得到初始溫度的近似值為100℃。
然後進行模擬退火降溫計算,所採用的極快速模擬退火降溫公式如下:
tk=t0exp(-ck1/2n)(7)
其中k為迭代次數,t0為初始退火溫度,c為給定常數用來調整算法退火溫度,這裡c=0.5;n為需要調整速度的層數;
在進行模擬退火計算過程中,還需調整速度模型向量v和層位模型向量h,具體公式為:
其中,與為各層速度的最大最小邊界值,其中與為各層位最大最小邊界值。其中sgn為符號函數,x為隨機變量,取值範圍在[-1,1]之間。μ∈[0,1];產生x表達式為:
每次迭代計算模擬退火接受概率計算如下:當e(v′)≥e(v)時,v′替代v作為當前最優解,當e(v′)<e(v)時,以概率
替代當前最優解,其中tk為第k次迭代時的溫度值。最後以e(v)>e作為本次模擬退火運算疊代終止條件。
g、將經過調整後的速度模型對射孔事件進行重定位,若定位結果滿足定位精度(誤差在5m以內)要求,即與真實射孔位置相差甚微,;若定位結果不滿足定位精度要求,即與真實射孔位置相差較大,則需對進行回火處理繼續調整速度模型,直至滿足射孔精度要求後結束。
如圖7所示,利用常規振幅疊加速度模型構建算法得到的射孔重定位結果誤差為23m,而採用本文改進後的算法重定位誤差小於2m,可見本文改進後的算法比常規算法更優。
為驗證該方法對震源定位可信度的提高,本專利在射孔周圍設置了24個震源(圖5所示),分別採用初始速度模型,原震幅疊加微地震速度模型校正算法,以及改進後速度模型校正方法構建速度模型,並對24個震源進行重定位處理,定位分布結果如圖5所示,震源定位分布誤差如圖6所示。從以上結果可以看出,採用本專利方法進行速度模型校正後,能夠有效提高射孔周邊微地震定位可信度。
