一種二維隨機載荷作用下疲勞壽命的計算方法與流程

2023-06-01 13:21:47 1

本發明涉及載荷譜分析技術，具體涉及一種二維隨機載荷(考慮載荷幅值和載荷均值均為隨機變量)作用下疲勞壽命的計算方法。
背景技術：
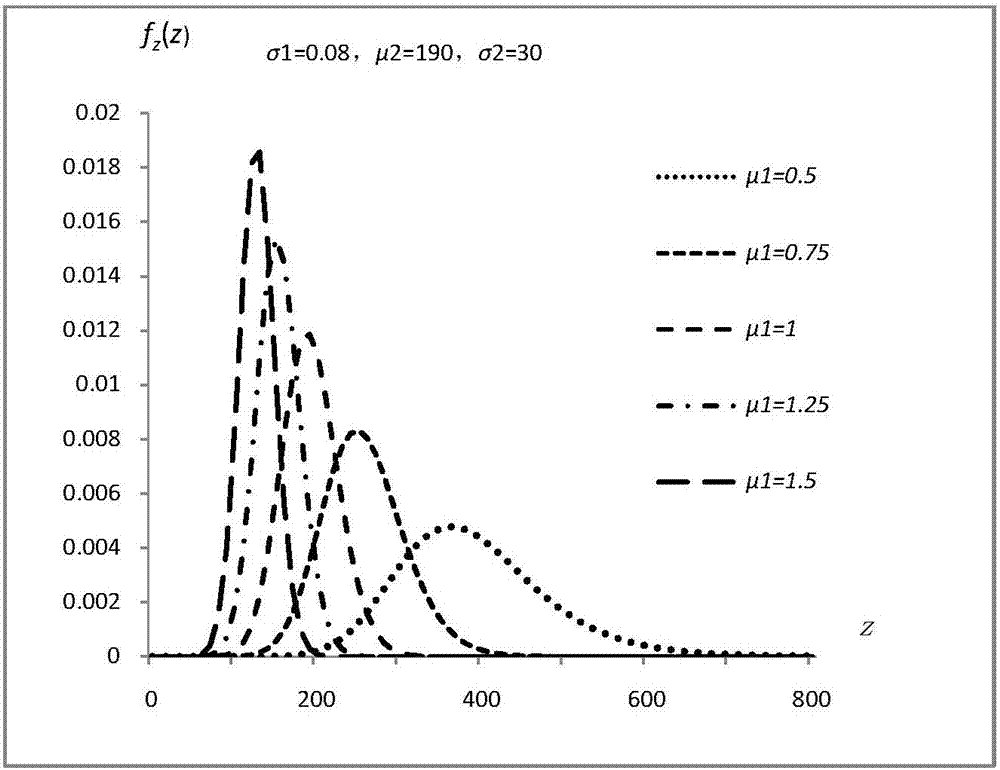
：載荷譜分析是汽車壽命預測和疲勞耐久設計過程中的一項關鍵內容。在進行疲勞耐久研究時，載荷的施加一般有兩種處理方法，一是施加循環載荷，二是施加隨機載荷。採用隨機載荷加載由於考慮了載荷的統計特性，因此要比採用循環載荷加載更符合汽車的實際使用條件。隨機載荷一般服從某種連續性的概率分布，例如正態分布、指數分布、對數正態分布、極值分布以及三參數威布爾分布等。隨機載荷作用下構件的疲勞分析應該綜合運用概率統計理論和力學分析方法來解決疲勞分析和設計中的問題。汽車在隨機載荷作用下工作時，其載荷的均值與幅值都是隨機變化的，均值與幅值在載荷譜中應視為二元隨機變量。在大多數情況下，載荷幅值x服從威布爾分布，均值y服從正態分布。由於載荷幅值和載荷均值的變化同樣都會對零件的疲勞壽命造成較大影響，為了使研究結果更符合零件的實際工作狀態，從而更準確地對零件的疲勞壽命進行預測，對基於載荷幅值和均值均為隨機變量的二維隨機載荷作用下的疲勞壽命進行深入研究是非常有必要的。二維隨機載荷作用下疲勞壽命的計算，已經成為一項亟待解決的關鍵的技術問題。技術實現要素：本發明要解決的技術問題：針對現有技術的上述問題，提供一種解決了需同時考慮載荷幅值和載荷均值各自的統計特性下的疲勞壽命的計算問題，能夠在零件設計的前期快速地、更準確地對疲勞壽命進行預測，為零件的耐久性設計提供前期參考，降低零部件在開發過程中的失效風險，從而縮短零部件的開發周期的二維隨機載荷作用下疲勞壽命的計算方法。為了解決上述技術問題，本發明採用的技術方案為：一種二維隨機載荷作用下疲勞壽命的計算方法，實施步驟包括：1)通過對目標材料進行試驗採集載荷譜數據，經統計學分析得到所述載荷譜數據的幅值、均值兩者各自的分布特性及概率密度函數；2)推算出所述載荷譜數據的當量載荷seq的概率密度函數f(seq)；3)利用式(1)所示隨機載荷作用下的miner定則和式(2)所示在整個中、長壽命區間疲勞壽命和載荷之間的三參數經驗公式得出二維隨機載荷作用下的累積疲勞損傷計算模型；nf(s-s0)β＝α(2)式(1)和式(2)中，d表示目標材料的累積疲勞損傷，n表示目標材料受到的循環載荷總數量，f(s)表示隨機載荷的概率密度函數，nf表示目標材料在載荷s作用下的疲勞壽命，s表示目標材料受到的載荷，s0表示為常數的載荷係數，α、β為常數係數；4)根據所述累積疲勞損傷計算模型反求累積疲勞損傷等於1時的疲勞壽命計算模型；5)根據所述疲勞壽命計算模型求得目標材料在二維隨機載荷作用下的疲勞壽命。優選地，步驟2)的詳細步驟包括：2.1)根據goodman公式中式(3)所示當量載荷seq的表達式中載荷幅值sa的概率密度函數求得y＝sa的概率密度函數fy(y)，並根據載荷均值sm的概率密度函數求出材料的拉伸強度σb和載荷均值sm的差值除以拉伸強度σb之商x的概率密度函數fx(x)；式(3)中，σb表示目標材料的拉伸強度，sa表示載荷幅值，sm表示載荷均值；2.2)根據式(4)求解得到當量載荷seq的概率密度函數f(seq)；式(4)中，fz(y/x)表示當量載荷seq的概率密度函數，變量z等於y除以x，y表示目標材料的載荷幅值sa，x表示目標材料的拉伸強度σb和載荷均值sm的差值除以拉伸強度σb之商。優選地，步驟2.2)求解得到當量載荷seq的概率密度函數f(seq)如式(5)所示；式(5)中，f(seq)表示當量載荷seq的概率密度函數，目標材料的載荷為載荷幅值sa和載荷均值sm都符合正態分布，且載荷幅值sa和載荷均值sm相互獨立的二維隨機載荷，其中載荷幅值sa服從n(μa,σa2)，載荷均值sm服從n(μm,σm2)，μa表示載荷幅值sa的均值，σa2表示載荷幅值sa的方差，μm表示載荷均值sm的均值，σm2表示載荷均值sm的方差，a、b、c、σ1、σ2、μ1、μ2均為中間參數，中間參數μ2的取值與載荷幅值sa的均值μa相同，σ22的取值與載荷幅值sa的方差σa2相同，中間參數μ1的取值為μ1＝-μm/σb+1，σb表示目標材料的拉伸強度，變量z等於y除以x，y表示目標材料的載荷幅值sa，x表示目標材料的拉伸強度σb和載荷均值sm的差值除以拉伸強度σb之商，q為積分變量。優選地，步驟3)中二維隨機載荷作用下的累積疲勞損傷計算模型如式(6)所示；式(6)中，d表示目標材料的累積疲勞損傷，n表示目標材料受到的循環載荷總數量，f(seq)表示當量載荷seq的概率密度函數，s0表示為常數的載荷係數，α、β為常數係數。優選地，步驟4)中的疲勞壽命計算模型如式(7)所示；式(7)中，nf表示疲勞壽命，α、β為常數係數，f(seq)表示當量載荷seq的概率密度函數，s0表示為常數的載荷係數。優選地，步驟5)的詳細步驟包括：將所述疲勞壽命計算模型通過gauss-legendre求積公式進行積分運算，從而計算得出目標材料在二維隨機載荷作用下的疲勞壽命。優選地，步驟5)的詳細步驟包括：根據式(8)計算疲勞壽命對應的等效載荷sd，根據等效載荷sd求得對應的疲勞壽命作為目標材料在二維隨機載荷作用下的疲勞壽命；式(8)中，sd表示疲勞壽命對應的等效載荷，s0表示為常數的載荷係數，nf表示疲勞壽命，α、β為常數係數本發明二維隨機載荷作用下疲勞壽命的計算方法具有下述優點：本發明的計算方法由於充分考慮了載荷幅值和載荷均值各自的統計特性，使得載荷的加載更符合零件的實際工作狀態，從而能更準確地對疲勞壽命進行計算。採用該方法可以在零件設計的前期快速地、更準確地對疲勞壽命進行預測，為零件的耐久性設計提供前期參考，降低零部件在開發過程中的失效風險，從而縮短零部件的開發周期。附圖說明圖1為本發明實施例一方法的基本流程示意圖。圖2為本發明實施例一中參數μ1不同分布下的概率密度函數曲線對比圖。圖3為本發明實施例一中參數σ1不同分布下的概率密度函數曲線對比圖。圖4為本發明實施例一中參數μ2不同分布下的概率密度函數曲線對比圖。圖5為本發明實施例一中參數σ2不同分布下的概率密度函數曲線對比圖。具體實施方式實施例一：如圖1所示，本實施例二維隨機載荷作用下疲勞壽命的計算方法的實施步驟包括：1)通過對目標材料進行試驗採集載荷譜數據，經統計學分析得到所述載荷譜數據的幅值、均值兩者各自的分布特性及概率密度函數；2)推算出所述載荷譜數據的當量載荷seq的概率密度函數f(seq)；3)利用式(1)所示隨機載荷作用下的miner定則和式(2)所示在整個中、長壽命區間疲勞壽命和載荷之間的三參數經驗公式得出二維隨機載荷作用下的累積疲勞損傷計算模型；nf(s-s0)β＝α(2)式(1)和式(2)中，d表示目標材料的累積疲勞損傷，n表示目標材料受到的循環載荷總數量，f(s)表示隨機載荷的概率密度函數，nf表示目標材料在載荷s作用下的疲勞壽命，s表示目標材料受到的載荷，s0表示為常數的載荷係數，α、β為常數係數；4)根據所述累積疲勞損傷計算模型反求累積疲勞損傷等於1時的疲勞壽命計算模型；5)根據所述疲勞壽命計算模型求得目標材料在二維隨機載荷作用下的疲勞壽命。本實施例中，步驟2)的詳細步驟包括：2.1)根據goodman公式中式(3)所示當量載荷seq的表達式中載荷幅值sa的概率密度函數，求出y＝sa的概率密度函數fy(y)，並根據載荷均值sm的概率密度函數求出材料的拉伸強度σb和載荷均值sm的差值除以拉伸強度σb之商x的概率密度函數fx(x)；式(3)中，σb表示目標材料的拉伸強度，sa表示載荷幅值，sm表示載荷均值；2.2)根據式(4)求解得到當量載荷seq的概率密度函數f(seq)；式(4)中，fz(y/x)表示當量載荷seq的概率密度函數，變量z等於y除以x，y表示目標材料的載荷幅值sa，x表示目標材料的拉伸強度σb和載荷均值sm的差值除以拉伸強度σb之商。為了計算二維隨機載荷作用下的疲勞壽命，本實施例提供了載荷幅值和載荷均值都符合正態分布的二維隨機載荷的當量載荷seq的概率密度函數f(seq)。本實施例中，步驟2.2)求解得到當量載荷seq的概率密度函數f(seq)如式(5)所示；式(5)中，f(seq)表示當量載荷seq的概率密度函數，目標材料的載荷為載荷幅值sa和載荷均值sm都符合正態分布，且載荷幅值sa和載荷均值sm相互獨立的二維隨機載荷，其中載荷幅值sa服從n(μa,σa2)，載荷均值sm服從n(μm,σm2)，μa表示載荷幅值sa的均值，σa2表示載荷幅值sa的方差，μm表示載荷均值sm的均值，σm2表示載荷均值sm的方差，a、b、c、σ1、σ2、μ1、μ2均為中間參數，中間參數μ2的取值與載荷幅值sa的均值μa相同，σ22的取值與載荷幅值sa的方差σa2相同，中間參數μ1的取值為μ1＝-μm/σb+1，σb表示目標材料的拉伸強度，變量z等於y除以x，y表示目標材料的載荷幅值sa，x表示目標材料的拉伸強度σb和載荷均值sm的差值除以拉伸強度σb之商，q為積分變量。本實施例中，步驟3)中二維隨機載荷作用下的累積疲勞損傷計算模型如式(6)所示；式(6)中，d表示目標材料的累積疲勞損傷，n表示目標材料受到的循環載荷總數量，f(seq)表示當量載荷seq的概率密度函數，s0表示為常數的載荷係數，α、β為常數係數。本實施例中，步驟4)中的疲勞壽命計算模型如式(7)所示；式(7)中，nf表示疲勞壽命，α、β為常數係數，f(seq)表示當量載荷seq的概率密度函數，s0表示為常數的載荷係數。本實施例中，步驟5)的詳細步驟包括：將所述疲勞壽命計算模型通過gauss-legendre求積公式進行積分運算，從而計算得出目標材料在二維隨機載荷作用下的疲勞壽命。本實施例中，分別針對中間參數σ1、σ2、μ1、μ2進行不同取值，並分別將不同中間參數取值情況下的當量載荷seq的概率密度函數f(seq)(圖中表達為fz(z))生成曲線，分別得到圖2、圖3、圖4、圖5。圖2記載了σ1取值0.08、σ2取值30、μ2取值190的情況下，μ1分別取值為0.5、0.75、1、1.25、1.5時概率密度函數f(seq)的對比曲線。圖3記載了σ2取值30、μ1取值0.75、μ2取值190的情況下，σ1分別取值為0.05、0.06、0.07、0.08、0.09、0.1時概率密度函數f(seq)的對比曲線。圖4記載了σ1取值0.08，σ2取值30，μ1取值0.75的情況下，μ2分別取值為150、170、190、210、230、250時概率密度函數f(seq)的對比曲線。圖5記載了σ1取值0.08，μ1取值0.75、μ2取值190的情況下，σ2分別取值為5、10、20、30、40、50時概率密度函數f(seq)的對比曲線。對圖2～圖5進行分析可以得出：1)fz(z)函數的圖形形狀和正態分布函數形狀相似，主要為以下三點：a)函數值具有峰值點，且z離峰值點越遠，函數值越小；b)函數在峰值點兩側都有拐點；c)曲線以水平軸為漸近線。2)在其它三個參數不變的情況下，μ1的減小、σ1、μ2、σ2的增加使函數峰值減小，同時函數曲線形狀變平緩。3)μ2的增加使峰值點向右移動，μ1和σ1的增加使峰值點向左移動，σ2的變化不改變峰值點位置。實施例二：本實施例中與實施例一基本相同，其主要區別點為：步驟5)根據所述疲勞壽命計算模型求得目標材料在二維隨機載荷作用下的疲勞壽命的方法不同。本實施例中，將對疲勞壽命的研究轉化為等效載荷的研究。定義等效載荷如下：從總的作用效果來看，在隨機載荷與循環載荷兩類載荷作用下的最終結果都將導致構件的損傷狀態達到臨界值而發生失效,可以認為對應於某隨機載荷過程，一定存在一個與它等效的恆幅載荷，使得構件在相同的初始狀態下，經過相同的作用時間同時發生損壞。定義該恆幅載荷為隨機載荷的等效載荷，用sd表示。等效載荷和疲勞壽命的對應關係式見三參數經驗公式。本實施例中，步驟5)的詳細步驟包括：根據式(8)計算疲勞壽命對應的等效載荷sd，根據等效載荷sd求得對應的疲勞壽命作為目標材料在二維隨機載荷作用下的疲勞壽命；式(8)中，sd表示疲勞壽命對應的等效載荷，s0表示用等效應力幅表示的理論疲勞極限，nf表示疲勞壽命，α、β為常數係數。以16mn材料為例，根據現有研究，α＝3.95×108，s0＝261mpa，β＝2。根據式(7)和式(8)，16mn材料在二維隨機載荷作用下的等效載荷為：式(10)中，sd表示疲勞壽命對應的等效載荷，seq表示當量載荷。針對不同載荷幅值和載荷均值的統計分布參數下，仍採用gauss-legendre求積公式對函數進行積分運算，計算得出部分等效載荷數據見表1～表5，同時為了進行比較，計算一維隨機載荷的等效載荷見表6。在得出等效載荷以後，根據式(8)反推即可得出疲勞壽命。表1：不同μ1、σ1的等效載荷(mpa)(μ2＝210，σ2＝40)。μ1\σ10.050.060.070.080.090.10.5>600>600>600>600>600>6000.75314316344417526>60012702712722732742751.252622622622622632631.5261261261261261261表2：不同μ2、σ2的等效載荷(mpa)(μ1＝0.75，σ1＝0.05)。σ2\μ21501701902102302501026226527429131434020264270281298319343302692772893063253484027628529831433335450283294307323341362表3：不同μ2、σ2的等效載荷(mpa)(μ1＝1，σ1＝0.05)。σ2\μ21501701902102302501026126126126126326820261261261263266273302612622632662712794026226426627027728650264267271276283292表4：不同μ2、σ2的等效載荷(mpa)(μ1＝1，σ1＝0.1)。表5：不同μ2、σ2的等效載荷(mpa)(μ1＝1.25，σ1＝0.1)。σ2\μ21501701902102302501026126126126126126220261261261261262263302612612612622632644026126126226326426750262262263265267270表6：一維隨機載荷的等效載荷(mpa)。σ\μ1501701902102302501026126126126126126420261261261262264270302612612622652692774026226326526927528450264266269274281291根據分析結果，載荷均值對二維正態隨機載荷的等效載荷有較大的影響，在載荷均值sm的均值μm小於0時，等效載荷迅速減小甚至低於一維隨機載荷的等效載荷；當μm等於0時，考慮載荷均值的等效載荷比不考慮載荷均值的等效載荷略高；當μm大於0時，隨著μ2、σ2的增加，二維隨機載荷的等效載荷迅速增加，直至遠大於一維隨機載荷的等效載荷。以上所述僅是本發明的優選實施方式，本發明的保護範圍並不僅局限於上述實施例，凡屬於本發明思路下的技術方案均屬於本發明的保護範圍。應當指出，對於本
技術領域：
的普通技術人員來說，在不脫離本發明原理前提下的若干改進和潤飾，這些改進和潤飾也應視為本發明的保護範圍。當前第1頁12