一種基於灰色ELM神經網絡的短時交通流量預測的方法與流程
2023-07-25 08:06:01 1
本發明涉及短時交通流量預測的技術領域,特別是指一種基於灰色elm神經網絡的短時交通流量預測的方法。
背景技術:
隨著經濟的發展,對汽車需求的不斷增加,公路交通流量也隨之增加,由此帶來了一系列的交通問題。在不改變當前路網的情況下,通過智能交通控制系統實現對路網的疏導和控制,是解決交通問題的有效途徑。準確的交通流預測是交通流的疏導和控制的基礎,是智能交通管理系統的重要組成部分。
交通流本身具有很強的不確定性,是複雜、多變的,容易受到隨機的擾動,並且規律性不明顯,隨著不同的預測方法的引入,對短時交通流的預測也出現了許多預測模型,但是現有的預測方法對數據波動性要求較高和易失真的特點。
技術實現要素:
本發明為解決現有的問題,提出一種基於灰色elm神經網絡的短時交通流量預測的方法。
本發明的技術方案是這樣實現的:
一種基於灰色elm神經網絡的短時交通流量預測的方法,其步驟包括:
a.對數據進行灰色處理,將採集到的數據按照式(3)進行分組,即:設採集到的數據為q,則
q=(q1,q2,…,qm),(m∈n+)(1)
將其分為n組,每組m+1個數據,且滿足
n+m=m,(n∈n+,m∈n+)(2)
對於其中的第p(p=1,2,…,n)組,記為:
經過式(3)得到等維新息序列後,按照式(4)和(5)進行累加,得到累加後的等維新息序列,即:對中的數據進行灰色處理,得到一次累加序列為
其中
b.生成輸入矩陣集和目標輸出矩陣集,對累加後的等維新息序列按照式(6)、式(7)、式(8)處理,得到網絡的輸入矩陣和目標輸出矩陣,即:選取的前m項作為elm神經網絡的輸入,第m+1項作為網絡的期望輸出,則有
對以上分成n組數據,由其構成的網絡的輸入矩陣集x和目標輸出矩陣集y分別為
x=[x1,x2,…,xn](7)
y=[y1,y2,…,yn](8)
設網絡的實際輸出矩陣t為
t=[t1,t2,…,tn](9);
c.建立elm神經網絡模型,先隨機生成網絡的權值和閾值,設定好網絡參數,網絡參數設置如下:
wij,(i=1,2,…,l,j=1,2,…,m)為輸入層和隱含層之間的連接權值,其中l∈n+,為隱層神經元個數,並記wi=(wi1,wi2,…,wim);
bi,(i=1,2,…,l)為隱含層第i個的節點的閾值;
β為隱含層和輸出層的權值,其中βi,(i=1,2,…,l)為隱含層第i個節點與輸出層節點的連接權值;
d.網絡訓練,將步驟b中生成的輸入矩陣集合目標輸出矩陣集輸入神經網絡,對網絡進行訓練,網絡訓練原理為:
隱層激勵函數為sigmoid函數,表達式為:
當輸入為xp時,根據神經網絡原理有:
隱層第i個節點的輸入為
neti=wixp+bi(11)
隱層第i個節點的輸出為
si=f(neti)=f(wixp+bi)(12)
網絡的輸出層的輸出為
當輸入為x時,記隱含層的輸出矩陣為h,有
對於輸出層,則有輸出方程為:
t=hβ(15)
網絡訓練的目的就是找到最優輸出層權值使網絡的實際輸出t無限逼近於目標輸出y,通過求取最小範數二乘解的方法得到最優輸出層權值即:
其中,h+為moore-penrose逆,
e.仿真測試,利用求解到的最優權值求得最優輸出層權值下的elm神經網絡的預測輸出為:
f.將預測結果累減還原成實際預測結果,用網絡預測結果減去步驟b得到的等維新息序列的累加值,得到實際預測結果,通過累減得到實際預測值為:
本測量方法首先對原始數據進行分組,構建等維新息序列,對等維新息序列進行灰色處理,得到灰色處理後的等維新息序列;然後對等維新息序列進行處理,構成輸入矩陣集和目標輸出矩陣集,對elm神經網絡進行訓練,從而得到elm神經網絡對灰色數據的預測結果;最後通過累減還原,得到短時交通流的真實預測結果。
本發明的有益效果是:elm神經網絡有著訓練簡單,訓練速度快的特點,對交通流數據採用灰色模型累加處理,降低了交通流數據隨機性,更有效減小因數據本身波動造成的誤差。經仿真驗證,相比於現有的一些預測方法,該方法提高了預測精度,是一種有效的短時交通流預測方法。
附圖說明
為了更清楚地說明本發明實施例或現有技術中的技術方案,下面將對實施例或現有技術描述中所需要使用的附圖作簡單地介紹,顯而易見地,下面描述中的附圖僅僅是本發明的一些實施例,對於本領域普通技術人員來講,在不付出創造性勞動的前提下,還可以根據這些附圖獲得其他的附圖。
圖1為elm神經網絡的架構圖;
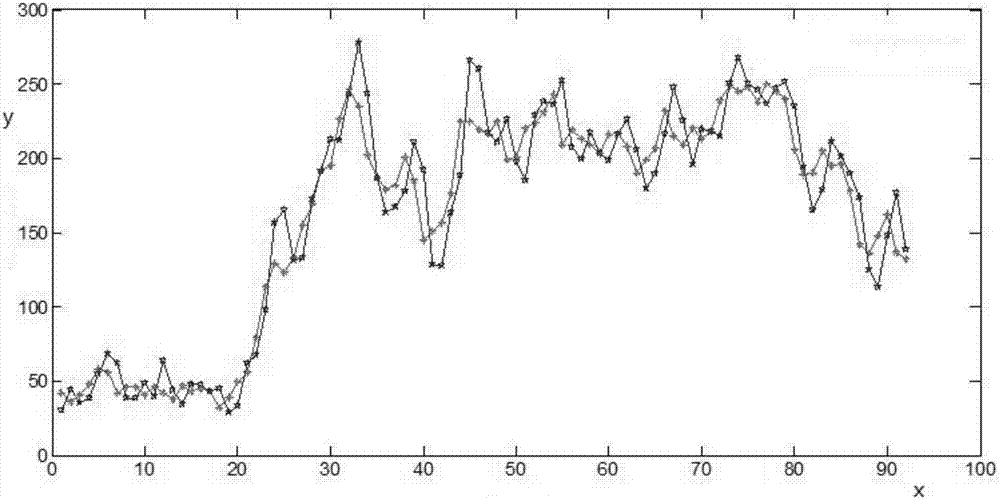
圖2為灰色模型預測結果與實際值的對比圖;
圖3為elm神經網絡預測結果與實際值的對比圖;
圖4為利用灰色模型和bp網絡組合模型的預測結果與實際值的對比圖;
圖5為帶有慣性因子的組合模型的預測結果與實際值的對比圖;
圖6為貝葉斯組合模型的預測結果與實際值的對比圖;
圖7為灰色elm網絡的預測結果與實際值的對比圖;
圖8為六種預測模型的預測結果綜合對比圖。
其中x軸為時間點,y軸為交通流量;藍色曲線為預測交通流量,紅色曲線為實際交通流量。
具體實施方式
下面將結合本發明實施例中的附圖,對本發明實施例中的技術方案進行清楚、完整地描述,顯然,所描述的實施例僅僅是本發明一部分實施例,而不是全部的實施例。基於本發明中的實施例,本領域普通技術人員在沒有付出創造性勞動前提下所獲得的所有其他實施例,都屬於本發明保護的範圍。
一種基於灰色elm神經網絡的短時交通流量預測的方法,其步驟包括:
a.對數據進行灰色處理,將採集到的數據按照式(3)進行分組,即:設採集到的數據為q,則
q=(q1,q2,…,qm),(m∈n+)(1)
將其分為n組,每組m+1個數據,且滿足
n+m=m,(n∈n+,m∈n+)(2)
對於其中的第p(p=1,2,…,n)組,記為:
經過式(3)得到等維新息序列後,按照式(4)和(5)進行累加,得到累加後的等維新息序列,即:對中的數據進行灰色處理,得到一次累加序列為
其中
b.生成輸入矩陣集和目標輸出矩陣集,對累加後的等維新息序列按照式(6)、式(7)、式(8)處理,得到網絡的輸入矩陣和目標輸出矩陣,即:選取的前m項作為elm神經網絡的輸入,第m+1項作為網絡的期望輸出,則有
對以上分成n組數據,由其構成的網絡的輸入矩陣集x和目標輸出矩陣集y分別為
x=[x1,x2,…,xn](7)
y=[y1,y2,…,yn](8)
設網絡的實際輸出矩陣t為
t=[t1,t2,…,tn](9);
c.建立elm神經網絡模型,先隨機生成網絡的權值和閾值,設定好網絡參數,網絡參數設置如下:
wij,(i=1,2,…,l,j=1,2,…,m)為輸入層和隱含層之間的連接權值,其中l∈n+,為隱層神經元個數,並記wi=(wi1,wi2,…,wim);
bi,(i=1,2,…,l)為隱含層第i個的節點的閾值;
β為隱含層和輸出層的權值,其中βi,(i=1,2,…,l)為隱含層第i個節點與輸出層節點的連接權值;
d.網絡訓練,將步驟b中生成的輸入矩陣集合目標輸出矩陣集輸入神經網絡,對網絡進行訓練,網絡訓練原理為:
隱層激勵函數為sigmoid函數,表達式為:
當輸入為xp時,根據神經網絡原理有:
隱層第i個節點的輸入為
neti=wixp+bi(11)
隱層第i個節點的輸出為
si=f(neti)=f(wixp+bi)(12)
網絡的輸出層的輸出為
當輸入為x時,記隱含層的輸出矩陣為h,有
對於輸出層,則有輸出方程為:
t=hβ(15)
網絡訓練的目的就是找到最優輸出層權值使網絡的實際輸出t無限逼近於目標輸出y,通過求取最小範數二乘解的方法得到最優輸出層權值即:
其中,h+為moore-penrose逆,
e.仿真測試,利用求解到的最優權值求得最優輸出層權值下的elm神經網絡的預測輸出為:
f.將預測結果累減還原成實際預測結果,用網絡預測結果減去步驟b得到的等維新息序列的累加值,得到實際預測結果,通過累減得到實際預測值為:
本測量方法首先對原始數據進行分組,構建等維新息序列,對等維新息序列進行灰色處理,得到灰色處理後的等維新息序列;然後對等維新息序列進行處理,構成輸入矩陣集和目標輸出矩陣集,對elm神經網絡進行訓練,從而得到elm神經網絡對灰色數據的預測結果;最後通過累減還原,得到短時交通流的真實預測結果。
具體應用舉例:採用焦作市普濟路與人民路交叉口東西方向單向交通流量為研究對象,採集每天4點到12點的每5分鐘的交通流量共96個數據,連續採集4天。前三天的數據用於網絡訓練,第四天的流量數據用於測試灰色elm網絡模型。
選取m=4,則網絡的輸入和輸出神經元個數分別是4和1,根據elm神經網絡原理,選取隱層神經元個數為單天採集的流量生成的等維新息序列的個數,為92個,則網絡的模型為4-92-1;訓練前,先給定權值w,並給定閾值為b=1,隱層激勵函數選用sigmoid函數,計算輸出矩陣,訓練網絡,然後用訓練好的網絡進行預測。
通過圖2可以看出,灰色模型在進行短時交通預測時,誤差較大,且當數據本身不平穩時,預測結果往往很差,elm神經網絡通過對歷史數據的訓練,預測精度有了進一步提高;灰色elm神經網絡在elm神經網絡的基礎上,通過對數據的累加,使得測試數據與訓練數據的差異性更小,有效提高了預測精度;與其它組合模型相比,預測精度也有所提高。
通過圖8對六種預測模型的對比可以看出,灰色elm神經網絡預測模型在預測精度上要遠優於灰色模型和elm神經網絡預測模型,也優於現有的一些組合模型,在最大誤差,平均絕對誤差,平均相對誤差方面都有所減小。
以上所述僅為本發明的較佳實施例而已,並不用以限制本發明,凡在本發明的精神和原則之內,所作的任何修改、等同替換、改進等,均應包含在本發明的保護範圍之內。
