一種圖像重構方法及系統與流程
2023-05-19 10:47:46 2
本申請涉及圖像重構技術領域,特別涉及一種圖像重構方法及系統。
背景技術:
作為光學顯微鏡的一種,螢光顯微鏡是現代生命科學研究中必不可少的研究工具,然而傳統光學顯微鏡的解析度受到衍射極限的限制。近年來,一系列突破衍射極限的超分辨顯微成像技術相繼出現,例如隨機光學重構顯微鏡、光激活定位顯微鏡、螢光光激活定位顯微鏡、受激發射損耗顯微鏡、結構光照明顯微鏡等。結構光照明顯微鏡(structuredilluminationmicroscope,sim)是目前主流的超分辨成像技術之一。該技術採用加載了一定頻率信息的結構光對樣品進行照明(以下統稱為照明光),將傳統顯微鏡無法獲取的高頻信息編碼到採集圖像中,再通過圖像處理算法對樣品信息進行重構,其橫向解析度可以達到傳統解析度的兩倍。
超分辨重構算法是sim的核心技術之一,其算法主要步驟包括:圖像預處理、頻譜分離、計算照明光空間頻率、參數修正、去卷積、頻譜平移以及頻譜融合。影響重構圖像質量的因素有很多,例如:平移相位不準確而導致的頻譜分離不徹底、照明光參數的求解誤差、去卷積過程引入的噪聲放大、點擴散函數誤差、離焦光線等。實驗系統中照明光參數主要有空間頻率、方向、調製度和初始相位等參數,由於實驗系統的不穩定,這些參數是無法預先知道的,只能通過一系列原始測量數據對這些參數進行求解,其求解精度對最終重構圖像的質量有重要影響。
目前,照明光參數的求解算法主要有以下幾種方法:文獻1[phase-shiftestimationinsinusoidallyilluminatedimagesforlateralsuperresolution]通過分析原始數據在頻域中的峰值點的位置及其相位來確定照明光的空間頻率和相位,這種方法對於高頻率的照明光和信噪較大的數據並不適用;文獻2[surpassingthelateralresolutionlimitbyafactoroftwousingstructuredilluminationmicroscopy]通過計算平移之後與之前的組分進行互相關,進而求解得到照明光參數,但此方法計算量大,耗時較長,不適用於sim數據的快速處理;文獻3[phaseoptimisationforsturcturedilluminationmicroscopy]在文獻2的基礎上增加了迭代優化算法,加快了算法的計算效率,但算法較為複雜,計算精度與初始值有關,初始值不當會引起算法無法收斂至準確值。
技術實現要素:
本申請提供了一種圖像重構方法及系統,旨在至少在一定程度上解決現有技術中的上述技術問題之一。
為了解決上述問題,本申請提供了如下技術方案:
一種圖像重構方法,包括:
步驟a:對圖像進行頻譜分離,得到所述圖像的頻譜分量;
步驟b:對所述頻譜分量進行峰值點搜索,獲取照明光的方向和空間頻率;
步驟c:通過線性擬合算法計算所述照明光的調製度和初始相位,通過所述照明光的調製度和初始相位對所述頻譜分量進行修正,將所述頻譜分量的係數進行歸一化;
步驟d:對所述歸一化的頻譜分量進行去卷積和平移處理,並將所述去卷積和平移處理後的頻譜分量進行頻譜組合,得到所述圖像的重構結果。
本申請實施例採取的技術方案還包括:所述步驟a還包括:對所述圖像進行預處理;所述預處理包括:對所述圖像進行光強修正,並對所述圖像的邊緣進行模糊化處理。
本申請實施例採取的技術方案還包括:在所述步驟b中,所述獲取照明光的方向和空間頻率具體包括:根據照明光的空間頻率初始值設定濾波函數,對所述頻譜分量進行濾波,對所述濾波後的頻譜分量進行峰值點搜索,確定濾波後的頻譜分量的最大值,並在所述最大值附近±1個像素的範圍內,採用質心法確定所述峰值點位置,並精確到亞像素,進而得到所述照明光的方向和空間頻率。
本申請實施例採取的技術方案還包括:在所述步驟c中,所述通過照明光的調製度和初始相位對頻譜分量進行修正具體包括:
步驟c1:中心組分的匹配:中心組分的表達式為:
上述公式中,是光學傳遞函數,d=1,2,3;n=0,1,2;m=-1,0,1,是頻譜分量,假設b=s*a,則s=c1,0/cd,0,通過對表達式a和b進行線性擬合得到參數s,並將所有其他組分用參數s進行修正,即:
其中表示將d1用d2替換;
步驟c2:邊緣組分與中心組分進行匹配:根據傅立葉頻移定理:
首先將邊緣頻譜變換到實域,乘以相移因子再變換至頻域,得到移位之後的頻譜:
同理,獲得平移之後的otf,即得到表達式a和b:
假設b=s*a,通過複數線性擬合得到參數邊緣組分修正為:
本申請實施例採取的技術方案還包括:在所述步驟c中,所述通過線性擬合算法計算照明光的調製度和初始相位具體為:考慮到噪聲和計算誤差的存在,需要對表達式a和b內的數據進行篩選。首先計算表達式a和b的有效支持域,對於中心組分修正,所述支持域取|otf|>0.1的區域,對於邊緣組分修正,所述有效支持域為和的重疊區域;然後由有效支持域內a和b的數據組成數據對(ai,bi),並對數據對(ai,bi)進行進一步篩選,由於噪聲的存在,|bi|與|ai|的比值分布範圍較大,但大部分數值集中在一定區域內,所以選擇比值|bi|/|ai|分布在其最大概率附近的數據組作為有效數據。最後對所述有效數據對進行複數線性擬合,得到參數s的估計,即
本申請實施例採取的另一技術方案為:一種圖像重構系統,包括:
頻譜分離模塊:用於對圖像進行頻譜分離,得到所述圖像的頻譜分量;
照明光參數計算模塊:用於對所述頻譜分量進行峰值點搜索,獲取照明光的方向和空間頻率;
參數修正模塊:用於通過線性擬合算法計算所述照明光的調製度和初始相位,通過所述照明光的調製度和初始相位對所述頻譜分量進行修正,將所述頻譜分量的係數進行歸一化;
頻譜平移模塊:用於對所述歸一化的頻譜分量進行去卷積和平移處理;
頻譜組合模塊:用於將所述去卷積和平移處理後的頻譜分量進行頻譜組合,得到所述圖像的重構結果。
本申請實施例採取的技術方案還包括圖像預處理模塊,所述圖像預處理模塊用於對圖像進行預處理;所述預處理包括:對所述圖像進行光強修正,並對所述圖像的邊緣進行模糊化處理。
本申請實施例採取的技術方案還包括:所述照明光參數計算模塊獲取照明光的方向和空間頻率具體為:根據照明光的空間頻率初始值設定濾波函數,對所述頻譜分量進行濾波,對所述濾波後的頻譜分量進行峰值點搜索,確定濾波後的頻譜分量的最大值,並在所述最大值附近±1個像素的範圍內,採用質心法確定所述峰值點位置,得到所述照明光的方向和空間頻率。
本申請實施例採取的技術方案還包括:所述參數修正模塊通過照明光的調製度和初始相位對頻譜分量進行修正具體包括:
中心組分的匹配:中心組分的表達式為:
式中,是光學傳遞函數,d=1,2,3;n=0,1,2;m=-1,0,1,是頻譜分量,假設b=s*a,則s=c1,0/cd,0,通過對表達式a和b進行線性擬合得到參數s,並將所有其他組分用參數s進行修正,即:其中表示將d1用d2替換;
邊緣組分與中心組分進行匹配:
將邊緣頻譜變換到實域,乘以相移因子再變換至頻域,得到移位之後的頻譜:
獲得平移之後的otf,即得到表達式a和b:
假設b=s*a,通過複數線性擬合得到參數邊緣組分修正為:
本申請實施例採取的技術方案還包括:所述參數修正模塊通過線性擬合算法計算照明光的調製度和初始相位具體為:計算表達式a和b的有效支持域,取|otf|>0.1的區域,所述有效支持域為和的重疊區域;由有效支持域內a和b的數據組成數據對(ai,bi),並對數據對(ai,bi)進行數據篩選,得到有效數據對,所述有效數據對通過複數線性擬合進行參數s的估計,即
相對於現有技術,本申請實施例產生的有益效果在於:本申請實施例的圖像重構方法及系統利用理想相位對預處理圖像進行頻譜分離,根據照明光空間頻率初始值設定濾波函數,對分離頻譜進行濾波,再進行峰值點搜索,並通過質心法將峰值點的定位精度提高至亞像素級,以確定照明光的空間頻率。該方法儘可能地排除了其他幹擾信息,在此基礎上進行峰值點查找,可以提高空間頻率的求解精度。採用簡單而有效的線性擬合算法求解照明光的調製度和初始相位,並在此基礎上增加數據篩選功能,避免了繁瑣而耗時的互相關算法,同時又提高了求解精度;並利用計算得到的調製度和初始相位對頻譜分量進行參數歸一化,從而有效提高重構圖像的質量。
附圖說明
圖1是本申請實施例的圖像重構方法的流程圖;
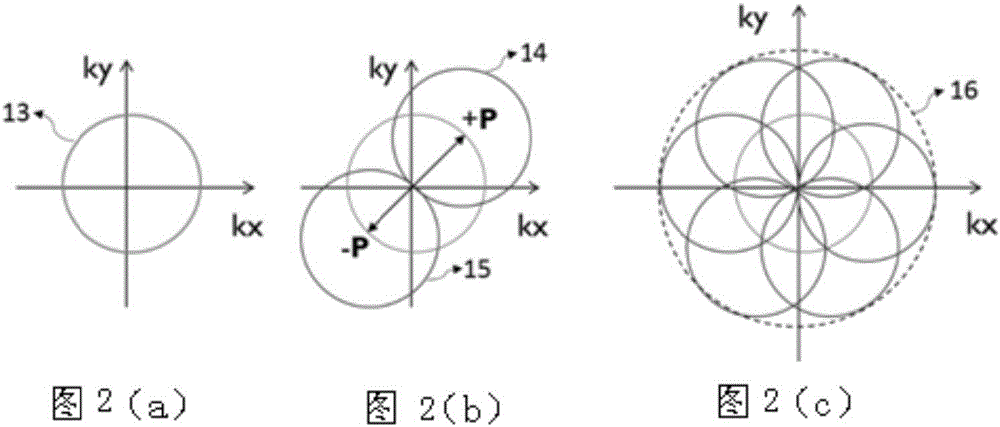
圖2為sim超分辨原理圖;
圖3為本申請實施例的頻譜分量濾波示意圖;
圖4是本申請實施例的圖像重構系統的結構示意圖;
圖5為本申請實施例的圖像重構結果示意圖;其中,圖5(a)表示無參數修正部分的圖像重構結果;圖5(b)表示有參數修正部分的圖像重構結果;圖5(c)表示寬場成像結果。
具體實施方式
為了使本申請的目的、技術方案及優點更加清楚明白,以下結合附圖及實施例,對本申請進行進一步詳細說明。應當理解,此處所描述的具體實施例僅用以解釋本申請,並不用於限定本申請。
請參閱圖1,是本申請實施例的圖像重構方法的流程圖。本申請實施例的圖像重構方法包括以下步驟:
步驟10:對sim成像系統採集到的原始圖像進行預處理;
在步驟10中,sim成像系統的成像原理為:sim是一個線性移不變光學系統,圖像是樣品發射信息與系統psf(pointspreadfunction,點擴散函數)的卷積:
在公式(1)中,是被測的樣品信息,是照明光,是系統psf。在線性sim中,照明光通常為正弦條紋,可表示為:
在公式(2)中,為照明光的空間頻率矢量,表示了照明光的周期和方向,a表示照明光的調製度。結合公式(1)和(2),圖像的頻域表達式為:
在公式(3)中,m=-1,0,1,符號(~)表示時域變量的頻域表達式,是光學傳遞函數(opticaltransferfunction,otf)。可見,每幅採集得到的原始圖像都是由0和±1級頻譜分量組合而成。
為了將三個頻譜分量分離,需要改變照明光的相位,照明光的相位值為初始相位和平移相位之和,即初始相位是未知的,與照明光的絕對位置有關,平移相位一般取0~2π上等間隔分布的相位,即為了均勻的提高解析度,一般採用相隔60度的三個照明光方向,如此,sim至少需要採集9幅原始圖像。由於系統誤差,每個方向上的照明光的調製度、初始相位和空間頻率是不同的,公式(3)又可以表示為:
在公式(4)中,d表示照明光的方向,n表示平移相位,m表示頻譜分量,d=1,2,3;n=0,1,2;m=-1,0,1,是待分離的頻譜分量。
sim超分辨原理如圖2所示。圖2(a)中,13表示傳統寬場顯微鏡可觀測到的樣品頻域信息,由於系統otf的支持域有限,支持域外的高頻信息無法獲取,因此解析度受限。採用正弦結構光對樣品進行照明,如公式(4)所示,sim獲取的樣品信息中含有高頻組分,圖2(b)中,14和15則表示某方向上被平移至正確位置的高頻分量,可見,在此方向上,解析度有所提高。為了均勻提高系統解析度,照明光採用三個方向,將所有方向上的頻譜分量疊加,就得到圖2(c)中16所示的區域。相比於13,區域16所示的系統解析度最大可提高2倍。
在圖像採集過程中,由於相機曝光時間和照明光強的浮動,需要對測量序列中的所有原始圖像進行光強修正,保證每幅圖像的平均值相同。另一方面,重構算法主要在傅立葉頻域進行,為了防止圖像邊緣突變引入的頻域誤差,需要對原始圖像的邊緣進行模糊,本申請實施例中,取原始圖像邊緣10個像素進行正弦模糊化處理。
步驟20:對預處理後的圖像進行頻譜分離,得到圖像的頻譜分量;
在步驟20中,頻譜分離具體為:根據平移相位,得到分離矩陣,根據公式(5)分別對每個方向上的3幅原始圖像進行分離,最終得到三個方向上的9個頻譜分量
步驟30:根據頻譜分量計算照明光的方向和空間頻率;
在步驟30中,由頻譜分量的表達式可知,樣品的零頻位於處,根據傅立葉變換性質,樣品的零頻值是時域圖像上所有像素的光強之和,即對於sim系統,照明光的空間頻率漂移較小,因此根據其空間頻率初始值和角度初始值設定濾波函數,對頻譜分量進行濾波,通過搜索確定濾波之後的數據的最大值,然後在最大值附近±1個像素的範圍內,採用質心法將峰值點位置精確到亞像素,進而得到照明光的方向和空間頻率。具體如圖3所示,為本申請實施例的頻譜分量濾波示意圖。由於頻譜的共軛性,只需要對m≥0的組分進行峰值點查找。該尋峰算法儘可能地排除了其他幹擾信息,在此基礎上進行峰值點查找,可以以提高空間頻率的求解精度。
步驟40:獲取sim成像系統的otf參數;
在步驟40中,otf在sim重構算法中是一個重要的參數,獲取otf的方法包括兩種:一種是採用螢光小球對sim成像系統進行標定,通過數據處理,得到psf,進而得到otf,這種方法可以反映真實的實驗系統,但是由於螢光信號較弱,測量數據受噪聲幹擾較大,且螢光小球並非理想點光源,所以很難得到效果較好的otf。另一種方法是採用psf理論模型,目前常用的psf理論模型有born&wolf模型、richard&wolf模型、gibson&lanni模型等。考慮到商用高精度物鏡的像差可以控制在很小的範圍內,本申請實施例中使用的psf理論模型是richard&wolf模型。模型中使用到的光學參數是根據實測的psf進行確定,以保證模型與實際系統更為接近。
步驟50:根據otf對頻譜分量進行參數修正,通過線性擬合算法計算照明光的調製度和初始相位,並通過照明光的調製度和初始相位將所有頻譜分量的係數歸一化為相同值;
在步驟50中,由公式(4)可知,每個頻譜分量的係數是不同的,因此需要對其進行歸一化,這樣才能通過各個頻譜的線性組合,獲得正確的樣品信息。本申請實施例對頻譜分量的係數進行歸一化的方式具體為:
(a)首先進行中心組分的匹配,由上述推導可知,中心組分(m=0)的表達式為:
假設b=s*a,則s=c1,0/cd,0,參數s可以通過對表達式a和b進行線性擬合得到,之後將所有其他組分用參數s進行修正,即:
其中表示將d1用d2替換。
(b)邊緣組分(m=±1)與中心組分進行匹配,根據傅立葉頻移定理:
將邊緣頻譜變換到實域,乘以相移因子然後再變換至頻域,得到移位之後的頻譜:
同樣地,可以獲得平移之後的otf,即這樣得到表達式a和b:
這兩個表達式在otf的重合區域應有相同的數值所以假設b=s*a,通過複數線性擬合得到參數如此,邊緣組分可以修正為:
對於m=1和m=-1,參數s是共軛的,因此只需要計算m=1時的參數。此時所有頻譜分量的參數都歸一化為c1,0。
考慮到噪聲和計算誤差,需要對表達式a和b中的數據進行篩選,然後再進行複數線性擬合計算。首先,傅立葉相移定理會引入不可避免的計算誤差,通過仿真分析證明該計算誤差對絕對值較小的數據的相位影響是顯著的,因此數據篩選的第一步是去掉絕對值過小的數據,即根據otf確定有效支持域。本申請實施例中,對於中心組分修正,所述支持域取|otf|>0.1的區域,對於邊緣組分修正,所述有效支持域為和的重疊區域。然後由有效支持域內a和b的數據組成數據對(ai,bi),雖然理論上數據bi與數據ai成正比,但是由於噪聲的存在,|bi|與|ai|的比值分布範圍較大,但大部分數值集中在一定區域內,所以選擇比值|bi|/|ai|分布在其最大概率附近的數據組作為有效數據。最後經過篩選的有效數據對(ai,bi)通過複數線性擬合用於參數s的估計,即
本申請實施例中通過將初始相位和調製度作為一個整體參數進行求解,在線性擬合算法的基礎上增加數據篩選功能,避免了繁瑣而耗時的自相關算法,同時可以降低誤差,提高計算精度。利用求解得到的參數對頻譜分量進行修正,最終將所有頻譜分量的係數歸一化為相同值。
步驟60:對頻譜分量進行去卷積和頻譜平移處理;
在步驟60中,對於光學成像系統,去卷積算法是提高解析度的重要手段。將每個未移位的頻譜分量分別乘以其對應的維納去卷積函數,得到濾波之後的頻譜組分為:
在公式(12)中,w是根據經驗調節的常數,一般與數據信噪比成反比。可見,此時樣品的零頻位於根據相移定理,將樣品的零頻移至正確位置,即得到:
需要注意的是,頻譜平移之後很可能會超過圖像所能容納的最大頻率(2×px)-1,其中px為像素大小。所以需要在頻域對圖像進行擴展。首先將n×n的頻域圖像周圍用0填充至2n×2n,這樣圖像能容納的最大頻率增加至px-1,足夠容納平移之後的頻譜。
步驟70:將所有平移至正確位置的頻譜分量進行加權組合,得到圖像的超分辨重構結果:
在公式(14)中,a(k)是切趾濾波函數,用於濾除高頻噪聲。對進行傅立葉逆變換得到時域的超分辨重構結果。
請參閱圖4,是本申請實施例的圖像重構系統的結構示意圖。本申請實施例的圖像重構系統包括圖像預處理模塊、頻譜分離模塊、照明光參數計算模塊、otf參數計算模塊、參數修正模塊、頻譜平移模塊和頻譜組合模塊;具體地:
圖像預處理模塊:用於對sim成像系統採集到的原始圖像進行預處理;在圖像採集過程中,由於相機曝光時間和照明光強的浮動,需要對測量序列中的所有原始圖像進行光強修正,保證每幅圖像的平均值相同。另一方面,重構算法主要在頻域進行,需要用到傅立葉變換,為了防止圖像邊緣突變引入的頻域誤差,需要對原始圖像的邊緣進行模糊,本申請實施例中,取10個像素對原始圖像的邊緣進行模糊化處理。
頻譜分離模塊:用於對預處理後的圖像進行頻譜分離,得到圖像的頻譜分量;其中,頻譜分離具體為:根據平移相位,得到分離矩陣,根據公式(5)分別對每個方向上的3幅原始圖像進行分離,最終得到三個方向上的9個頻譜分量
照明光參數計算模塊:用於根據頻譜分量計算照明光的方向和空間頻率;由頻譜分量的表達式可知,樣品的零頻位於處,根據傅立葉變換性質,樣品的零頻值是時域圖像上所有像素的光強之和,即對於sim系統,照明光的空間頻率漂移較小,因此根據其空間頻率初始值和角度初始值設定濾波函數,對頻譜分量進行濾波,通過搜索確定濾波之後的數據的最大值,然後在最大值附近±1個像素的範圍內,採用質心法將峰值點位置精確到亞像素,進而得到照明光的方向和空間頻率。由於頻譜的共軛性,只需要對m≥0的組分進行峰值點查找。可以儘可能地排除其他幹擾,提取出有用的信息量,在此基礎上進行峰值點查找,以提高空間頻率的求解精度。
otf參數計算模塊:用於獲取sim成像系統的otf參數;otf在sim重構算法中是一個重要的參數,獲取otf參數的方法包括兩種:一種是採用螢光小球對sim成像系統進行標定,通過數據處理,得到psf,進而得到otf,這種方法可以反映真實的實驗系統,但是由於螢光信號較弱,測量數據受噪聲幹擾較大,且螢光小球並非理想點光源,所以很難得到效果較好的otf。另一種方法是採用psf理論模型,目前常用的psf理論模型有born&wolf模型、richard&wolf模型、gibson&lanni模型等。考慮到商用高精度物鏡的像差可以控制在很小的範圍內,本申請實施例中使用的psf理論模型是richard&wolf模型。模型中使用到的參數是根據實測的psf進行確定,以保證模型與實際系統更為接近。
參數修正模塊:用於通過線性擬合算法計算照明光的調製度和初始相位,通過照明光的調製度和初始相位對頻譜分量進行修正,將所有頻譜分量的係數歸一化為相同值;其中,由公式(4)可知,每個頻譜分量的係數是不同的,因此需要對其進行歸一化,這樣才能通過各個頻譜的線性組合,獲得正確的樣品信息。本申請實施例對頻譜分量的係數進行歸一化的方式具體為:
(a)首先進行中心組分的匹配,由上述推倒可知,中心組分(m=0)的表達式為:
假設b=s*a,則s=c1,0/cd,0,參數s可以通過對表達式a和b進行線性擬合得到,之後將所有其他組分用參數s進行修正,即:
其中表示將d1用d2替換。
(b)邊緣組分(m=±1)與中心組分進行匹配,根據傅立葉頻移定理:
將邊緣頻譜變換到實域,乘以相移因子然後再變換至頻域,得到移位之後的頻譜:
同樣地,可以獲得平移之後的otf,即這樣得到表達式a和b:
這兩個表達式在otf的重合區域應有相同的數值所以假設b=s*a,通過複數線性擬合得到參數如此,邊緣組分可以修正為:
對於m=1和m=-1,參數s是共軛的,因此只需要計算m=1時的參數。此時所有頻譜分量的參數都歸一化為c1,0。
參數修正中使用到的線性擬合算法的步驟為:首先計算表達式a和b的有效支持域,一般取|otf|>0.1的區域,如公式(10)所述,有效支持域為和的重疊區域;然後由有效支持域內a和b的數據組成數據對(ai,bi),由於噪聲和計算誤差的存在,需要對數據對(ai,bi)進行數據篩選,得到有效數據對,以提高計算精度,數據篩選過程主要包括:
(i)傅立葉相移定理會引入不可避免的計算誤差,通過仿真證明該計算誤差對絕對值較小的數據的相位影響是顯著的,因此數據篩選的第一步是去掉絕對值過小的數據;
(ii)雖然理論上數據bi與數據ai成正比,但是由於噪聲的存在,|bi|與|ai|的比值分布範圍較大,但大部分數值集中在一定區域內,所以選擇比值|bi|/|ai|分布在其最大概率附近的數據組作為有效數據。經過篩選的有效數據對(ai,bi)通過複數線性擬合用於參數s的估計,即
本申請實施例中通過將初始相位和調製度作為一個整體參數進行求解,在線性擬合算法的基礎上增加數據篩選功能,避免了繁瑣而耗時的自相關算法,同時可以降低誤差,提高計算精度。利用求解得到的參數對頻譜分量進行修正,最終將所有頻譜分量的係數歸一化為相同值。
頻譜平移模塊:用於對頻譜分量進行去卷積和頻譜平移處理;對於光學成像系統,去卷積算法是提高解析度的重要手段。將每個未移位的頻譜分量分別乘以其對應的維納去卷積函數,得到濾波之後的頻譜組分為:
在公式(12)中,w是根據經驗調節的常數,一般與數據信噪比成反比。可見,此時樣品的零頻位於根據相移定理,將樣品的零頻移至正確位置,即得到:
需要注意的是,頻譜平移之後很可能會超過圖像所能容納的最大頻率(2×px)-1,其中px為像素大小。所以需要在頻域對圖像進行擴展。首先將n×n的頻域圖像周圍用0填充至2n×2n,這樣圖像能容納的最大頻率增加至px-1,足夠容納平移之後的頻譜。
頻譜組合模塊:用於將所有平移至正確位置的頻譜分量進行加權組合,得到圖像的超分辨重構結果:
在公式(14)中,a(k)是切趾濾波函數,用於濾除高頻噪聲。對進行傅立葉逆變換得到時域的超分辨重構結果。
實例說明:
採用本申請實施例的圖像重構算法對sim原始圖像(來自geomx)進行重構,得到的圖像重構結果如圖5所示,為本申請實施例的圖像重構結果示意圖。圖示的左下角圖像是黑色方框內的放大圖,標尺為4um。其中,圖5(a)表示無參數修正部分的圖像重構結果;圖5(b)表示有參數修正部分的圖像重構結果;圖5(c)表示寬場成像結果。對比圖5(a)和圖5(b)可知,參數修正部分是算法中必不可少的一項,對重構圖像的質量有重要影響。對比圖5(b)和圖5(c)可知,本申請實施例的圖像重構算法可有效提高系統解析度。
本申請實施例的圖像重構方法及系統利用理想相位對預處理圖像進行頻譜分離,根據照明光空間頻率初始值設定濾波函數,對分離頻譜進行濾波,再進行峰值點搜索,並通過質心法將峰值點的定位精度提高至亞像素級,以確定照明光的空間頻率。採用簡單而有效的線性擬合算法求解照明光的調製度和初始相位,並在此基礎上增加數據篩選功能,避免了繁瑣而耗時的互相關算法,同時又提高了求解精度;並利用計算得到的調製度和初始相位對頻譜分量進行參數歸一化,從而有效提高重構圖像的質量。
對所公開的實施例的上述說明,使本領域專業技術人員能夠實現或使用本申請。對這些實施例的多種修改對本領域的專業技術人員來說將是顯而易見的,本文中所定義的一般原理可以在不脫離本申請的精神或範圍的情況下,在其它實施例中實現。因此,本申請將不會被限制於本文所示的這些實施例,而是要符合與本文所公開的原理和新穎特點相一致的最寬的範圍。
