基於Galerkin條形傳遞函數的薄板振動特性分析方法與流程
2023-05-19 03:31:11
本發明涉及彈性力學領域,具體涉及一種基於Galerkin條形傳遞函數的薄板振動特性分析方法。
背景技術:
在彈性力學中,只有極少數問題能夠給出解析解,大多數問題需要通過數值方法來求解,Kirchhoff板振動特性的求解亦如此。在眾多數值方法中,有限元法最常見,也是最實用的一種方法。有限元法最大的優點是不受求解區域、邊界條件以及材料屬性的限制,可以分析具有複雜幾何形狀的彈性力學問題。但是,有限元方法計算量大,計算時間長,對計算機性能要求高。特別是對某些特殊問題,如彈性體的主動控制的實時計算問題,高梯度應力分布的求解問題,以及高頻動態響應計算問題等,有限元法求解精度不高。
條形傳遞函數方法是一種求解二維彈性力學問題的半解析數值方法。這種方法的思想類似於有限條法,也是將求解區域分為若干個條形區域,稱為條形單元,在條形單元內利用多項式和連續函數近似橫向和縱向位移,從而得到基於條形單元的整體微分方程,最後利用傳遞函數方法求解微分方程,得到半解析解。該方法的一個顯著優點是,其既具有有限元方法的靈活性,可以分析複雜形狀的幾何區域,同時又能給出封閉形式的高精度半解析解。然而,傳統的條形傳遞函數方法基於Hamilton原理,需要先給出待求問題對應的能量泛函。而問題是,並非所有問題都可以很容易地給出其相應的能量泛函,如基於微分型非局部本構模型的薄板彎曲問題,這使得條形傳遞函數方法的應用受到了限制。然而,Galerkin方法不需要先寫出待研究問題的能量泛函,可以直接對微分方程進行近似求解。
技術實現要素:
本發明要解決的技術問題:針對現有技術的上述問題,提供一種求解精度高、計算過程數據存儲量少、計算效率高的基於Galerkin條形傳遞函數的薄板振動特性分析方法。
為了解決上述技術問題,本發明採用的技術方案為:
一種基於Galerkin條形傳遞函數的薄板振動特性分析方法,其步驟包括:
1)將薄板上給定的矩形區域用NE+1條結線劃分為NE個矩形區域,每一個矩形區域為一個條形單元,第j個條形單元包含第j條結線和第j+1條結線以及4個節點;
2)選取形函數矩陣N(y),分別根據選取的形函數矩陣N(y)計算每一個條形單元的剛度陣質量陣me以及荷載向量fe;
3)基於每一個條形單元的剛度陣質量陣me以及荷載向量fe組裝總體 運動微分方程,並針對所述總體運動微分方程處理邊界條件;
4)計算所述總體運動微分方程的傳遞矩陣F(s)以及邊界矩陣Mb(s)與Nb(s);
5)根據傳遞矩陣F(s)以及邊界矩陣Mb(s)與Nb(s)計算固有頻率ω。
優選地,所述步驟1)中第j個條形單元的結線位移函數向量如式(1)所示;第j個條形單元的橫向位移函數可以通過插值表示如式(2)所示;
φ(x,t)={wj θj wj+1 θj+1}T (1)
式(1)中,φ(x,t)為第j個條形單元的結線位移函數向量,wj為第j條結線的位移,θj為第j條結線的轉角,wj+1為第j+1條結線的位移,θj+1為第j+1條結線的轉角;
w(x,y,t)=N(y)φ(x,t) (2)
式(2)中,w(x,y,t)為第j個條形單元的橫向位移函數,φ(x,t)為第j個條形單元的結線位移函數向量,N(y)為形函數矩陣。
優選地,所述步驟2)中選取的形函數矩陣N(y)為標準Euler梁單元的形函數。
優選地,所述步驟2)中剛度陣的計算函數表達式如式(3)所示;
式(3)中,為條形單元剛度矩陣,y為條形單元的寬度方向坐標軸,l為條形單元的寬度,D為薄板的彎曲剛度,N為選取的形函數矩陣N(y),v為薄板的泊松比。
優選地,所述步驟2)中質量陣me的計算函數表達式如式(4)所示;
式(4)中,me為條形單元的質量陣,l為條形單元的寬度,ρ為薄板的密度,h為為薄板的厚度,N為選取的形函數矩陣,y為條形單元的寬度方向坐標軸。
優選地,所述步驟2)中荷載向量fe的計算函數表達式如式(5)所示;
式(5)中,fe為條形單元的荷載向量;為容許函數,容許函數為選取的形函數矩陣N的轉置矩陣NT,為條形單元結線上的等效剪力,My為條形單元結線上的y方向彎矩,l為條形單元的寬度。
優選地,所述步驟3)中組裝的總體運動微分方程如式(6)所示;
式(6)中,為總體剛度陣,分別由條形單元的剛度矩陣組裝而成,M為由條形單元質量陣me組成的總體質量陣,F為由條形單元荷載向量fe組成的總體荷載向量,Φ(x,t)為由條形單元結線位移函數向量組裝而成的總體位移向量,總體位移向量Φ(x,t)的函數表達式如式(7)所示;
Φ(x,t)={w1(x,t) θ1(x,t) w2(x,t) θ2(x,t) … wNE(x,t) θNE(x,t)}T (7)
式(7)中,Φ(x,t)為總體位移向量,wNE(x,t)為第NE條結線的位移,θNE(x,t)為第NE條結線的轉角。
優選地,所述步驟3)中基於每一個條形單元的剛度陣質量陣me以及荷載向量fe組成的總體運動微分方程處理邊界條件後如式(8)所示;
式(8)中,分別為處理邊界條件後得到的總體剛度陣,為處理邊界條件後得到的總體質量陣,為處理邊界條件後得到的總體荷載向量,為處理邊界條件後的總體位移向量。
優選地,所述步驟4)的詳細步驟包括:
4.1)採用式(9)所示函數表達式計算所述總體運動微分方程的傳遞矩陣F(s);
式(9)中,I為單位陣,D(s)和D2的函數表達式如式(10)所示;
式(10)中,分別為處理邊界條件後得到的總體剛度陣,為處理邊界條件後得到的總體質量陣,s為Laplace變換係數;
4.2)判斷薄板的邊界類型,如果邊界類型為簡支邊界條件,則根據式(11)計算總體運動微分方程的邊界矩陣Mb(s)與Nb(s);否則如果邊界類型為固支邊界條件,則根據式(12)計算總體運動微分方程的邊界矩陣Mb(s)與Nb(s);
式(11)中,Mb(s)與Nb(s)分別為總體運動微分方程的邊界矩陣,為N1階單位陣,N1為未知位移個數。
式(12)中,Mb(s)與Nb(s)分別為總體運動微分方程的邊界矩陣,為N1階單位陣,N1為未知位移個數。
優選地,所述步驟5)中計算薄板自由振動的固有頻率ω的函數表達式如式(13)所示;
det(Mb(iω)e-0.5aF(iω)+Nb(iω)e0.5aF(iω))=0 (13)
式(13)中,Mb(s)與Nb(s)分別為總體運動微分方程的邊界矩陣,F(s)為總體運動微分方程的傳遞矩陣,a為條形單元長度,det為行列式符號,i為虛數單位。
本發明基於Galerkin條形傳遞函數的薄板振動特性分析方法具有下述優點:
1、本發明直接從薄板平衡方程出發,利用虛功原理,建立條形單元的運動微分方程,不需要給出薄板對應的能量泛函,適用性更廣,計算更簡便;
2、本發明相對於有限元方法,Galerkin條形傳遞函數方法在空間的一個方向給出了解析解,在整個空間上給出了半解析解,從而可以顯著地提高求解精度和求解效率;
3、本發明方法解的形式統一,易於利用計算機編程,並且可以用於相對較複雜的幾何區域以及邊界條件問題的求解。
4、本發明直接從薄板平衡方程出發,利用虛功原理,建立條形單元的運動微分方程,不需要給出薄板對應的能量泛函,不僅適用於基於Galerkin條形傳遞函數的薄板振動特性分析方法,而且同樣也可用於其他難以直接寫出能量泛函的二維數學物理問題的求解。
附圖說明
圖1為本發明實施例方法的基本流程示意圖。
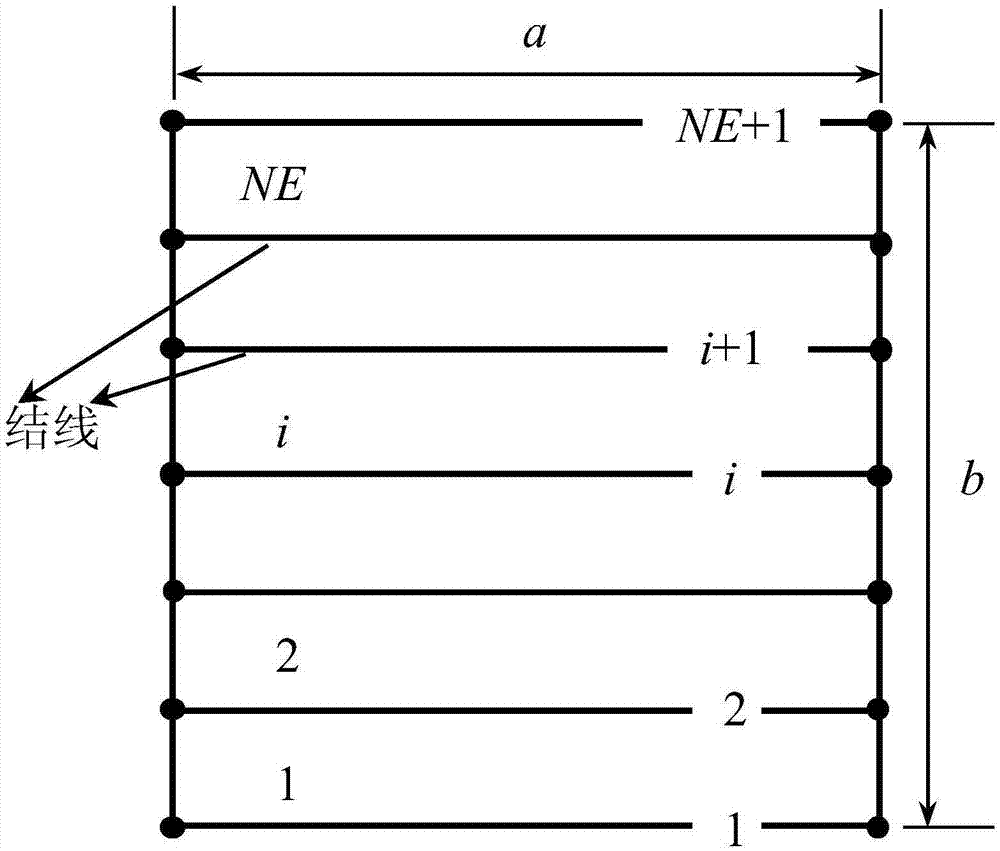
圖2為本發明實施例中給定的矩形區域劃分原理示意圖。
圖3為本發明實施例中某一個條形單元的結構示意圖。
具體實施方式
如圖1所示,本實施例基於Galerkin條形傳遞函數的薄板振動特性分析方法的步驟包括:
1)將薄板上給定的矩形區域用NE+1條結線劃分為NE個矩形區域,每一個矩形區域為一個條形單元,第j個條形單元包含第j條結線和第j+1條結線以及4個節點;參見圖2和圖3,本實施例中給定的矩形區域長度為a、總寬度為b,用NE+1條結線劃分為NE個矩形區域後,每一個條形單元的寬度為l,Oxy為條形單元局部坐標系;
2)選取形函數矩陣N(y),分別根據選取的形函數矩陣N(y)計算每一個條形單元的剛度陣質量陣me以及荷載向量fe;
3)基於每一個條形單元的剛度陣質量陣me以及荷載向量fe組裝總體運動微分方程,並針對總體運動微分方程處理邊界條件;
4)計算總體運動微分方程的傳遞矩陣F(s)以及邊界矩陣Mb(s)與Nb(s);
5)根據傳遞矩陣F(s)以及邊界矩陣Mb(s)與Nb(s)計算固有頻率ω。
本實施例中,步驟1)中第j個條形單元的結線位移函數向量如式(1)所示;第j個條形單元的橫向位移函數可以通過插值表示如式(2)所示;
φ(x,t)={wj θj wj+1 θj+1}T (1)
式(1)中,φ(x,t)為第j個條形單元的結線位移函數向量,wj為第j條結線的位移,θj為第j條結線的轉角,wj+1為第j+1條結線的位移,θj+1為第j+1條結線的轉角;
w(x,y,t)=N(y)φ(x,t) (2)
式(2)中,w(x,y,t)為第j個條形單元的橫向位移函數,φ(x,t)為第j個條形單元的結線位移函數向量,N(y)為形函數矩陣。
本實施例中,步驟2)中選取的形函數矩陣N(y)為標準Euler梁單元的形函數,其表達式具體為N=[N1 N2 N3 N4]。
本實施例中,步驟2)中剛度陣的計算函數表達式如式(3)所示;
式(3)中,為條形單元剛度矩陣,y為條形單元的寬度方向坐標軸,l為條形單元的寬度,D為薄板的彎曲剛度,N為選取的形函數矩陣N(y),v為薄板的泊松比。
本實施例中,步驟2)中質量陣me的計算函數表達式如式(4)所示;
式(4)中,me為條形單元的質量陣,l為條形單元的寬度,ρ為薄板的密度,h為為薄板的厚度,N為選取的形函數矩陣,y為條形單元的寬度方向坐標軸。
本實施例中,步驟2)中荷載向量fe的計算函數表達式如式(5)所示;
式(5)中,fe為條形單元的荷載向量,為容許函數,容許函數為選取的形函數矩陣N的轉置矩陣NT,為條形單元結線上的等效剪力,My為條形單元結線上的y方向彎矩,l為條形單元的寬度。
對於圖3所示的每個條形單元,用彎矩和扭矩表示的動力學方程如式(5-1)所示;
式(5-1)中,ρ為薄板的密度,h為為薄板的厚度,w為條形單元的位移,Mx為薄板的x方向彎矩,My為薄板的y方向彎矩,Mxy為薄板的扭矩,如式(5-2)所示;
式(5-2)中,D為彈性矩陣,其餘符號參數與式(5-1)相同,彈性矩陣D的具體形式如式(5-3)所示;
式(5-3)中,D為彈性矩陣,D為薄板的彎曲剛度,v為薄板的泊松比。
條形單元上下邊界分別作用等效剪力與彎矩如式(5-4)所示;
式(5-4)中,為剪力,為條形單元結線上的等效剪力,My為條形單元結線上的彎矩,Mxy為條形單元結線上的扭矩,l為條形單元的寬度。
式(5-1)所示動力學方程在y方向上的等效積分「弱」形式如式(5-5)所示;
式(5-5)中,為權函數,Mx為條形單元結線上的x方向彎矩,My為條形單元結線上的y方向彎矩,Mxy為條形單元結線上的扭矩,l為條形單元的寬度。
式(5-5)等於式(5-6)所示函數表達式;
式(5-6)中,各個字符參數含義與式(5-5)相同。
將式(5-2)代入式(5-6),且令條形單元的位移w等於形函數N(y)和橫向位移函數的乘積φ(x,t)(即w=N(y)φ(x,t)),權函數為選取的形函數矩陣N的轉置矩陣NT即可得到式(5-7);
式(5-7)中,D為薄板的彎曲剛度,v為薄板的泊松比,N為選取的形函數矩陣,ρ為薄板的密度,h為為薄板的厚度,x為條形單元的長度方向坐標軸,y為條形單元的寬度方向坐標軸,為容許函數,容許函數為選取的形函數矩陣N的轉置矩陣NT,l為條形單元的寬度,φ為處理邊界條件後的總體位移。
式(5-7)可記為式(5-8)所示函數表達式;
式(5-8)中,為條形單元的剛度矩陣,me為條形單元的質量陣,fe為條形單元的荷載向量,φ為處理邊界條件後的總體位移。式(5-8)中剛度陣的計算函數表達式如式(3)所示,質量陣me的計算函數表達式如式(4)所示,荷載向量fe的計算函數表達式如式(5)所示。
本實施例中,本實施例中,步驟3)中組裝的總體運動微分方程時,將單元剛度矩陣組裝成總體剛度陣的過程和有限元法相同,總體運動微分方程如式(6)所示;
式(6)中,K(4)、K(2)、K(0)為總體剛度陣,分別由條形單元的剛度矩陣組裝而成,M為由條形單元質量陣me組成的總體質量陣,F為由條形單元荷載向量fe組成的總體荷載向量,Φ(x,t)為由條形單元結線位移函數向量組裝而成的總體位移向量,總體位移向量Φ(x,t)的函數表達式如式(7)所示;
Φ(x,t)={w1(x,t) θ1(x,t) w2(x,t) θ2(x,t) … wNE(x,t) θNE(x,t)}T (7)
式(7)中,Φ(x,t)為總體位移向量,wNE(x,t)為第NE條結線的位移,θNE(x,t)為第NE條結線的轉角。
本實施例中,步驟3)中基於每一個條形單元的剛度陣質量陣me以及荷載向量fe組成的總體運動微分方程處理邊界條件後如式(8)所示;
式(8)中,分別為處理邊界條件後得到的總體剛度陣,為處理邊界條件後得到的總體質量陣,為處理邊界條件後得到的總體荷載向量,為處理邊界條件後的總體位移向量。
本實施例中,步驟4)的詳細步驟包括:
4.1)採用式(9)所示函數表達式計算總體運動微分方程的傳遞矩陣F(s);
式(9)中,I為單位陣,D(s)和D2的函數表達式如式(10)所示;
式(10)中,分別為處理邊界條件後得到的總體剛度陣,為處理邊界條件後得到的總體質量陣,s為Laplace變換係數;
4.2)判斷薄板的邊界類型,如果邊界類型為簡支邊界條件,則根據式(11)計算總體運動微分方程的邊界矩陣Mb(s)與Nb(s);否則如果邊界類型為固支邊界條件,則根據式(12)計算總體運動微分方程的邊界矩陣Mb(s)與Nb(s);
式(11)中,Mb(s)與Nb(s)分別為總體運動微分方程的邊界矩陣,為N1階單位陣,N1為未知位移個數。
式(12)中,Mb(s)與Nb(s)分別為總體運動微分方程的邊界矩陣,為N1階單位陣,N1為未知位移個數。
本實施例中,步驟5)中計算薄板自由振動的固有頻率ω的函數表達式如式(13)所示;
det(Mb(iω)e-0.5aF(iω)+Nb(iω)e0.5aF(iω))=0 (13)
式(13)中,Mb(s)與Nb(s)分別為總體運動微分方程的邊界矩陣,F(s)為總體運動微分方程的傳遞矩陣,a為條形單元長度,det為行列式符號,i為虛數單位。
如式(8)所示總體運動微分方程取時間的Laplace變化可得式(13-1);
式(13-1)中,分別為處理邊界條件後得到的總體剛度陣,為處理邊界條件後得到的總體質量陣,為處理邊界條件後的總體位移向量的Laplace變換,為處理邊界條件後得到的總體荷載向量的Laplace變換,s為Laplace變換係數。
對於薄板的自由振動,總體荷載向量的Laplace變換因此可得式(13-2);
式(13-2)中,為處理邊界條件後的總體位移向量的Laplace變換,D(s)和D2的函數表達式可參見式(10)。
定義狀態向量η(x,s)如式(13-3)所示;
則式(13-2)可寫成式(13-4)所示函數表達式;
式(13-4)中,η(x,s)為定義的狀態向量,F(s)為狀態矩陣,如式(9)所示。基於式(13-4),即可推導得出左右邊界條件如式(13-5)所示。
Mb(s)η(-0.5a)+Nb(s)η(0.5a)=0 (13-5)
式(13-5)中,Mb(s)與Nb(s)稱為邊界矩陣,a為條形單元的長度。判斷薄板的邊界類型,如果邊界類型為簡支邊界條件,則根據式(11)計算總體運動微分方程的邊界矩陣Mb(s)與Nb(s);否則如果邊界類型為固支邊界條件,則根據式(12)計算總體運動微分方程的邊界矩陣Mb(s)與Nb(s)。
求解式(13-4)和式(13-5),即可得到如式(13-6)所示的解;
η(x,s)=exF(s)(Mb(s)e-0.5aF(s)+Nb(s)e0.5aF(s))-1(13-6)
式(13-6)中,η(x,s)為定義的狀態向量,F(s)為狀態矩陣,a為條形單元的長度,Mb(s)與Nb(s)稱為邊界矩陣,最終可推導出式(13-6)的特徵方程如式(13)所示。在式(13)所示特徵方程的基礎上,令s=iω,i為虛數單位,則ω即為薄板自由振動的固有頻率。
綜上所述,本實施例將Galerkin方法與條形傳遞函數方法相結合,提出了用於薄板振動特性問題的求解的Galerkin條形傳遞函數方法,為求解薄板振動特性問題提供一種精度高、計算速度快的新方法。
以上所述僅是本發明的優選實施方式,本發明的保護範圍並不僅局限於上述實施例,凡屬於本發明思路下的技術方案均屬於本發明的保護範圍。應當指出,對於本技術領域的普通技術人員來說,在不脫離本發明原理前提下的若干改進和潤飾,這些改進和潤飾也應視為本發明的保護範圍。
