基於Adaboost聚類和馬爾科夫鏈的分布式光伏超短期預測方法與流程
2023-05-05 20:39:46 3
本發明屬於分布式光伏發電系統技術領域,尤其涉及一種基於Adaboost聚類和馬爾科夫鏈的分布式光伏超短期預測方法。
背景技術:
近年來光伏發電裝機容量不斷增加,其波動性和間歇性對電力系統運行造成的衝擊日漸突出。分布式光伏的超短期預測對電力系統安全經濟運行有重要意義,主要體現為兩個方面:第一,基於預測功率制定控制策略,降低光伏併網時功率波動對電力系統的影響,提高系統的安全性、可靠性及可控性;第二,有助於電力系統調度部門確定機組出力計劃,降低系統內旋轉備用,減少用電成本。在滿足安全穩定的前提條件下,最大限度地消納可再生能源逐漸成為光伏發電研究領域的重點,故功率預測對分布的以及併網的光伏發電系統的大規模發展具有實用價值。
光伏輸出功率在地表光照強度的影響下表現出隨機性和波動性,不同天氣類型下,光伏輸出功率變化規律存在明顯的差異,因此在實際應用中難以使用統一的預測模型對各氣象條件下的光伏出力進行預測。聚類預測是通過對輸入數據進行特徵提取及數據挖掘的組合預測方法,與單一預測方法相比能提高預測精度。由於高成本數值天氣預報難以廣泛應用於分布式光伏預測系統,當前大多數研究採用基於天氣預報信息及雲量信息對不同類型數據進行分類的組合預測方法,沒有充分挖掘歷史太陽輻射強度信息,預測精度在天氣預報不準確的情況下顯著下降。
技術實現要素:
本發明的目的是提供一種基於Adaboost聚類和馬爾科夫鏈的組合預測方法,不僅在晴朗天氣下能取得較好的預測效果,還提高了非晴朗天氣下的預測精度。
為實現上述目的,本發明採用的技術方案是:基於Adaboost聚類和馬爾科夫鏈的分布式光伏超短期預測方法,包括以下步驟:
步驟1、採用滑動平均法提取光照強度序列的確定性分量,統計分析得到不同天氣類型的光照強度衰減因子;
步驟2、採用Adaboost改進的KNN方法對歷史數據進行聚類分析,建立分類預測模型;
步驟3、採用多階加權馬爾科夫鏈方法預測地表太陽輻照度;
步驟4、建立光電轉換模型,完成光伏功率超短期預測。
在上述的基於Adaboost聚類和馬爾科夫鏈的分布式光伏超短期預測方法中,步驟1的實現包括:
1.1採用滑動平均法濾除光照強度的隨機波動分量,提取確定性分量並選擇該分量作為聚類分析的特徵變量;
(1)式中yt為原始光照強度實測值,m選擇滑動平均時間窗口,Yt為平滑處理後的滑動平均值;
1.2根據天文日地關係計算地表太陽輻照度Hottel標準晴天理論值,將歷史數據與對應標準晴天理論值進行對比統計,得到不同天氣類型的光照強度衰減因子經驗值並輸入預測模型;
(2)式中,Imea(i)第i時刻地表光照強度,Istd(i)Hottel標準晴天理論值,m為衰減因子。
在上述的基於Adaboost聚類和馬爾科夫鏈的分布式光伏超短期預測方法中,步驟2的實現包括:
2.1採用k-means聚類,通過設置聚類中心個數k、選擇初始聚類中心,並在每次迭代中將樣本歸為距離最近的中心所屬類別,每次迭代後重新根據類別中的樣本更新聚類中心,直至前後兩次中心的變化不超過設置值或者迭代次數小於設置值;
2.2採用KNN分類算法,通過此時k個最鄰近樣本的類別所佔比例中最大的類別作為未知對象的類別;或者根據距離遠近對鄰近類別加權選擇結果最大的類別作為未知對象的類別;
2.3採用Adaboost算法,通過訓練數據學習得到某種弱分類器Gm(x),通過對弱分類器的組合得到強分類器,即強分類器可以表示為:
(3)式中αm為第m次計算得到的弱分類器在強分類器中的加權值。
在上述的基於Adaboost聚類和馬爾科夫鏈的分布式光伏超短期預測方法中,步驟3的實現包括:
3.1對歷史數據預處理,獲得誤差百分數序列,定義相對預測誤差eit為:
(4)式中為光照強度預測值,為光照強度實際值,i為每日的預測點數;N為樣本數;
3.2狀態劃分,研究對象為Hottel標準晴天模型值與實際值之間的誤差,將預處理中得到的誤差百分數按實際運行經驗劃分為11個離散狀態,其中誤差小於-5%的點定義為狀態1,相鄰兩狀態的誤差級差為10%,依次類推,誤差大於85%的點定義為狀態11;
3.3求取狀態轉移概率矩陣;
在m時刻太陽輻射的狀態為Si轉移到m+k時刻太陽輻射的狀態為Sj的轉移概率為:
利用上述狀態劃分的結果,統計出各個步長(階數k不同)狀態變化的轉移頻數矩陣:
3.4計算各階影響權重;
誤差序列k階自相關係數計算公式如下:
(7)式中xi表示第i時段的誤差,為平均誤差,n為時間長度;
由(7)式求得的各階自相關係數計算各階影響權重:
3.5地表光照強度預測;
得到的不同步長的狀態轉移概率矩陣後,由預測日某時段誤差百分數所在狀態預測出下一採樣時刻誤差百分數所在某一狀態的概率,並取得概率最大的一個狀態為預測誤差狀態,從而得到對應的相對預測誤差值e(t);計算地表光照強度預測值:
Ipre(t)=Istd(t)×(1-e(t)) (9);
(9)式中,Ipre(t)為t時刻地表光照強度預測值,Istd(t)為t時刻標準晴天理論值,e(t)為預測計算用誤差百分數。
在上述的基於Adaboost聚類和馬爾科夫鏈的分布式光伏超短期預測方法中,步驟4的實現包括:
採用間接預測法,得到光照強度的預測數值後,通過光電轉換模型計算光伏輸出功率,計算公式為:
P=ηSI[1-0.005(t0+25)] (10);
(10)式中,η是光電轉換效率,S是用於光伏發電的有效總面積,I(t)是接收到的有效光照強度,t0為光伏電池的工作溫度。
本發明的有益效果是:本發明提出了基於Adaboost聚類和馬爾科夫鏈的組合預測方法,該方法不僅在晴朗天氣下能取得較好的預測效果,還提高了非晴朗天氣下的預測精度。Adaboost改進的K近鄰(KNN)算法不需要提前知道誤差邊界,具有自適應性,能加強弱分類器對不平衡數據集的分類效果。馬爾科夫鏈(Markov Chain)是通過劃分狀態並使用狀態之間的概率轉移過程預測系統之後可能的發展趨勢和確定未知狀態,適用於對隨機不確定事件進行跟蹤預測。引入不同天氣類型光照強度衰減因子,可以放大預測誤差中的變化細節,並將幅值相對于晴空模型值較小的誤差變化反映出來,顯著提高了陰雨天氣類型下地表光照強度的預測精度。綜合多因素多步建模,具有較廣的適用範圍,採用工程經驗建立光電轉換模型簡化了功率預測問題。
附圖說明
圖1是本發明一個實施例的超短期預測方法流程圖;
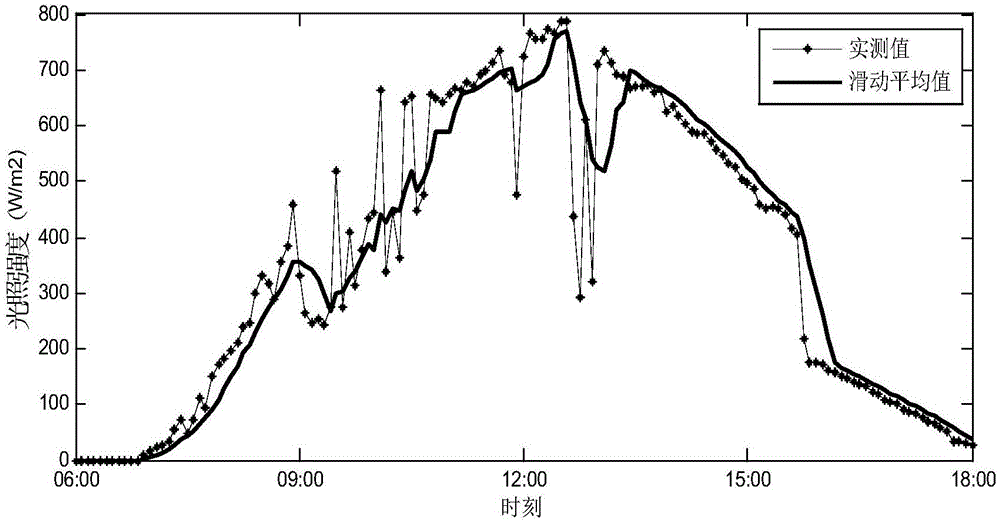
圖2是本發明一個實施例滑動平均確定性變量的提取圖;
圖3是本發明一個實施例光照強度衰減值的區間分布圖;
圖4是本發明一個實施例地表光照強度的四類聚類中心圖;
圖5是本發明一個實施例典型日實測光照強度和標準晴天光照強度對比曲線;
圖6是本發明一個實施例晴天下的模型和傳統馬爾科夫鏈的預測對比曲線;
圖7是本發明一個實施例多雲下的模型和傳統馬爾科夫鏈的預測對比曲線;
圖8是本發明一個實施例雨天下的模型和傳統馬爾科夫鏈的預測對比曲線;
圖9是本發明一個實施例陰天下的模型和傳統馬爾科夫鏈的預測對比曲線;
具體實施方式
下面結合附圖對本發明的實施方式進行詳細描述。
所述實施例的示例在附圖中示出,其中自始至終相同或類似的標號表示相同或類似的元件或具有相同或類似功能的元件。下面通過參考附圖描述的實施例是示例性的,僅用於解釋本發明,而不能解釋為對本發明的限制。
實施例採用如下技術方案:基於Adaboost聚類和馬爾科夫鏈的分布式光伏超短期預測方法,包括以下步驟:
步驟1、採用滑動平均法提取光照強度序列的確定性分量,統計分析得到不同天氣類型的光照強度衰減因子;
步驟2、採用Adaboost改進的KNN方法對歷史數據進行聚類分析,建立分類預測模型;
步驟3、採用多階加權馬爾科夫鏈方法預測地表太陽輻照度;
步驟4、建立光電轉換模型,完成光伏功率超短期預測。
進一步,步驟1的實現包括:
1.1採用滑動平均法濾除光照強度的隨機波動分量,提取確定性分量並選擇該分量作為聚類分析的特徵變量;
(1)式中yt為原始光照強度實測值,m選擇滑動平均時間窗口,Yt為平滑處理後的滑動平均值;
1.2根據天文日地關係計算地表太陽輻照度Hottel標準晴天理論值,將歷史數據與對應標準晴天理論值進行對比統計,得到不同天氣類型的光照強度衰減因子經驗值並輸入預測模型;
(2)式中,Imea(i)第i時刻地表光照強度,Istd(i)Hottel標準晴天理論值,m為衰減因子。
進一步,步驟2的實現包括:
2.1採用k-means聚類,通過設置聚類中心個數k、選擇初始聚類中心,並在每次迭代中將樣本歸為距離最近的中心所屬類別,每次迭代後重新根據類別中的樣本更新聚類中心,直至前後兩次中心的變化不超過設置值或者迭代次數小於設置值;
2.2採用KNN分類算法,通過此時k個最鄰近樣本的類別所佔比例中最大的類別作為未知對象的類別;或者根據距離遠近對鄰近類別加權選擇結果最大的類別作為未知對象的類別;
2.3採用Adaboost算法,通過訓練數據學習得到某種弱分類器Gm(x),通過對弱分類器的組合得到強分類器,即強分類器可以表示為:
(3)式中αm為第m次計算得到的弱分類器在強分類器中的加權值。
進一步,步驟3的實現包括:
3.1對歷史數據預處理,獲得誤差百分數序列,定義相對預測誤差eit為:
(4)式中為光照強度預測值;為光照強度實際值;i為每日的預測點數;N為樣本數;
3.2狀態劃分,研究對象為Hottel標準晴天模型值與實際值之間的誤差,將預處理中得到的誤差百分數按實際運行經驗劃分為11個離散狀態,其中誤差小於-5%的點定義為狀態1,相鄰兩狀態的誤差級差為10%,依次類推,誤差大於85%的點定義為狀態11;
3.3求取狀態轉移概率矩陣;
在m時刻太陽輻射的狀態為Si轉移到m+k時刻太陽輻射的狀態為Sj的轉移概率為:
利用上述狀態劃分的結果,統計出各個步長(階數k不同)狀態變化的轉移頻數矩陣:
3.4計算各階影響權重;
誤差序列k階自相關係數計算公式如下:
(7)式中xi表示第i時段的誤差,為平均誤差,n為時間長度;
由(7)式求得的各階自相關係數計算各階影響權重:
3.5地表光照強度預測;
得到的不同步長的狀態轉移概率矩陣後,由預測日某時段誤差百分數所在狀態預測出下一採樣時刻誤差百分數所在某一狀態的概率,並取得概率最大的一個狀態為預測誤差狀態,從而得到對應的相對預測誤差值e(t);計算地表光照強度預測值:
Ipre(t)=Istd(t)×(1-e(t)) (9);
(9)式中,Ipre(t)為t時刻地表光照強度預測值,Istd(t)為t時刻標準晴天理論值,e(t)為預測計算用誤差百分數。
更進一步,步驟4的實現包括:
採用間接預測法,得到光照強度的預測數值後,通過光電轉換模型計算光伏輸出功率,計算公式為:
P=ηSI[1-0.005(t0+25)] (10);
(10)式中,η是光電轉換效率,S是用於光伏發電的有效總面積,I(t)是接收到的有效光照強度,t0為光伏電池的工作溫度。
實施例1
為了提高非晴天情況下的預測精度,提出一種基於Adaboost聚類和馬爾科夫鏈的分布式光伏超短期預測方法,採用滑動平均法提取光照強度序列的確定性分量,統計分析得到不同天氣類型的光照強度衰減因子;採用Adaboost改進的KNN方法對歷史數據的聚類分析,建立分類模型;結合基於誤差序列的多階加權馬爾科夫鏈實現未來時刻地表光照強度的預測,最後通過光電轉換模型實現分布式光伏發電超短期預測。
實施例1通過以下技術方案得以解決:
一種基於Adaboost聚類和馬爾科夫鏈的分布式光伏超短期預測方法,包括以下步驟:
S1,採用滑動平均法提取光照強度序列的確定性分量,統計分析得到不同天氣類型的光照強度衰減因子;
S2,採用Adaboost改進的KNN方法對歷史數據的聚類分析,建立分類模型;
S3,採用多階加權馬爾科夫鏈方法預測地表太陽輻照度;
S4,建立光電轉換模型,完成光伏功率超短期預測。
所述步驟S1中採用滑動平均法提取光照強度序列的確定性分量,統計分析得到不同天氣類型的光照強度衰減因子的流程如下:
選擇滑動平均法濾除光照強度的隨機波動分量,提取確定性分量並選擇該分量作為聚類分析的特徵變量。設原始光照強度實測值為yt,選擇滑動平均時間窗口m,平滑處理後的滑動平均值為Yt。
地表光照強度在雲層遮擋時刻有不同程度的下降,第i時刻地表光照強度Imea(i)與Hottel標準晴天理論值Istd(i)之間存在不同的倍率關係,記為衰減因子m。其表達式如下所示:
不同天氣類型下,地表輻照度較地外輻照度的衰減程度不一樣。
所述步驟S2採用Adaboost改進的KNN方法對歷史數據的聚類分析的預測流程為:
1)批量輸入訓練數據,提取數據的數學特徵,根據KNN確定弱分類器Gm(x)
的個數;
2)確定Adaboost學習過程中的迭代次數k,初始化各樣本數據的權重dmi。
3)根據權重選擇樣本點,得到新的訓練子集,用具有權值分布的訓練數據訓練弱分類器Gm(x),用Gm(x)對所有樣本進行分類,計算該弱分類器Gm(x)在訓練集下的誤差率em及其在最終分類器中的係數αm。
4)提高被正確分類的樣本權重,降低被錯誤分類的樣本權重,為下一輪迭代更新數據樣本的權重分布:
得到下一輪權重後返回步驟(3)進行下一輪迭代,直到迭代次數達到設置值或誤差率達到某個設定的足夠小的值。
所述步驟S3採用多階加權馬爾科夫鏈方法預測地表太陽輻照度流程如下:
I、對歷史數據預處理,獲得誤差百分數序列,定義相對預測誤差eit為:
其中為光照強度預測值;及為光照強度實際值;i為每日的預測點數;N為樣本數。
II、將預處理中得到的誤差百分數按實際運行經驗劃分為11個離散狀態,其中誤差小於-5%的點定義為狀態1,相鄰兩狀態的誤差級差為10%,依次類推,誤差大於85%的點定義為狀態11。
III、利用上述狀態劃分的結果,統計出各個步長(階數k不同)狀態變化的轉移頻數矩陣:
在m時刻太陽輻射的狀態為Si轉移到m+k時刻太陽輻射的狀態為Sj的的轉移概率為:
IV、誤差序列k階自相關係數計算公式如下:
其中xi表示第i時段的誤差,為平均誤差,n為時間長度。由求得的各階自相關係數計算各階影響權重:
V、得到的不同步長的狀態轉移概率矩陣後,由預測日某時段誤差百分數所在狀態預測出下一採樣時刻誤差百分數所在某一狀態的概率,並取得概率最大的一個狀態為預測誤差狀態,從而得到對應的預測誤差值,由下式完成當前時刻的預測:
Ipre(t)=Istd(t)×(1-e(t)) (23)
其中,Ipre(t)為t時刻地表光照強度預測值,Istd(t)為t時刻標準晴天理論值,e(t)為預測計算用誤差百分數。
所述S4建立光電轉換模型流程如下:
採用間接預測法,得到光照強度的預測數值後,通過光電轉換模型計算光伏輸出功率,計算公式如下所示:
P=ηSI[1-0.005(t0+25)] (24)
其中,η是光電轉換效率(%),S是用於光伏發電的有效總面積(m2),
I(t)是接收到的有效光照強度(kW/m2),t0為光伏電池的工作溫度(℃)。
實施例2
一種基於Adaboost聚類和馬爾科夫鏈的分布式光伏超短期預測方法,如圖1所示,包括以下步驟:
①採用滑動平均法提取光照強度序列的確定性分量,統計分析得到不同天氣類型的光照強度衰減因子。
在實施例2中,為提取光照強度序列的確定性分量,反映光照強度平均變化趨勢,選擇30min的時間窗口進行平滑處理,以實際數據為例,其處理效果如圖2所示。統計2015年~2016年歷史記錄數據與對應標準晴天模型數據,得到四種典型天氣類型下(晴天、多雲、雨天、陰天)衰減值的頻率分布如圖3所示,分布區間分別為[0,0.3)、[0.3,0.6)、[0.6,0.8)、[0.8,1]。各典型天氣類型下的衰減係數計算結果如表1所示。
表1典型天氣類型的衰減係數
②採用Adaboost改進的KNN方法對歷史數據的聚類分析,建立分類模型。
在實施例2中,結合武漢某光伏實驗平臺氣象監測設備2015年10月-2016年3月(實際有效數據量為130天)實時採樣間隔為5min的光照強度數據及溫度數據,將提取的光照強度序列確定性分量作為聚類程序的特徵輸入量,得到聚類中心如圖4所示;由KNN和Adaboost程序完成分類,迭代次數為7次,結合網絡氣象記錄得到的歷史天氣信息檢驗歷史數據分類的準確性,結果如下表所示:
表2天氣分類結果
③採用多階加權馬爾科夫鏈方法預測地表太陽輻照度。
(一)、對歷史數據預處理,獲得誤差百分數序列;
研究對象為標準晴天模型與實際值之間的差值,典型日光照強度曲線圖如圖5所示,圖中顯示差值狀態主要包括平穩區、波動區和驟變區,計算得到研究時段內平穩區差值總體分布在10%之內,波動區差值達到30%~40%,驟變區差值由於雲的遮擋有時甚至超過70%。
(二)、狀態劃分,計算狀態轉移概率矩陣;
將預處理中得到的誤差百分數按實際運行經驗劃分為11個離散狀態,其中誤差小於-5%的點定義為狀態1,相鄰兩狀態的誤差級差為10%,依次類推,誤差大於85%的點定義為狀態11,區間劃分如下表所示:
表3隨機狀態區間
統計出各個步長(階數k不同)狀態變化的轉移頻數矩陣,可計算各階11×11的轉移概率矩陣:
(三)、預測地表光照強度;
在步驟1和步驟2的基礎上,歷史數據被劃分為晴天、多雲、雨天和陰天四大類分別進行預測,本實施例選擇對預測日9:00至15:00時段的光照強度進行間隔5min的滾動預測,這裡選取平均絕對百分比誤差對預測效果進行評價:
其中,x為實測值;為預測值;P為光伏裝機容量。
歷史數據按照圖2方法被劃分為晴天、多雲、雨天和陰天作為相似日訓練樣本集,統計確定晴天光照強度衰減因子為0.83,輸入晴天預測子模型,預測結果如圖6所示;多雲光照強度衰減因子為0.69,輸入多雲預測子模型,預測結果如圖7所示;雨天光照強度衰減因子為0.35,輸入雨天預測子模型,預測結果如圖8所示;陰天光照強度衰減因子為0.12,輸入陰天預測子模型,預測結果如圖9所示。其平均絕對百分比預測誤差對比如下表所示:
表4不同模型預測誤差MAPE比較值
實施例2中採用某光伏實驗平臺某典型日前3個月的數據為基礎時間序列,對典型日6小時的地表光照強度進行預測。預測結果顯示本發明所提聚類組合預測模型預測效果整體優於傳統馬爾科夫鏈預測模型。對於大幅度高頻率震蕩的多雲類天氣及光照強度大幅下降的陰雨天氣,傳統馬爾科夫鏈模型預測誤差有所降低,很難有規律的跟蹤光照強度幅值的快速變化,且陰天變化的細節不能得到很好的分析,引入衰減係數m後預測模型對光照強度的跌落反應更準確,減少了峰值、谷值的錯誤預報,提高了在晴天情況和非晴天情況下的預測精度。
④建立光電轉換模型,完成光伏功率超短期預測。
實施例2中實驗平臺採用英利YL175P-23b型多晶矽電池板,轉換效率為15%,得到光照強度的預測數值後,通過光電轉換模型計算光伏輸出功率,計算公式如下所示:
P=ηSI[1-0.005(t0+25)] (27)
其中,η是光電轉換效率(%),S是用於光伏發電的有效總面積(m2),I(t)是接收到的有效光照強度(kW/m2),t0為光伏電池的工作溫度(℃)。
應當理解的是,本說明書未詳細闡述的部分均屬於現有技術。
雖然以上結合附圖描述了本發明的具體實施方式,但是本領域普通技術人員應當理解,這些僅是舉例說明,可以對這些實施方式做出多種變形或修改,而不背離本發明的原理和實質。本發明的範圍僅由所附權利要求書限定。
