一種都卜勒效應消除方法與流程
2023-05-22 14:52:06 2
本發明涉及物理專業中噪聲類領域都卜勒效應消除方法,更具體地說是在時域—波數域消除都卜勒效應的一種方法。
背景技術:
噪聲分析是機械零部件狀態監測和故障診斷的一個重要方法。但當機械零部件處於移動狀態時,其診斷的有效性將大大降低,主要原因就是機械零部件與傳聲器之間的相對運動引起的都卜勒效應。都卜勒效應會對採集到的聲信號造成幅值畸變和頻率偏移,這會對診斷效果造成嚴重影響。因此如何準確地消除都卜勒效應對移動機械零部件的診斷有重要意義。目前消除都卜勒效應的方法主要有頻域方法和時域方法。頻域方法能夠準確地消除都卜勒效應,但通常只能對穩態信號進行計算。時域方法直接在時域進行計算,不僅可以計算穩態信號,還可對非穩態信號進行計算。目前消除都卜勒效應的時域計算方法主要有重採樣方法,非線性時間映射方法以及基於完整morse聲學模型的去都卜勒效應方法。但這些方法在消除都卜勒效應時都有一些缺陷,比如重採樣方法需要對信號進行插值擬合計算,計算效率較低,非線性時間映射方法和基於完整morse聲學模型的去都卜勒效應方法需要聲源的初始位置信息,使其在實際應用中受到限制。
技術實現要素:
本發明為彌補重採樣方法的計算效率低以及非線性時間映射方法和基於完整morse聲學模型的去都卜勒效應方法需要聲源初始位置信息的不足,提供一種高效、無需聲源初始位置的都卜勒效應消除方法。
本發明為解決技術問題採用的技術方案是:
本發明都卜勒效應消除方法的特點是按如下步驟進行:
步驟1、在空間中建立兩個坐標系,一個是靜止的固定坐標系of(xf,yf,zf),另一個是隨聲源以相同速度運動的移動坐標系om(xm,ym,zm);兩個坐標系原點在t=0時刻位於同一位置;在空間中放置一聲源,聲源在xfofyf平面內做直線移動;在移動聲源輻射聲場中設置固定坐標系下的測量面,在測量面上等間隔均勻分布n個測量點;n個測量點中第n個測量點在固定坐標系下坐標為第n個測量點在移動坐標系下坐標為第n個測量點在兩個坐標系下坐標的相對關係為:
其中vx表示聲源移動速度在xf軸正方向上的分量,vy表示聲源移動速度在yf軸正方向上的分量;
步驟2、將n個傳聲器一一對應地放置在所述n個測量點處進行測量,獲得聲壓信號,包括:
在接收時刻t,各測量點處在固定坐標系下的聲壓信號一一對應為:
將所有n個測量點處的聲壓信號pf表徵為:
在接收時刻t,各測量點處在移動坐標系下的聲壓信號一一對應為:
將所有n個測量點在移動坐標系下聲壓信號pm表徵為:
在接收時刻t,各測量點處不含都卜勒效應的聲壓信號一一對應為:
將所有n個測量點不含都卜勒效應的聲壓信號pd表徵為:
步驟3、根據n個測量點在兩個坐標系下坐標的相對關係,將n個測量點在移動坐標系下的聲壓信號pm表徵為:
步驟4、根據測量點處聲壓信號在任一坐標系下不變的先驗條件pm=pf,計算獲得各測量點含有都卜勒效應的聲壓信號pf與不含都卜勒效應的聲壓信號pd在時域—波數域的相對關係表徵為:f(pf)=exp(-jkxvxt)×exp(-jkyvyt)×f(pd),其中,f表示空間傅立葉變換運算,exp表示指數運算,kx表示在xf方向上的波數劃分,ky表示在yf方向上的波數劃分,j表示虛數單位;
步驟5、根據各測量點測得的含有都卜勒效應的聲壓信號pf,結合數值傅立葉變換運算,計算獲得各測量點不含都卜勒效應的聲壓信號表徵為:
pd=f-1[exp(jkxvxt)×exp(jkyvyt)×f(pf)],
其中f-1表示空間逆傅立葉變換運算,從而實現都卜勒效應的消除。
本發明都卜勒效應消除方法的特點也在於:所述n個測量點是在平面上等間隔均勻分布。
本發明都卜勒效應消除方法的特點也在於:聲源移動速度為固定值或隨時間變化。
本發明都卜勒效應消除方法的特點也在於:所述聲源為一個或多個,聲源信號為穩態信號或非穩態信號。
本發明都卜勒效應消除方法的特點也在於:所述空間坐標係為三維坐標系或二維坐標系。
與已有技術相比,本發明有益效果體現在:
1、本發明方法無需插值擬合計算,計算效率較高;
2、本發明方法無需聲源初始位置的先驗信息,能夠準確消除未知初始位置聲源的都卜勒效應。
附圖說明
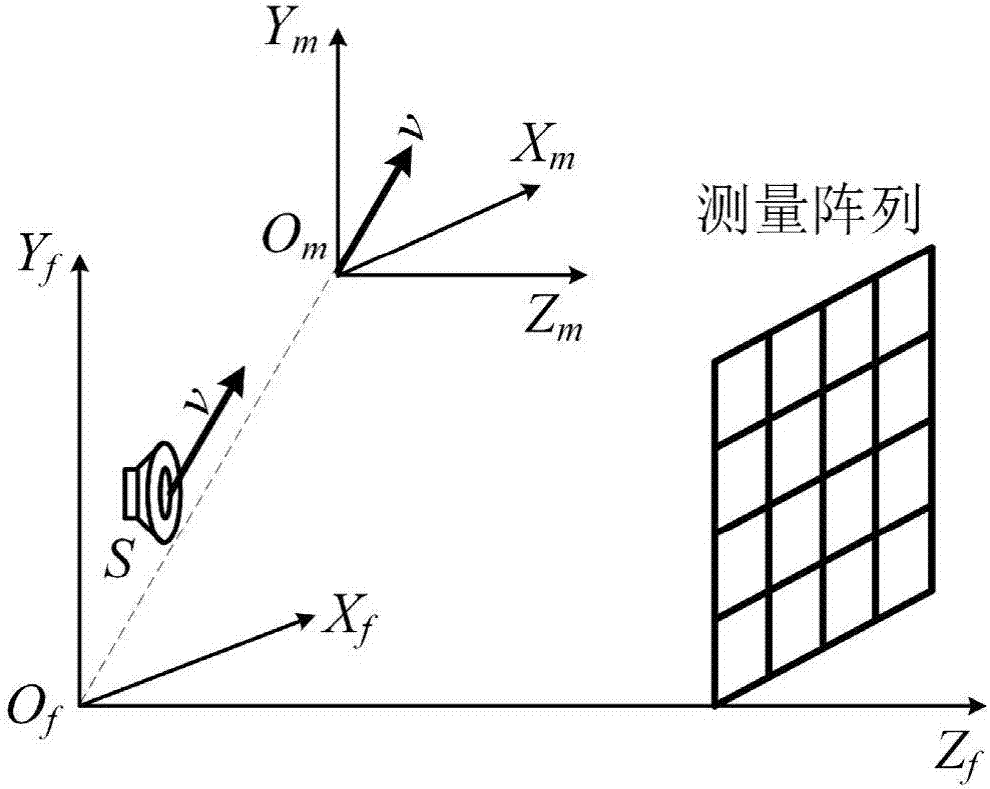
圖1為本發明方法中固定坐標系、移動坐標系、聲源s及測量點位置示意圖;
圖2a為在聲源移動時測量點a接收時域信號與利用本發明方法消除都卜勒效應後的時域信號的對比,圖2a中以點表徵的曲線為實際測量得到的時域信號,以實線表徵的曲線為採用本發明方法消除都卜勒效應後的時域信號;
圖2b為在聲源移動時測量點a接收信號的頻譜與利用本發明方法消除都卜勒效應後的信號頻譜的對比,圖2b中以點表徵的曲線為實際測量得到的信號頻譜,以實線表徵的曲線為採用本發明方法消除都卜勒效應後的信號頻譜;
圖2c為在聲源移動時測量點b接收時域信號與利用本發明方法消除都卜勒效應後的時域信號的對比,圖2c中以點表徵的曲線為實際測量得到的時域信號,以實線表徵的曲線為採用本發明方法消除都卜勒效應後的時域信號;
圖2d為在聲源移動時測量點b接收信號的頻譜與利用本發明方法消除都卜勒效應後的信號頻譜的對比,圖2d中以點表徵的曲線為實際測量得到的信號頻譜,以實線表徵的曲線為採用本發明方法消除都卜勒效應後的信號頻譜。
具體實施方式
本實施例中都卜勒效應消除方法是按如下步驟進行:
步驟1、如圖1所示,在空間中建立兩個坐標系,一個是靜止的固定坐標系of(xf,yf,zf),以f表示固定坐標系,另一個是隨聲源以相同速度運動的移動坐標系om(xm,ym,zm),以m表示移動坐標系;兩個坐標系原點在t=0時刻位於同一位置;在空間中放置一聲源,聲源在xfofyf平面內做直線移動,具體實施中,聲源s以速度v做勻速直線移動;在移動聲源輻射聲場中設置固定坐標系下的測量面,在測量面上等間隔均勻分布n個測量點,具體實施中,測量點組成一個平面陣列,並與xfofyf平面平行;n個測量點中第n個測量點在固定坐標系下坐標為第n個測量點在移動坐標系下坐標為第n個測量點在兩個坐標系下坐標的相對關係為:
其中vx表示聲源移動速度在xf軸正方向上的分量,vy表示聲源移動速度在yf軸正方向上的分量。
步驟2、將n個傳聲器一一對應地放置在n個測量點處進行測量,獲得聲壓信號,包括:
在接收時刻t,各測量點處在固定坐標系下的聲壓信號一一對應為:
將所有n個測量點處的聲壓信號pf表徵為:
在接收時刻t,各測量點處在移動坐標系下的聲壓信號一一對應為:
將所有n個測量點在移動坐標系下聲壓信號pm表徵為:
在接收時刻t,各測量點處不含都卜勒效應的聲壓信號一一對應為:
將所有n個測量點不含都卜勒效應的聲壓信號pd表徵為:以d表示消除都卜勒效應後的信號。
步驟3、根據n個測量點在兩個坐標系下坐標的相對關係,將n個測量點在移動坐標系下的聲壓信號pm表徵為:
步驟4、根據測量點處聲壓信號在任一坐標系下不變的先驗條件pm=pf,計算獲得各測量點含有都卜勒效應的聲壓信號pf與不含都卜勒效應的聲壓信號pd在時域—波數域的相對關係表徵為:f(pf)=exp(-jkxvxt)×exp(-jkyvyt)×f(pd),其中,f表示空間傅立葉變換運算,具體實施中:
exp表示指數運算,kx表示在xf方向上的波數劃分,ky表示在yf方向上的波數劃分,j表示虛數單位。
步驟5、根據各測量點測得的含有都卜勒效應的聲壓信號pf,結合數值傅立葉變換運算,計算獲得各測量點不含都卜勒效應的聲壓信號表徵為:
pd=f-1[exp(jkxvxt)×exp(jkyvyt)×f(pf)],
其中f-1表示空間逆傅立葉變換運算,具體實施中:
π為圓周率,從而實現都卜勒效應的消除。
為了進行空間傅立葉變換運算,n個測量點是在平面上等間隔均勻分布,聲源移動速度為固定值或隨時間變化,聲源為一個或多個,聲源信號為穩態信號或非穩態信號,空間坐標係為三維坐標系或二維坐標系。
具體實施中,聲源s採用一個單極子,在固定坐標系of(xf,yf,zf)中位於(0.5m,0.5m,0m),聲源移動速度v在xf軸正方向上的分量為vx=60m/s,在yf軸正方向上的分量為vy=60m/s。測量陣列位於zf=0.2m的平面上,陣列包含121×121個等間隔均勻分布的測量點,相鄰兩個測量點之間距離為0.05m。聲源s輻射三個頻率組合的正弦信號,其表達式為:
s(t)=sin(2πf1t)+sin(2πf2t)+sin(2πf3t)(1)
在式(1)中,頻率f1=960hz,f2=1000hz,f3=1040hz。時域信號採樣頻率為10.24khz,採樣點數為512。
為檢驗本發明方法消除都卜勒效應的效果,選取了兩個測量點,即測量點a和測量點b,其位置分別為a(0.5m,0.5m,0.2m)、b(1m,1m,0.2m)。圖2a和圖2c分別表示測量點a和測量點b接收時域信號與利用本發明方法消除都卜勒效應後的時域信號的對比,圖中以點表徵的曲線為實際測量得到的時域信號,以實線表徵的曲線為採用本發明方法消除都卜勒效應後的時域信號;圖2b和圖2d分別表示測量點a和測量點b接收信號的頻譜與利用本發明方法消除都卜勒效應後的信號頻譜的對比,圖中以點表徵的曲線為實際測量得到的信號頻譜,以實線表徵的曲線為採用本發明方法消除都卜勒效應後的信號頻譜。比較圖中的實線和點線可以看出,採用本發明方法可以很好地修正都卜勒效應帶來的幅值畸變和頻率偏移,消除測量信號中的都卜勒效應。
