基於動態閾值確定嵌入維的神經網絡時間序列預測方法與流程
2023-05-14 09:31:26 1
本發明涉及神經網絡信號處理領域,具體涉及基於動態閾值確定嵌入維的神經網絡時間序列預測方法。
背景技術:
時間序列的混沌特性在金融、農業、天氣以及太陽黑子的活動中普遍存在,對這些領域的時間序列進行預測有著積極的現實意義。
我們知道,對於大多數時間序列而言,數據的大小通常不只是由單個變量所決定的。例如某隻股票每天的收盤價格,在繪製的圖像上是關於時間而變化的變量,但該價格往往是由公司的經營狀況、市場的整體環境、股民的投資心態等各種因素所決定的。所以,對於特定的時間序列,可看成是多變量系統。決定多變量系統長期深化的任一變量的時間演化,均包含了系統長期演化的信息。因此,可以通過對決定系統演化的任一單變量時間序列的分析來研究系統的混沌行為。通過時間序列對混沌進行研究,開始於packard等人提出的相空間重構理論。而在相空間重構中,對於時間延遲和嵌入維數的選擇具有十分重要的意義。
與此同時,利用神經網絡對混沌時間序列進行預測,已經成為了當前的熱點研究課題。對混沌時間序列嵌入維的計算,決定著神經網絡的結構,從而深刻影響著神經網絡對混沌時間序列預測的精確度。當前對混沌時間序列嵌入維的計算方法有:奇異值分解法、假鄰近法等。奇異值分解法,首先對嵌入空間進行奇異值分解,然後選取最大奇異值作為最小嵌入空間的維數。假鄰近法,根據在嵌入維小於吸引子真實維數的時候,會出現很多假鄰近點,即在低維的情況下某點是鄰近點,但隨著嵌入維的增加,該點已經不是鄰近點了。由此定義了兩點是否是鄰近點的判定準則,再根據鄰近點數目是否為0來判定嵌入維數。這些方法對數據初始值敏感,且對於閾值沒有一種明確的設定方法,只根據經驗來決定閾值,因此無法保證嵌入維計算結果的準確性,進而影響神經網絡的健壯性,導致預測結果誤差較大。
技術實現要素:
為了克服現有技術存在的缺點與不足,本發明提供一種基於動態閾值確定嵌入維的神經網絡時間序列預測方法。通過動態閾值的引入,得到更加準確的嵌入維數值,將混沌動力學系統與神經網絡結合起來,根據嵌入維和時間延遲構造更健壯合理的神經網絡結構,同時結合構造的訓練數據集,得到更好的訓練及預測效果。
本發明採用如下技術方案:
一種基於動態閾值確定嵌入維的神經網絡時間序列預測方法,包括如下步驟:
s1判定時間序列的混沌特性,得到混沌時間序列;
s2對混沌時間序列進行數據歸一化處理;
s3利用自相關函數法計算混沌時間序列的時間延遲;
s4利用動態閾值方法計算混沌時間序列的嵌入維;
s5利用時間延遲和嵌入維構造bp神經網絡的輸入層結構;
s6利用時間延遲和嵌入維構造bp神經網絡的訓練數據集;
s7利用構造的bp神經網絡對混沌時間序列數據組進行訓練及預測。
所述s3中利用自相關函數法計算混沌時間序列的時間延遲,具體為:
對於一個混沌時間序列,寫出其自相關函數,然後作出自相關函數關於時間t的函數圖像,根據函數的數值分析,當自相關函數下降到初始值的1-1/e時,所得的時間t為重構相空間的時間延遲t。
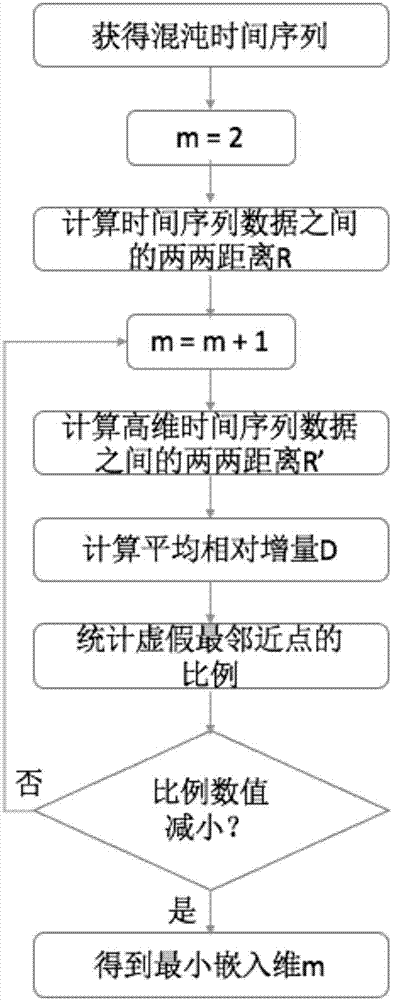
所述s4利用動態閾值方法計算混沌時間序列的嵌入維,具體步驟如下:
s4.1混沌時間序列x(n)和延遲時間t,構造一個m維的狀態空間矢量y(n),用第r個鄰近點xr表示的,他們之間的距離定義為r,m為整數;
s4.2當狀態空間維數從m增加到m+1時,y』(n)上分別增加一個新的坐標分量為x(n+mt)和x』(n+mt),這時y(n)和y』(n)之間的距離為距離的相對增量為
s4.3引入循環計數器和平均相對增量d,其中d為嵌入維m每增加一維之後相對增量的平均值,當嵌入空間的維數從m增加到m+n時,此時若相對增量r大於d,則認為該點為假最鄰近點;
s4.4作出假最鄰近點數目和嵌入維的函數圖像,隨著嵌入維數值的增加,假最鄰近點的數目會逐漸減少,直至減少至0或不再變化,當假最鄰近點的數目趨近於0或不再變化時,終止計算,此時嵌入維的數值作為該序列的最小嵌入維;否則循環s4.1~s4.3。
所述m大於等於2。
所述s5中構造的bp神經網絡為三層,包括一個輸入層,一個隱含層及一個輸出層。
s7利用構造的bp神經網絡對混沌時間序列數據組進行訓練及預測,具體步驟為:
s7.1根據連接權矩陣和訓練樣本數據集計算隱含層新的激活值
使用的激活函數為sigmoid函數f(x)=1/(1+e-x);
s7.2計算輸出層單元的激活值
s7.3計算輸出層單元的一般化誤差;
s7.4計算隱含層單元相對於每個神經元的誤差;
s7.5調整隱含層到輸出層單元的連接權值;
s7.6調整輸出層單元的閾值;
s7.7調整輸入層單元到隱含層單元的連接權值;
s7.8調整隱含層單元的閾值;
重複第s7.1至s7.8的計算步驟,當全部樣本的輸出誤差小於設定的收斂誤差時,訓練結束,運用已經構建好的bp神經網絡,對時間序列進行預測;
w為神經網絡中神經元的權值參數,b為神經網絡中神經元的偏置參數,f為激活函數。
本發明的有益效果:
(1)靈活性:本發明根據特定混沌時間序列數據的特點,靈活地利用動態閾值的方法計算嵌入維,替代了以往一味根據經驗確定閾值的思想,有著良好的自適應能力;
(2)健壯合理性:本發明根據時間延遲和嵌入維,合理地構造bp神經網絡的訓練數據集,同時確定了bp神經網絡輸入層的神經元個數,增強了神經網絡結構的健壯性,這兩方面都提高了神經網絡的預測準確度。
(3)魯棒性:本發明所採用的基於動態閾值計算嵌入維的方法,針對不同的混沌時間序列能夠確定不同的閾值,有著良好的推廣性,魯棒性強。
附圖說明
圖1是本發明的工作流程圖;
圖2是本發明利用動態閾值計算最小嵌入維的流程圖;
圖3是最小嵌入維與構造神經網絡之間的關係圖;
圖4是本發明實施例汽車數據序列歸一化的圖;
圖5是本發明實施例中通過matlab得到嵌入維m的比例變化情況圖;
圖6是本實施例預測的結果與真實值比較圖。
具體實施方式
下面結合實施例及附圖,對本發明作進一步地詳細說明,但本發明的實施方式不限於此。
實施例
如圖1-圖2所示,一種基於動態閾值確定嵌入維的神經網絡時間序列預測方法,包括如下步驟:
s1判定時間序列的混沌特性,得到混沌時間序列;
通過計算時間序列的lyapunov指數,可以判斷序列的混沌特性。一個正的lyapunov指數,意味著在系統相空間中,無論初始兩條軌線的間距多麼小,其差別都會隨著時間的演化而成指數率的增加以致達到無法預測,這就是混沌現象。指數越大,說明混沌特性越明顯,混沌程度越高。
s2對混沌時間序列進行數據歸一化處理;
若輸入神經網絡的數據單位不一樣,有些數據的範圍可能特別大,會導致神經網絡收斂慢、訓練時間長;另外,由於神經網絡輸出層的激活函數的值域是有限制的,因此需要將網絡訓練的目標數據映射到激活函數的值域中。
本發明採用的歸一化方法為線性轉換方法——最大最小值法:
y=(x-min)/(max-min)
其中min為x的最小值,max為x的最大值,輸入向量為x,歸一化後的輸出向量為y。上式將數據歸一化到[0,1]區間,當激活函數採用sigmoid函數時(值域為(0,1))時這種方法適用。
s3利用自相關函數法計算混沌時間序列的時間延遲;
對於一個混沌時間序列,寫出其自相關函數,然後作出自相關函數關於時間t的函數圖像,根據函數的數值分析,當自相關函數下降到初始值的1-1/e時,所得的時間t為重構相空間的時間延遲t。e是自然對數函數的底數,約為2.71828。
s4利用動態閾值方法計算混沌時間序列的嵌入維,具體為:
s4.1混沌時間序列x(n)和延遲時間t,構造一個m維的狀態空間矢量y(n),用表示的第r個鄰近點xr,它們之間的距離定義為r,m為整數;
s4.2當狀態空間維數從m增加到m+1時,y』(n)上分別增加一個新的坐標分量為x(n+mt)和x』(n+mt),這時y(n)和y』(n)之間的距離為距離的相對增量為
s4.3引入循環計數器和平均相對增量d,其中d為嵌入維m每增加一維之後相對增量的平均值,當嵌入空間的維數從m增加到m+n時,此時若相對增量r大於d,則認為該點為假最鄰近點;
s4.4作出假最鄰近點數目和嵌入維的函數圖像,隨著嵌入維數值的增加,假最鄰近點的數目會逐漸減少,直至減少至0或不再變化,當假最鄰近點的數目趨近於0或不再變化時,終止計算,此時嵌入維的數值作為該序列的最小嵌入維;否則循環s4.1~s4.3。
本步驟的主要思想為:在m維的空間中,對於任何一個矢量,都有一個歐幾裡德的最鄰近矢量,兩個矢量之間的距離可以定義為r。而當相空間的維數從m維增加到m+1維時,距離r也會發生變化。從嵌入維m的最小值2開始,計算虛假鄰近點在所有點中的比例,當比例為0或不再隨著m的增加而減小時,說明此時m為最佳嵌入維,此時重構出來的系統最能體現原時間序列。以往總是根據相對距離r大於經驗值10時,判定兩個矢量是不相鄰的。
如圖3所示,s5利用時間延遲和嵌入維構造bp神經網絡的輸入層結構;
通過時間序列已有的m個數值,來預測未來時間序列的1個數值,這裡的m對應了bp神經網絡輸入層神經元的個數。嵌入維數值等於m-1,時間延遲則決定了m個數據之間間隔的大小。例如,若嵌入維等於5,時間間隔為2,則輸入層神經元的個數即為(5-1)=4,輸入層為x1、x3、x5、x7,預測值為x9。
所述s5中構造的bp神經網絡為三層,包括一個輸入層,一個隱含層及一個輸出層,輸入層神經元的個數為m-1,輸出層神經元個數為1,所述m大於等於2。
s6利用時間延遲和嵌入維構造bp神經網絡的訓練數據集;
s7利用構造的bp神經網絡對混沌時間序列數據組進行訓練及預測。這裡的混沌時間序列即s1中的時間序列。
本方法所構造的神經網絡結構為3層bp神經網絡,該網絡包括一個輸入層、一個隱含層和一個輸出層,輸入層至隱含層、隱含層至輸出層的連接權值都是隨機生成的,輸出樣本及輸出樣本為前面步驟中運用時間延遲和嵌入維所構造的訓練數據集。訓練的步驟如下:
s7.1根據連接權矩陣和訓練樣本數據集計算隱含層新的激活值
使用的激活函數為sigmoid函數f(x)=1/(1+e-x);
s7.2計算輸出層單元的激活值
s7.3計算輸出層單元的一般化誤差;
s7.4計算隱含層單元相對於每個神經元的誤差;
s7.5調整隱含層到輸出層單元的連接權值;
s7.6調整輸出層單元的閾值;
s7.7調整輸入層單元到隱含層單元的連接權值;
s7.8調整隱含層單元的閾值;
重複第s7.1至s7.8的計算步驟,當全部樣本的輸出誤差小於設定的收斂誤差時,訓練結束,運用已經構建好的bp神經網絡,對時間序列進行預測。
參數的物理意義:w為神經網絡中神經元的權值參數,b為神經網絡中神經元的偏置參數,f為激活函數。
本方法自適應地對時間序列的嵌入維進行計算,取代以往通過經驗值來計算嵌入維,利用嵌入維進行數據分組的思想來構造神經網絡訓練集,將混沌動力學系統與神經網絡結合起來,從而使神經網絡的預測能力更加準確。
本方法可以應用需要預測的很多領域,本實施例中將本方法應用在預測每月汽車銷量上。
選用的是魁北克(加拿大東部重要城市及港口)1960年至1968年每月汽車銷量的時間序列(總共108個月)。
具體如下:
s1判定時間序列的混沌特性,得到混沌時間序列;
s2對混沌時間序列進行數據歸一化處理;
對魁北克1960年至1968年每月汽車銷量的時間序列(總共108個月)進行歸一化並作圖4所示,
s3利用自相關函數法計算混沌時間序列的時間延遲;
利用自相關函數法計算混沌時間序列的時間延遲。對於一個混沌時間序列,先寫出其自相關函數,然後作出自相關函數關於時間t的函數圖像。根據函數的數值分析,當自相關函數下降到初始值的1-1/e時,所得的時間t重構相空間的時間延遲t。在這裡,計算得到魁北克汽車銷量時間序列的時間延遲t為8。
s4利用動態閾值方法計算混沌時間序列的嵌入維,得到在魁北克每月汽車銷量的時間序列中,我們通過matlab得到嵌入維m的比例變化情況,如圖5所示。
魁北克每月汽車銷量時間序列的嵌入維m為4。
s5利用時間延遲和嵌入維構造bp神經網絡的輸入層結構;
在構造bp神經網絡的輸入層及輸出層時,輸入層神經元的個數為m–1即3,輸出層神經元個數為1。
s6利用時間延遲和嵌入維構造bp神經網絡的訓練數據集
具體過程如下:根據上述步驟得到了汽車銷量時間序列的延遲時間和嵌入維,混沌時間序列為xi={x1,x2,…,x10},時間延遲t=8,嵌入維m=4,得到訓練數據集為x1=[x1,x9,x17,x25]t,x2=[x2,x10,x18,x26]t,x3=[x3,x11,x19,x27],x4=[x4,x12,x20,x28],……。根據s5所述,每組訓練數據集的前3個分量作為輸入,後一分量作為輸出的驗證值。
s7在這裡,對數據進行分成訓練、驗證以及測試3組,比例分布為:訓練數據佔整個數據集的70%;驗證數據佔整個數據集的15%;預測數據佔整個數據集的15%。
我們將預測的結果與真實值進行比較,如圖6所示,可見誤差都在一個比較小的範圍之內。在圖6中,橫坐標為汽車銷量108個月的數據坐標值,如橫坐標為8,則對應數據x8:
上述實施例為本發明較佳的實施方式,但本發明的實施方式並不受所述實施例的限制,其他的任何未背離本發明的精神實質與原理下所作的改變、修飾、替代、組合、簡化,均應為等效的置換方式,都包含在本發明的保護範圍之內。
