一種基於多參數區間數多屬性決策的雲服務信任評估方法與流程
2023-05-14 13:18:16 1
本發明涉及雲計算領域,具體是一種基於多參數區間數多屬性決策的雲服務信任評估方法。
背景技術:
隨著網絡、巨型計算和大數據的發展,商用為主的雲計算得到大力推廣,越來越多的企業推出雲服務。面對眾多功能相同或相近,而質量不同的雲服務,如何對其進行客觀的信任評估,為用戶提供個性化推薦已成為當前雲計算領域亟待解決的問題。傳統的雲服務信任評估方法存在很多不足:套用現成的web服務評價模型,無法適應新需求;缺乏定量的從多個方面對雲服務質量度量的方法,評價不夠準確;評價體系局限於雲服務某幾個指標,擴展困難;採用確定的QoS值進行信任評估,缺乏對雲服務指標範圍的限定;指標權重的設定中加入過多的主觀評價因素,雲服務的信任評估缺乏客觀性等。
技術實現要素:
針對上述問題,本發明提出一種基於多參數區間數多屬性決策的雲服務信任評估方法,與現有方法相比具有更強的客觀性和實用性。
實現本發明目的的技術方案是:
一種基於多參數區間數多屬性決策的雲服務信任評估方法,包括如下步驟:
(1)基於多參數區間數的數據採集及處理,以多參數區間數形式採集雲服務運行的QoS指標數據並列出決策矩陣,將多參數區間數形式的指標值轉換成二元聯繫數,再按照成本型和效益型類型對決策矩陣規範化處理得到規範化決策矩陣;
(2)基於聯繫數的屬性權重未知的權重設定,依據「雲服務指標值波動越大的指標應該賦予越大的權重」的原則,確定QoS指標權重;
(3)進行雲服務信任評估,基於規範化決策矩陣和QoS指標權重,採用主值模型對雲服務信任評估。
步驟(1)所述基於多參數區間數的數據採集及處理,具體步驟如下:
(1-1)定義所研究的雲服務集為S={S1,S2,...,Si,...,Sn},每一個雲服務對應m個QoS指標,有Q={q1,q2,...,qm},各指標數據以多參數區間數形式表示;
(1-2)採集數據,通過監測雲環境,觀察不同雲服務的運行情況,以多參數區間數形式採集雲服務運行的QoS指標數據,列出決策矩陣。其中,多參數區間數是指區間數的參數為三個及以上,傳統的區間數決策問題一般採用由一個最大值和一個最小值兩個參數組成的區間數表示指標數據,這種選取方法缺乏代表性,本方法在傳統區間數基礎上增加了在2/4和3/4兩個百分點所監測到的數據,共同組成一個四參數的區間數,以qik表示雲服務Si的QoS指標qk的多參數區間數,則有:其中,表示在整個檢測過程中檢測到的最小值;表示在第2/4百分點檢測到的數據;表示在第3/4百分點檢測到的數據;表示檢測到的最大值;基於qik的雲服務QoS指標決策矩陣如下所示:
(1-3)將多參數區間數形式的指標值qik轉換成二元聯繫數,得到「均值+最大偏差」二元聯繫數uik,既保存了區間數對範圍的限定作用,又減少了區間數的不確定性,uik的計算公式如下:
其中,j∈[-1,1];
(1-4)將以複數形式的二元聯繫數uik轉化成等價的三角函數Uik,三角函數成為原區間數的一個代表點,令(cosθ+jsinθ)=1,用三角函數Uik的模rik表示三角函數Uik,則稱rik為三角形的主值,用三角函數的主值代替三角函數參與運算,在保證結果一致性的基礎上,大大簡化運算過程,具體公式表示如下:
(1-5)將步驟(1-4)中進行指標數據轉換後的決策矩陣中的QoS指標數據按照指標的效益型和成本型兩類進行規範化處理,效益型指標是指數值越大越好的指標,如資源利用率,可靠性,準確性等;成本型指標是指數值越小越好的指標,如響應時間,成本等。通過規範化處理,可以去除不同QoS指標的量綱,從而實現對不同指標的融合計算;並能夠將不同指標數據轉化為特定區間的數據,避免不同數據數值的巨大波動相互影響。對效益型指標和成本型指標的規範化處理方法是不同的,以r'ik表示規範化後的指標,具體規範化如下:
對效益型指標的規範化處理公式如下:
對成本型指標的規範化處理公式如下:
(1-6)基於對不同QoS指標規範處理後的規範化決策矩陣X'如下:
其中,q'ik=r'ik;i=1,2,...,n;k=1,2,...,m。
步驟(2)所述中基於聯繫數的屬性權重未知的權重設定,其原理為:如果所有雲服務在第k個指標Qk下的指標值波動較小,說明該指標對雲服務信任評估的影響越小;反之,指標Qk在各雲服務中的指標值波動較大,說明該指標對雲服務信任評估的影響越大。因此,從雲服務信任評估這一角度考慮,雲服務指標值波動越大的指標應該賦予越大的權重。特別地,當所有雲服務在指標Qk下的各屬性值沒有絲毫波動,則該指標Qk對雲服務信任評估將不起作用,可令其權重為零。基於步驟(1)求得的規範後的決策矩陣X',指標的權重計算具體步驟如下:
(2-1)定義QoS指標的權重向量集為W=(ω1,ω2,...,ωi,...,ωm),並滿足歸一化約束m為指標數量;
(2-2)為了表達指標值的波動性,計算n個雲服務中k個指標值的模的方差,公式如下:
式中,是規範化決策矩陣中雲服務各QoS指標模的平均數;
(2-3)把m個Qk值歸一化處理,計算得到各指標權重ωk,,公式如下:
基於公式(8)求得QoS指標的權重向量集為W=(ω1,ω2,...,ωi,...,ωm),並滿足歸一化約束
步驟(3)所述進行雲服務信任評估,基於所求得規範化決策矩陣和QoS指標權重體系,採用線性加權方法實現對雲服務的信任評估,具體步驟如下:
(3-1)將步驟(1)中所求的規範化決策矩陣X'與步驟(2)中所求得的指標權重向量集W,代入雲服務的信任評估線性加權公式中,計算雲服務的信任評估值,以T(Si)表示第i個雲服務Si的信任評估值,其計算公式如下:
T(Si)=∑(q'ik×wk),i=1,2,...,n;k=1,2,...,m (9)
其中,ωk為步驟(2)中所求得的指標權重集;q'ik為規範化決策矩陣X'中第i行k列的QoS指標數據;其中,規範化決策矩陣中QoS指標數據q'ik以三角函數主值的形式參與信任評估,這種評估模型稱之為主值模型。採用主值模型進行信任評估,將區間數轉換成二元聯繫數uik,接著,將uik轉化成三角函數,三角函數成為原區間數的一個代表點,用三角函數主值參與信任評估,保存了原區間數對範圍的限定,降低了不確定性,簡化了運算過程;
(3-2)依據步驟(3-1)中的雲服務的信任評估公式,計算各雲服務的信任評估值;進一步對同一雲提供商的不同服務或不同雲提供商的同一服務進行信任評估。
本發明的有益效果是,以多參數區間數形式採集QoS指標數據,在傳統區間數基礎上增加了在2/4和3/4兩個百分點所監測到的數據,共同組成一個四參數的區間數,保證了數據的真實性和客觀性;基於聯繫數的屬性權重未知的區間數多屬性決策方法確定QoS指標權重,使權重的確定依賴於採集的QoS指標數據的波動性,提高了決策的客觀性,避免了人為主觀因素的影響,其計算結果更加客觀、真實;依據主值模型計算雲服務的綜合評價值,將區間數化為聯繫數,減少了區間數的不確定性又簡化了計算過程,同時降低了評估方法的時間複雜度。因此,本發明方法具有更強的客觀性和實用性。
附圖說明
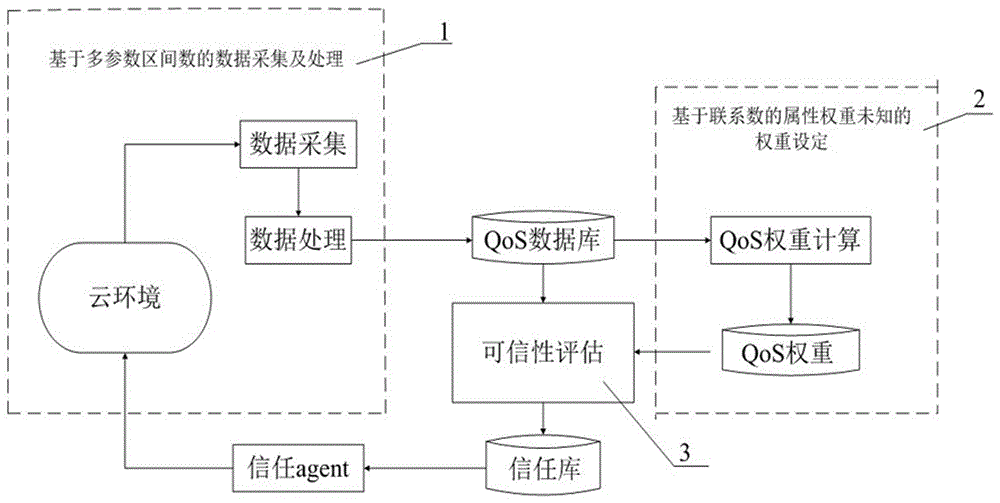
圖1為本發明的雲服務信任評估模型框架圖;
圖中,1、基於多參數區間數的數據採集及處理模塊,2、基於聯繫數的屬性權重未知的權重設定模塊,3、雲服務信任評估模塊。
具體實施方式
以下結合附圖對本發明內容做進一步闡述,但不是對本發明的限定。
如圖1所示,一種基於多參數區間數多屬性決策的雲服務信任評估方法,具體步驟如下:
(1)基於多參數區間數的數據採集及處理模塊1,通過監測雲環境中雲服務的運行狀況,以多參數區間數形式採集雲服務運行的QoS指標數據並列出決策矩陣,接著,進行數據處理得到QoS資料庫;
(2)基於聯繫數的屬性權重未知的權重設定模塊2,依據「雲服務指標值波動越大的指標應該賦予越大的權重」的原則,基於步驟(1)所求得的QoS資料庫,確定QoS指標權重;
(3)進行雲服務信任評估模塊3,基於步驟(1)所求得的QoS資料庫和步驟(2)所得的QoS指標權重,採用主值模型對雲服務進行可信性評估,得到信任庫。
步驟(1)所述基於多參數區間數的數據採集及處理模塊1,具體步驟如下:
(1-1)定義所研究的雲服務集為S={S1,S2,...,Si,...,Sn},每一個雲服務對應m個QoS指標,有Q={q1,q2,...,qm},各指標數據以多參數區間數形式表示;
(1-2)採集數據,通過監測雲環境,觀察不同雲服務的運行情況,以多參數區間數形式採集雲服務運行的QoS指標數據,列出決策矩陣。其中,多參數區間數是指區間數的參數為三個及以上,傳統的區間數決策問題一般採用由一個最大值和一個最小值兩個參數組成的區間數表示指標數據,這種選取方法缺乏代表性,本發明在傳統區間數基礎上增加了在2/4和3/4兩個百分點所監測到的數據,共同組成一個四參數的區間數,以qik表示多參數區間數,則有:其中,表示在整個檢測過程中檢測到的最小值;表示在第2/4百分點檢測到的數據;表示在第3/4百分點檢測到的數據;表示檢測到的最大值;基於qik的雲服務QoS指標決策矩陣如下所示:
(1-3)將多參數區間數形式的指標值qik轉換成二元聯繫數,得到「均值+最大偏差」二元聯繫數uik,既保存了區間數對範圍的限定作用,又減少了區間數的不確定性,二元聯繫數uik的計算公式如下:
其中,j∈[-1,1];
(1-4)將以複數形式的二元聯繫數uik轉化成等價的三角函數Uik,三角函數成為原區間數的一個代表點。令(cosθ+jsinθ)=1,用三角函數Uik的模rik表示三角函數Uik,則稱rik為三角形的主值,用三角函數的主值代替三角函數參與運算,在保證結果一致性的基礎上,大大簡化運算過程,具體公式表示如下:
(1-5)將步驟(1-4)中進行指標數據轉換後的決策矩陣中的QoS指標數據按照指標的效益型和成本型兩類進行規範化處理,通過規範化處理,可以去除不同QoS指標的量綱,從而實現對不同指標的融合計算;並能夠將不同指標數據轉化為特定區間的數據,避免不同數據數值的巨大波動相互影響。對效益型指標和成本型指標的規範化處理方法是不同的,以r'ik表示規範化後的指標,具體規範化如下:
對效益型指標的規範化處理公式如下:
對成本型指標的規範化處理公式如下:
(1-6)基於對不同QoS指標規範處理後的規範化決策矩陣X'如下:
其中,q'ik=r'ik;i=1,2,...,n;k=1,2,...,m。
步驟(2)所述中基於聯繫數的屬性權重未知的權重設定模塊2,基於步驟(1)求得的規範後的決策矩陣X',指標的權重計算具體步驟如下:
(2-1)定義QoS指標的權重向量集為W=(w1,w2,...,wi,...,wm),並滿足歸一化約束m為指標數量;
(2-2)為了表達指標值的波動性,計算n個雲服務中k個指標值的模的方差,公式如下:
式中,是規範化決策矩陣中雲服務各QoS指標模的平均數;
(2-3)把m個Qk值歸一化處理,計算得到各指標權重ωk,,公式如下:
基於公式(8)求得QoS指標的權重向量集為W=(w1,w2,...,wi,...,wm),並滿足歸一化約束
步驟(3)所述進行雲服務信任評估模塊3,基於所求得規範化決策矩陣和QoS指標權重體系,採用線性加權方法實現對雲服務的信任評估,具體步驟如下:
(3-1)將步驟(1)中所求的規範化決策矩陣X'與步驟(2)中所求得的指標權重向量集W,代入雲服務的信任評估線性加權公式中,計算雲服務的信任評估值,以T(Si)表示第i個雲服務Si的信任評估值,其計算公式如下:
T(Si)=∑(q'ik×wk),i=1,2,...,n;k=1,2,...,m (9)
其中,ωk為步驟(2)中所求得的指標權重集;q'ik為規範化決策矩陣X'中第i行k列的QoS指標數據;採用主值模型進行信任評估,將區間數轉換成二元聯繫數uik,接著,將uik轉化成三角函數,三角函數成為原區間數的一個代表點,用三角函數主值參與信任評估,保存了原區間數對範圍的限定,降低了不確定性,簡化了運算過程;
(3-2)依據步驟(3-1)中的雲服務的信任評估公式,計算各雲服務的信任評估值;進一步對同一雲提供商的不同服務或不同雲提供商的同一服務進行信任評估。
