基於雷電物理的風機葉片動態擊距與電氣幾何模型的構建方法與流程

2023-05-04 16:12:06 1

本發明涉及一種基於雷電物理的風機葉片動態擊距與電氣幾何模型的構建方法。

背景技術：

風電作為清潔能源的重要組成部分，其大規模發展是促進我國能源體系改革的重要技術支撐。然而，鑑於風機所處的環境及其自身特殊結構，極易遭受大氣雷擊。雷擊事故中葉片的損傷佔到雷擊損傷總數的40％以上，且多數為不可修復性損傷。風機葉片的成本、吊裝、維修等高額費用已嚴重影響到風電場的經濟穩定運行。因此，尋找一個可靠的方法評估風機葉片防雷系統的效率，對風機葉片的防雷設計和促進風電的可持續發展具有重要意義。

當前的風機葉片防雷設計多是基於實驗研究，在葉片周圍電場分布、接閃器防護效果等方面取得了一定成果。但實驗室的環境與實際風機的運行環境難免存在差異，其與實際情況的等效性也有待商榷，且對於不同環境、不同型號的風機葉片都需要進行重複試驗，消耗大量的人力物力，亟需發展一種葉片防雷效率的評估方法。

20世紀60年代，國內外學者首次將雷電流的電氣參數與線路的幾何結構聯繫起來研究輸電線路的屏蔽問題，在大量實驗觀測和計算的基礎上推出了輸電線路的經典電氣幾何模型，相對於傳統規程法取得了巨大進步。此後人們對電氣幾何法中的擊距公式進行了改進以適應不同的環境，但是擊距公式依舊存在物理概念模糊，通用性較差的缺點，且不能體現地面物體不同位置、不同結構的擊距變化，難以應用在像風機葉片這樣的複雜旋轉結構。同時，部分現有技術的研究主要是通過先導模型的反覆計算，對指定點的防雷性能指標進行分析，並沒有給出葉片整體的防雷效率計算方法。

技術實現要素：

本發明為了解決上述問題，提出了一種基於雷電物理的風機葉片動態擊距與電氣幾何模型的構建方法，本發明將電氣幾何方法與雷電先導發展的物理過程相結合，提出了針對風機葉片的電氣幾何分析模型。通過引入風機葉片動態擊距的概念及分析方法，使得擊距的物理意義更加清晰，並進一步推導了葉片防雷系統效率的計算方法。隨後利用該模型分析了實際尺寸風機葉片防雷系統效率的影響因素，並基於風機葉片長間隙擊穿實驗驗證了該方法的有效性。提出的風機葉片電氣幾何模型，可為風機葉片的防雷設計與評估提供理論依據。

為了實現上述目的，本發明採用如下技術方案：

一種基於雷電物理的風機葉片動態擊距與電氣幾何模型的構建方法，以雷電先導發展的物理模型為基礎，並以負極性雷擊描述雷擊過程，將負極性雷擊分為三個階段，下行先導向下發展，上行先導起始，上下行先導連接過程，假定雷電下行先導豎直向下發展，當上、下行先導的流注相遇時發生雷擊，將發生雷擊時上行先導流注頭部的高度定為擊距，據此計算出風機葉片動態擊距，以體現風機葉片上不同位置具有不同的擊距，以及風機葉片所處位置的變化而改變擊距，在假設雷電流數值向下發展的前提下，根據動態擊距，建立針對風機葉片的電氣幾何模型。

根據風機葉片電氣幾何模型中暴露弧、屏蔽弧以及風機葉片旋轉角度的幾何關係，計算風機葉片電氣幾何模型暴露距離，進而得到風機葉片防雷系統效率。

風機葉片雷電防護的電氣幾何模型中包括葉片接閃器的擊距、葉片葉身處的擊距、暴露弧和屏蔽弧。

當雷電流幅值增大，暴露弧會持續減小直至消失，葉片得到完全屏蔽，此時所對應的雷電流幅值為葉片可能接閃失敗的最大雷電流。

雷電下行先導採用先導通道電荷分布模型。

利用風機葉片電氣幾何模型，分析風機葉片角度、雷電流幅值和接閃器布置對防雷系統效率的影響，最後基於風機葉片長間隙下擊穿實驗驗證了該模型的有效性。

風機葉片動態擊距的計算方法包括：

1)根據雷雲和下行先導位置，求出風機周圍的背景電位，計算空間電離產生的電荷數，判定電暈起始，若電暈不起始，下行先導進一步向下發展；

2)電暈起始後，由風機周圍電位曲線計算電暈區域電荷，當電暈區域電荷大於設定值時流注向先導轉化，否則下行先導進一步向下發展；

3)先導起始後，假定一個初始先導長度，根據電位畸變曲線計算上行先導發展過程，當上下行先導頭部之間的平均場強為estr時確定接閃，最終求得上行先導和流注的發展高度。

當風機的塔筒高度、雷電流幅值固定時，葉片的擊距與葉片上的位置和旋轉角度有關。

風機防雷系統效率為：

其中，es為葉片防雷系統分級效率，雷電流幅值為i，imin和imax分別為雷電流最小和最大幅值，葉片呈角度θ，f(i)為關於雷電流幅值的概率函數，lmn(i，θ)表示暴露距離的總和，lmo(i，θ)表示總區域距離。

在暴風雨天氣風機停運時，避免有風機葉片接近水平，使葉片豎直向上。增加葉片接閃器時，要考慮接閃器之間的屏蔽效應。

與現有技術相比，本發明的有益效果為：

1)本發明提出了風機葉片動態擊距的概念及分析方法。通過雷電上行先導的物理發展模型，給出了葉片動態擊距的分布特徵，發現接閃器處的擊距有明顯增大，並且該分析方法為具有複雜結構的地面物體防雷提供思路；

2)本發明基於風機葉片動態擊距的概念，該模型將電氣幾何方法與雷電先導發展的物理過程相結合，給出了葉片防雷系統效率的計算方法，為葉片防雷系統的評估提供理論依據，同時設計了風機葉片長間隙擊穿實驗驗證了該模型的有效性；

3)利用構建的模型分析了風機葉片的防雷系統效率，發現雷電流幅值越小、葉片越接近水平葉片防雷系統的效率越低，在暴風雨天氣風機停運時，避免有風機葉片接近水平，使其中一葉片豎直向上。增設葉身接閃器可以有效的提高葉片的防雷效率。

附圖說明

構成本申請的一部分的說明書附圖用來提供對本申請的進一步理解，本申請的示意性實施例及其說明用於解釋本申請，並不構成對本申請的不當限定。

圖1(a)、圖1(b)為本發明的風機葉片動態擊距示意圖；

圖2為本發明的風機葉片雷電防護電氣幾何模型示意圖；

圖3為本發明的雷雲電荷分布模型示意圖；

圖4為本發明的先導發展模型示意圖；

圖5為本發明的i＝30ka時動態擊距曲線示意圖；

圖6為本發明的葉片防雷系統雷電攔截效率分析圖；

圖7為本發明的暴露距離數學計算模型示意圖；

圖8為本發明的不同雷電流幅值下葉片防雷系統失效率示意圖；

圖9為本發明的i＝20ka時動態擊距曲線示意圖；

圖10(a)、圖10(b)分別為本發明在衝擊電流15ka、7.5ka下葉片材料損傷圖；

圖11為本發明不同接閃器數量下葉片防雷系統失效率示意圖；

圖12為本發明的實驗原理圖；

圖13為本發明的放電路徑觀測結果示意圖；

圖14為本發明的計算值與實驗值對比圖。

具體實施方式：

下面結合附圖與實施例對本發明作進一步說明。

應該指出，以下詳細說明都是例示性的，旨在對本申請提供進一步的說明。除非另有指明，本發明使用的所有技術和科學術語具有與本申請所屬技術領域的普通技術人員通常理解的相同含義。

需要注意的是，這裡所使用的術語僅是為了描述具體實施方式，而非意圖限制根據本申請的示例性實施方式。如在這裡所使用的，除非上下文另外明確指出，否則單數形式也意圖包括複數形式，此外，還應當理解的是，當在本說明書中使用術語「包含」和/或「包括」時，其指明存在特徵、步驟、操作、器件、組件和/或它們的組合。

正如背景技術所介紹的，風機遭受雷擊所造成的高額費用已嚴重影響到風電場的經濟穩定運行，尋找一個可靠的方法評估風機葉片防雷系統的效率，對風機葉片的防雷設計和促進風電的可持續發展具有重要意義。現有實驗技術以及仿真模型都不適用於風機複雜的結構以及其旋轉特性，也並沒有給出葉片整體的防雷效率計算方法，為了解決如上的技術問題，本申請提出了一種基於雷電物理的風機葉片動態擊距與電氣幾何模型的構建方法，本發明將電氣幾何方法與雷電先導發展的物理過程相結合，提出了針對風機葉片的電氣幾何分析模型。通過引入風機葉片動態擊距的概念及分析方法，使得擊距的物理意義更加清晰，並進一步推導了葉片防雷系統效率的計算方法。隨後利用該模型分析了實際尺寸(1.5mw)風機葉片防雷系統效率的影響因素，並基於風機葉片長間隙擊穿實驗驗證了該方法的有效性。新提出的風機葉片電氣幾何模型，可為風機葉片的防雷設計與評估提供理論依據。

本申請的一種典型的實施方式中，電氣幾何法可以將雷電流參數同被研究物體的幾何結構聯繫起來，利用擊距描述地面物體的引雷能力，認為雷電下行先導先到達哪個物體的擊距便向哪個物體放電。擊距的物理意義為雷雲向地面發展的先導放電通道頭部到達被擊物體的臨界擊穿距離。在傳統電氣幾何法的擊距計算中，主要是根據運行數據統計，或只通過地面物體周圍的場強來確定擊距，與實際的雷擊過程差距較大。目前廣泛應用的擊距公式僅是雷電流的函數，而實際風機葉片的旋轉結構是在葉片上嵌有一個或多個接閃器，因此，傳統的擊距計算方法無法體現風機葉片接閃器和葉身(無接閃器部分)擊距的不同，另外也不能考慮葉片旋轉角度對擊距的影響，並不適用於風機葉片的防雷計算。

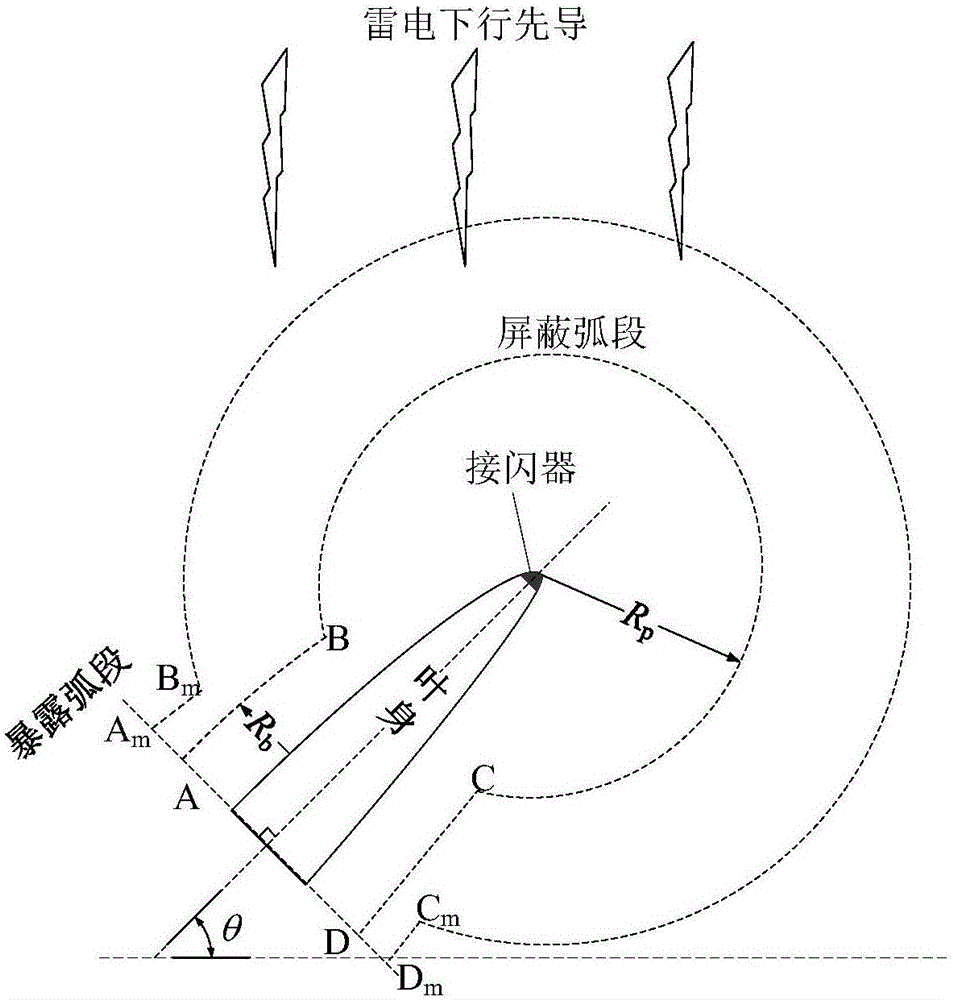
為建立風機葉片的電氣幾何模型，本發明引入風機葉片動態擊距的概念，其「動態」主要包括兩層含義：第一，風機葉片上不同位置(如接閃器和葉身)具有不同的擊距；第二，風機葉片所處位置(如角度和高度)的變化，也會引起擊距的變化。風機葉片的動態擊距具有分布特徵，不僅接閃器處存在擊距，葉身處也有對應的擊距，只是葉身的擊距較短，在葉片的平面內可看作距離葉身表面一定距離、曲率較小的非圓弧。圖1(a)、圖1(b)給出了不同角度和葉片上不同位置擊距的變化情況。當葉片非豎直向上時，兩側擊距不是嚴格對稱的，下側的擊距(如圖1(a)所示)略小於上側的擊距。當假設雷電豎直向下發展時，下側擊距不會影響接閃，考慮到葉片的旋轉對稱性，將葉片上側擊距關於葉片軸線對稱到下側，便於模型的數值計算。

根據上述風機葉片的動態擊距概念，可推導風機葉片雷電防護的電氣幾何模型，如圖2所示，假設雷電下行先導豎直向下發展。其中，rp為葉片接閃器的擊距，rb為葉片葉身處的擊距，θ為風機葉片與水平方向的夾角，取逆時針方向為正。當雷電流幅值為i時，葉片的擊距對應於弧其中弧為暴露弧，為屏蔽弧，a點為所研究葉片部分(可以是葉片一部分)對應擊距包絡線的起始點。當雷電下行先導到達暴露弧時，則表示葉身遭受雷擊，防雷系統接閃失敗。

隨著雷電流的增加，rp和rb也隨之增大，當雷電流增加到im時，擊距範圍增加到可以看到暴露弧相對於雷電流i時的暴露弧明顯減小，當雷電流幅值繼續增大，暴露弧會繼續減小至消失，葉片得到完全屏蔽，此時所對應的雷電流幅值為葉片可能接閃失敗的最大雷電流imax。當雷電流的幅值大於imax時，葉片的防雷系統能夠對葉片完全屏蔽，imax主要與葉片所處位置及葉片防雷系統的設計有關。對於一個已經設計好的風機葉片防雷系統，其不能有效屏蔽的雷電流的幅值範圍是imin<i<imax，其中imin為使葉片擊穿時材料不受損傷的最大雷電流幅值，imin主要與葉片所用材料及加工工藝有關。若葉片防雷系統設計的防護能力足夠強，使得imax1μc時流注向先導轉化，否則下行先導進一步向下發展；

3)先導起始後，假定初始先導長度0.05m，根據電位畸變曲線(8)計算上行先導發展過程，當上下行先導頭部之間的平均場強為estr時確定接閃，最終求得上行先導和流注的發展高度。

本發明計算中為減小計算量，認為上行先導長度>2m可形成穩定上行先導。上下行先導發展的整體速度比在1:4～1:1之間變化，對於自然界雷擊這樣的超長間隙放電，計算發現其整體速度比更接近1:4。由上行先導穩定起始時下行先導的對地高度，結合速度比可給出動態擊距的近似值。由先導模型，當雷電流為30ka，下行先導步長為10m，速度比取1:4時得到風機葉片的動態擊距曲線如圖5所示，可以看出當塔筒高度、雷電流幅值固定時，葉片的擊距與葉片上的位置和旋轉角度有關。

風機葉片的動態擊距曲線如圖5所示，可分為三個區域，在尖端效應區存在明顯的上翹，這是由葉尖接閃器尖端效應導致的，接閃器周圍的空間電位畸變嚴重，更容易產生上行先導，所以其擊距明顯大於葉身處。葉身區域擊距隨距葉片尖端距離的增加而減小，可近似用一條斜向下的直線表示葉身擊距rb(l)，l表示距葉尖距離，如圖5中的虛線所示。虛線與橫坐標方向的夾角為θ'，我們稱之為葉身動態擊距擬合角，為負值。在屏蔽效應區，由於風機塔筒屏蔽效應，擊距下降速度加快，該現象在葉片角度越接近水平時越明顯。ieee根據大量現場運行數據推薦的擊距公式在地面物體防雷中有廣泛應用，但只能給出風機葉片豎直向上時葉尖接閃器的擊距，利用ieee推薦公式計算葉尖接閃器擊距為72.9m，與本發明擊距模型得到葉尖接閃器擊距67m比較接近，證明了本發明擊距模型的可靠性。

電氣幾何法自提出以來經過了不斷改進，1993年ieee工作組基於長期的數據統計和研究，提出了採用暴露距離的方法來計算防雷系統的攔截效率，該方法同樣假定下行先導豎直向下發展，與本發明先前做的假設一致。其中暴露距離是指暴露弧兩端點之間的水平距離，如圖6所示。

iec61400-24中提出風機防雷系統效率e的計算公式：

e＝ei×es(9)

式中ei為風機葉片的攔截效率，es為葉片防雷系統分級效率。

當雷電流幅值為i，葉片呈角度θ時，根據暴露距離法得葉片的攔截效率ei：

當雷電流幅值imin<i<imax，由式(9)、式(10)得到風機葉片與水平方向呈角度θ時，葉片防雷系統效率為：

式中f(i)為關於雷電流幅值的概率函數；對於有多接閃器的風機葉片，lmn表示暴露距離的總和。

在實際風機運行中，風機葉片處於不斷旋轉狀態，式(11)中的各距離不僅是i的函數，也是θ的函數。考慮到風機旋轉過程以及葉片在0-180°時更易遭受雷擊，令式(11)在0-180°內幾何平均值作為運行風機葉片防雷系統效率：

在此我們認為防雷系統洩流容量足夠大，只要接閃器接閃成功則不會對葉片造成損傷，則es取值為1。

暴露距離lmn是獲得風機葉片防雷系統效率的重要參數。下面將以兩接閃器葉片暴露距離計算為例，說明風機葉片暴露距離計算方法。由於葉片的旋轉具有旋轉對稱性，計算中θ取值為0-90°。

葉片具有側接閃器時擊距的包絡範圍如圖7所示。l1、l2分別表示兩接閃器和接閃器到所研究葉片起點間的距離；屏蔽弧分別為以葉尖接閃器和葉身接閃器為圓心，兩接閃器擊距rp1、rp2為半徑的圓弧；暴露弧到葉身的垂直距離為葉身的擊距rb(l)，暴露距離即a1、b1和c1、d1水平距離的和。所研究葉片起點處o的葉身擊距為rb(l1+l2)，令a1點坐標為(x1,y1)，則有：

葉片同一側暴露弧(如)可近似認為在同一條直線上，a1、b1、c1、d1所在的直線為：

式中θ'為葉身動態擊距擬合角(圖5中給出)。o1、o2的坐標為：

則o1、o2所在圓的方程為：

聯立式(14)、式(16)可以求得坐標b1(x2,y2)、c1(x3,y3)、d1(x4,y4)的數值，根據葉片動態擊距作出電氣幾何模型圖，可確定各點位置。對於圖7所示存在兩端暴露弧的情況，需要捨棄x值最大的一組解且有x2<x31.8m)，模型將接閃成功率低於一定值當作完全不能防護處理，保證了葉片電氣幾何模型的保護域度，但在過渡區域內有一定的誤差。

從整體上看，計算曲線與實驗擬合曲線形狀接近，具有一定的保護域度，只有在過渡區域存在一定誤差。實驗證明了本發明風機葉片電氣幾何模型的有效性。

需要說明是，實驗條件與真實風機的雷擊環境難免存在差別，實驗與實際情況的等效性仍需要驗證，但所設計的實驗一定程度上證明了本發明方法的可靠性。

以上所述僅為本申請的優選實施例而已，並不用於限制本申請，對於本領域的技術人員來說，本申請可以有各種更改和變化。凡在本申請的精神和原則之內，所作的任何修改、等同替換、改進等，均應包含在本申請的保護範圍之內。

上述雖然結合附圖對本發明的具體實施方式進行了描述，但並非對本發明保護範圍的限制，所屬領域技術人員應該明白，在本發明的技術方案的基礎上，本領域技術人員不需要付出創造性勞動即可做出的各種修改或變形仍在本發明的保護範圍以內。