一種基於狀態估計性能評估的聚集度度量方法及系統與流程
2023-05-18 09:22:41 1
本發明涉及目標跟蹤狀態估計技術的性能評估領域,具體涉及一種基於狀態估計性能評估的聚集度度量方法及系統。
背景技術:
隨著估計理論及算法的發展,為了更好的理解、開發和比較估計算法,對估計器性能的評估變的日益重要。不同角度的性能比較可以幫助工程人員得到更好的理解以及擇選更好更符合需求的估計器。現有的性能評估一般都是基於估計誤差的2-範數——均方根誤差(rmse)來描述的。但是,這一指標常不是那麼理想。首先,在估計誤差帶來的損失不知道或者不好描述時,很難對估計誤差進行量化。其次,參考的性能很容易受估計誤差量化方式的影響。以軍事應用中飛彈攔截或者摧毀目標為例,要關心的不是平均誤差而是估計量應當在被估量的一個鄰域內,才能保證目標被擊中。
為了克服上述現有評估指標的缺點,本發明的目的在於提供一種基於聚集度理論的狀態估計技術性能評估的度量方法,提出了衡量估計誤差聚集程度的度量準則。
技術實現要素:
本發明引入相對聚集度,即度量誤差的概率密度函數相對於期望的分布的聚集度進行對比,克服了現有評估指標評估不精確的缺點。
本發明提供了一種基於狀態估計性能評估的聚集度度量方法,其特徵在於:
通過數據獲取單元,獲取待評估狀態下的估計誤差數據集;
通過相對聚集度計算單元,估計誤差數據集進行計算,得到待評估狀態的二維高斯概率密度模型和誤差的相對聚集度;
通過第一理想狀態對比單元,考慮估計誤差期望分布為均值為零的均勻分布的條件下,將相對聚集度與期望分布的誤差聚集對比得到該待評估狀態的聚集度度量結果;
通過第二理想狀態對比單元,考慮估計誤差期望分布為拉普拉斯分布的條件下,將相對聚集度與拉普拉斯分布對比得到該待評估狀態的聚集度度量結果;
通過第三理想狀態對比單元,考慮估計誤差期望分布不存在的情況,提出一種估計誤差絕對聚集程度度量方法,引入基於誤差自相關係數的聚集度指標,對比後得到該評估狀態的聚集度度量結果;
通過度量結果輸出單元,輸出最終聚集度度量結果。
進一步地,計算待評估狀態的誤差的相對聚集度時,有基於以下公式的數學模型:
考慮估計誤差服從高斯分布
其等高線由下式定義
描述了給定t的一個橢球。這一橢球體積隨著t的增大而增大,t落在橢球外面的概率由t唯一確定]
式中k是x的維度。這一概率隨著t的增加而減小,即,點離橢球中心越來越遠,這一概率越大,也就說明誤差點離中心越近,即越聚集。因此這一概率刻畫了點落入橢球的百分比。在這一意義下,這一概率可以理解為在橢球邊界上的點的聚集度,滿足幾何上,這一邊界對應高斯分布的等高線。類似地,概率p(t<t)可以理解為點的離散度。
概率p(t>t)和概率p(t<t)分別是橢圓邊界上對應點的聚集度和離散度,因此,對誤差集合每一個點都有各自的聚集度和離散度假設估計誤差概率密度函數為則估計誤差的相對聚集度為
進一步地,在第一理想狀態對比單元內,有基於以下公式的數學模型:
在一維情況下,選取期望分布為a>0。則集合的各點的相對聚集度為
假設中各誤差相互獨立,則有
式中,m<n為落在期望分布內的點數。
在二維情況下,取估計器誤差分布期望函數為均勻分布,表達式如下
則集合各點的相對聚集度為
假設中各誤差相互獨立,則有
在高維情況下,仍取期望分布為對稱的m維均勻分布,
則集合中誤差在相對獨立的條件下,相對聚集度為
進一步地,在第二理想狀態對比單元內,有基於以下公式的數學模型:
拉普拉斯分布在一維情況下的表達式為
在誤差分布服從拉普拉斯分布時,取為期望分布時,一般情況下,取均值μ=0,則有
假設中各誤差相互獨立,則有
在高維情況下,由於高維拉普拉斯函數積分比較困難,可對各誤差點求歐幾裡得範數,即εi=||xi||,進而可以按一維情況求近似相對聚集度。
進一步地,在第三理想狀態對比單元內,有基於以下公式的數學模型:
基於估計誤差自相關係數的聚集度指標
式中w=∑i∑jwij。可以按照實際場景中的要求進行設計,若要求最大距離為l,則可定義
式中可根據實際需要選取相應範數,這一指標可以求得估計誤差自身的相關性,相關性越大也就理解為越聚集。
本發明還提供了一種基於狀態估計性能評估的聚集度度量系統,其特徵在於,包括:
通過數據獲取單元,獲取待評估狀態下的估計誤差數據集;
通過相對聚集度計算單元,估計誤差數據集進行計算,得到待評估狀態的二維高斯概率密度模型和誤差的相對聚集度;
第一理想狀態對比單元,用以考慮估計誤差期望分布為均值為零的均勻分布的條件下,將相對聚集度與期望分布的誤差聚集對比得到該待評估狀態的聚集度度量結果;
第二理想狀態對比單元,用以考慮估計誤差期望分布為拉普拉斯分布的條件下,將相對聚集度與拉普拉斯分布對比得到該待評估狀態的聚集度度量結果;
第三理想狀態對比單元,用以考慮估計誤差期望分布不存在的情況,提出一種估計誤差絕對聚集程度度量方法,引入基於誤差自相關係數的聚集度指標,對比後得到該評估狀態的聚集度度量結果;
度量結果輸出單元,用以輸出最終聚集度度量結果。
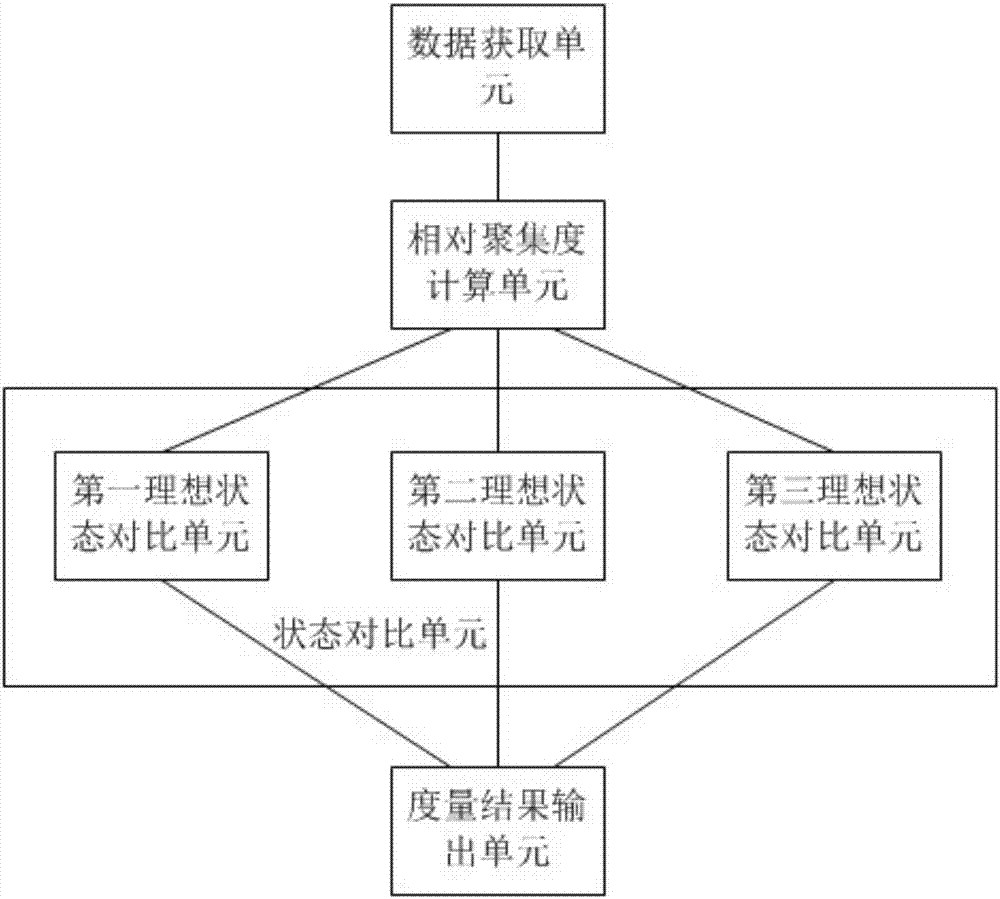
進一步地,所述數據獲取單元電連接於所述相對聚集度計算單元,所述相對聚集度計算單元分別與所述第一理想狀態對比單元、所述第二理想狀態對比單元和所述第三理想狀態對比單元電連接,所述第一理想狀態對比單元電連接於所述度量結果輸出單元,所述第二理想狀態對比單元電連接於所述度量結果輸出單元,所述第三理想狀態對比單元電連接於所述度量結果輸出單元。
本發明的有益效果為:
本發明引入相對聚集度,即度量誤差的概率密度函數相對於期望的分布的聚集度進行對比,克服了現有的性能評估基於估計誤差的2-範數——均方根誤差(rmse)來描述的時,指標不理想的缺點,更有效的優化了評估效果。
附圖說明
圖1為本發明的系統連接示意圖;
具體實施方式
下面將結合附圖對本發明的技術方案進行清楚、完整地描述,顯然,所描述的實施例是本發明一部分實施例,而不是全部的實施例。基於本發明中的實施例,本領域普通技術人員在沒有做出創造性勞動前提下所獲得的所有其他實施例,都屬於本發明保護的範圍。
在本發明的描述中,需要說明的是,術語「中心」、「上」、「下」、「左」、「右」、「豎直」、「水平」、「內」、「外」等指示的方位或位置關係為基於附圖所示的方位或位置關係,僅是為了便於描述本發明和簡化描述,而不是指示或暗示所指的裝置或元件必須具有特定的方位、以特定的方位構造和操作,因此不能理解為對本發明的限制。此外,術語「第一」、「第二」、「第三」僅用於描述目的,而不能理解為指示或暗示相對重要性。
在本發明的描述中,需要說明的是,除非另有明確的規定和限定,術語「安裝」、「相連」、「連接」應做廣義理解,例如,可以是固定連接,也可以是可拆卸連接,或一體地連接;可以是機械連接,也可以是電連接;可以是直接相連,也可以通過中間媒介間接相連,可以是兩個元件內部的連通。對於本領域的普通技術人員而言,可以具體情況理解上述術語在本發明中的具體含義。
如圖1所示,本發明提供了一種基於狀態估計性能評估的聚集度度量方法,其特徵在於:
通過數據獲取單元,獲取待評估狀態下的估計誤差數據集;
通過相對聚集度計算單元,估計誤差數據集進行計算,得到待評估狀態的二維高斯概率密度模型和誤差的相對聚集度;
通過第一理想狀態對比單元,考慮估計誤差期望分布為均值為零的均勻分布的條件下,將相對聚集度與期望分布的誤差聚集對比得到該待評估狀態的聚集度度量結果;
通過第二理想狀態對比單元,考慮估計誤差期望分布為拉普拉斯分布的條件下,將相對聚集度與拉普拉斯分布對比得到該待評估狀態的聚集度度量結果;
通過第三理想狀態對比單元,考慮估計誤差期望分布不存在的情況,提出一種估計誤差絕對聚集程度度量方法,引入基於誤差自相關係數的聚集度指標,對比後得到該評估狀態的聚集度度量結果;
通過度量結果輸出單元,輸出最終聚集度度量結果。
進一步地,計算待評估狀態的誤差的相對聚集度時,有基於以下公式的數學模型:
考慮估計誤差服從高斯分布
其等高線由下式定義
描述了給定t的一個橢球。這一橢球體積隨著t的增大而增大,t落在橢球外面的概率由t唯一確定]
式中k是x的維度。這一概率隨著t的增加而減小,即,點離橢球中心越來越遠,這一概率越大,也就說明誤差點離中心越近,即越聚集。因此這一概率刻畫了點落入橢球的百分比。在這一意義下,這一概率可以理解為在橢球邊界上的點的聚集度,滿足幾何上,這一邊界對應高斯分布的等高線。類似地,概率p(t<t)可以理解為點的離散度。
概率p(t>t)和概率p(t<t)分別是橢圓邊界上對應點的聚集度和離散度,因此,對誤差集合每一個點都有各自的聚集度和離散度假設估計誤差概率密度函數為則估計誤差的相對聚集度為
進一步地,在第一理想狀態對比單元內,有基於以下公式的數學模型:
在一維情況下,選取期望分布為a>0。則集合的各點的相對聚集度為
假設中各誤差相互獨立,則有
式中,m<n為落在期望分布內的點數。
在二維情況下,取估計器誤差分布期望函數為均勻分布,表達式如下
則集合各點的相對聚集度為
假設中各誤差相互獨立,則有
在高維情況下,仍取期望分布為對稱的m維均勻分布,
則集合中誤差在相對獨立的條件下,相對聚集度為
進一步地,在第二理想狀態對比單元內,有基於以下公式的數學模型:
拉普拉斯分布在一維情況下的表達式為
在誤差分布服從拉普拉斯分布時,取為期望分布時,一般情況下,取均值μ=0,則有
假設中各誤差相互獨立,則有
在高維情況下,由於高維拉普拉斯函數積分比較困難,可對各誤差點求歐幾裡得範數,即εi=||xi||,進而可以按一維情況求近似相對聚集度。
進一步地,在第三理想狀態對比單元內,有基於以下公式的數學模型:
基於估計誤差自相關係數的聚集度指標
式中w=∑i∑jwij。可以按照實際場景中的要求進行設計,若要求最5大距離為l,則可定義
式中可根據實際需要選取相應範數,這一指標可以求得估計誤差自身的相關性,相關性越大也就理解為越聚集。
本發明還提供了一種基於狀態估計性能評估的聚集度度量系統,其特徵在於,包括:
通過數據獲取單元,獲取待評估狀態下的估計誤差數據集;
通過相對聚集度計算單元,估計誤差數據集進行計算,得到待評估狀態的二維高斯概率密度模型和誤差的相對聚集度;
第一理想狀態對比單元,用以考慮估計誤差期望分布為均值為零的均勻分布的條件下,將相對聚集度與期望分布的誤差聚集對比得到該待評估狀態的聚集度度量結果;
第二理想狀態對比單元,用以考慮估計誤差期望分布為拉普拉斯分布的條件下,將相對聚集度與拉普拉斯分布對比得到該待評估狀態的聚集度度量結果;
第三理想狀態對比單元,用以考慮估計誤差期望分布不存在的情況,提出一種估計誤差絕對聚集程度度量方法,引入基於誤差自相關係數的聚集度指標,對比後得到該評估狀態的聚集度度量結果;
度量結果輸出單元,用以輸出最終聚集度度量結果。
進一步地,所述數據獲取單元電連接於所述相對聚集度計算單元,所述相對聚集度計算單元分別與所述第一理想狀態對比單元、所述第二理想狀態對比單元和所述第三理想狀態對比單元電連接,所述第一理想狀態對比單元電連接於所述度量結果輸出單元,所述第二理想狀態對比單元電連接於所述度量結果輸出單元,所述第三理想狀態對比單元電連接於所述度量結果輸出單元。
本發明引入相對聚集度,即度量誤差的概率密度函數相對於期望的分布的聚集度進行對比,克服了現有的性能評估基於估計誤差的2-範數——均方根誤差(rmse)來描述的時,指標不理想的缺點,更有效的優化了評估效果。
最後應說明的是:以上各實施例僅用以說明本發明的技術方案,而非對其限制;儘管參照前述各實施例對本發明進行了詳細的說明,本領域的普通技術人員應當理解:其依然可以對前述各實施例所記載的技術方案進行修改,或者對其中部分或者全部技術特徵進行等同替換;而這些修改或者替換,並不使相應技術方案的本質脫離本發明各實施例技術方案的範圍。
