導向矢量失配情況下基於稀疏表示的波達方向估計方法與流程
2023-05-10 14:31:46 4
本發明屬於陣列信號處理領域,具體涉及到提出了一種在非理想高斯噪聲環境中,傳感器導向矢量適配情況下,利用稀疏表示方法進行信號源波達方向估計的算法。
背景技術:
信號源波達方向(DOA)估計一直是目標定位和追蹤領域的重要研究方向之一,在雷達、聲納、災害學、通信等方面都有著極大的應用。近些年來隨著人們在航天、海洋、災害預測等領域的研究日益深入,目標DOA估計受到更加廣泛的關注,並被實際應用在空間目標追蹤、水聲通信、管線保護和地震預測等領域。
對DOA估計的研究經歷了很長的發展歷程,產生了一系列經典的的估計算法,比如Capon,MUSIC和ESPRIT等,但這些算法在信噪比較低、快拍數較少的情況下信號的解析度和測向精度下降嚴重。近些年來,基於信號在空間分布的稀疏性特點,研究人員將稀疏重構的思想應用在DOA估計方面,並提出了一些基於稀疏表示的DOA估計算法。早期稀疏表示方法是通過構建僅與信號源DOA相關的累積量域數據,利用加權l1範數最小化方法進行DOA估計,並在此基礎上對DOA估計值進行稀疏化用於估計距離參數,該方法能夠有效地避免信號源物理距離相近對DOA估計產生的影響。最近研究人員提出利用聚焦方法思想提出了一種基於稀疏表示的寬帶信號源DOA估計算法(FSP),用單一頻點的基矩陣代替頻率和角度聯合構建的基矩陣,減少了基矩陣的列數,解決了傳統稀疏表示方法中由於基矩陣維數過大而使得存儲量大以及計算複雜等難題。已有研究人員在實際環境中利用稀疏表示方法驗證DOA估計的性能,根據嵌套陣和互素陣兩種陣列的陣型結構推導出稀疏陣列信號處理模型,採用空域等角度稀疏和等正弦空間稀疏兩種模型進行DOA估計,這種方法能夠用較少的陣元達到較大的自由度,從而提高目標分辨的精度,但並未考慮實際環境中不穩定因素對接收信號產生的影響。
在一些實際環境中,由於噪聲分量重尾現象比較嚴重,因此需要選擇一個合適的噪聲模型用於噪聲信號處理,通常採用的是衝擊噪聲或者SαS噪聲進行模擬,而本發明採用合成圓對稱廣義高斯分布來模擬噪聲環境,它的衰減速率更加緩慢,能夠更加真實地描述實際環境噪聲分布。同時在實際應用中,由於受到自身以及外界環境因素的影響,傳感器的導向矢量可能會產生波動,生成一個非理想增益,使之與真實值之間存在誤差,這對DOA估計的精確度會產生很大的影響。
技術實現要素:
為克服現有技術的不足,本發明旨在實現在傳感器導向矢量失配的情況下利用稀疏表示方法對信號源波達方向進行估計。本發明採用的技術方案是,導向矢量失配情況下基於稀疏表示的波達方向估計方法,首先構建傳感器陣列的接收信號模型;然後採用合成圓對稱廣義高斯分布對重尾嚴重的實際環境噪聲信號進行模擬,利用分數低階矩方法對接收信號模型進行處理,並對處理後的信號模型中存在的未知增益值即導向矢量失配而生成的不確定參數增益值進行優化;最後,採用基於稀疏表示方法進行信號源波達方向DOA估計,得到最優的信號源波達方向DOA估計值。
首先構建傳感器陣列的接收信號模型,假設處於遠場環境下的Q個窄帶隨機信號源發射的信號波到達由P個傳感器組成的均勻線性陣列ULA,其中Q個信號源之間相互獨立,並且噪聲與信號互不相關;第q個信號源的到達角記為θq,在t時刻,第p個傳感器處的接收信號為式中,a(θq)為第q個信號源sq(t)在其波達方向θq上第p個傳感器處的導向矢量,表達式為d為傳感器之間的距離,λ為信號波長,gp為實際環境中第p個傳感器處的導向矢量增益值,sq(t)為空間中隨機分布的窄帶信號,np(t)為空間噪聲信號;
根據每個傳感器處的接收信號求得傳感器陣列的接收信號模型:
x(t)=GAs(t)+n(t)
其中
x(t)=[x1(t),x2(t),...,xP(t)]T
G=diag[g1,g2,...,gP]
A=[a(θ1),a(θ2),...,a(θQ)]
s(t)=[s1(t),s2(t),...,sq(t)]T
n(t)=[n1(t),n2(t,...,np(t))]T
式中,x(t)為傳感器陣列接收信號模型,[·]T表示陣列轉置,G是各個傳感器處的增益值組成的對角陣,A為所有導向矢量組成的陣列流形,a(θq)為各個傳感器在信號源q處的導向矢量,s(t)為信號源矩陣,sq(t)為第q個信號源的發射信號,n(t)為所有傳感器處的噪聲信號,np(t)為第p個傳感器處的噪聲信號。
採用合成圓對稱廣義高斯分布來模擬實際噪聲環境,噪聲信號關於隨機變量w的概率密度函數表示為:
式中,Γ(·)表示伽馬函數,α為穩定分布係數,σ為函數方差,並且當α=2時,噪聲呈現高斯分布。
採用基於分數低階矩矩陣方法FLOM對其進行處理,具體步驟如下:均勻線性傳感器陣列的接收信號x(t)分數低階矩矩陣是一個P×P的矩陣,它的第(i,k)個分量為
式中,E(·)表示期望值,x*(t)表示其共軛函數,x(t)中各個信號之間互不相關,ε為小於α的指數參數;
將信號時域模型代入到傳感器陣列接收信號x(t)的分數低階矩矩陣表達式中
將Rik分解為兩部分Cik和Dik,其中
式中,為克羅內克符號,i,k為分數低階矩矩陣分量的下標,θq,θr分別為第q個和第r個信號源的到達角,sq(t),sr(t)分別為第q和第r個信號源的發射信號,且在上式中
因此,傳感器陣列的分數低階矩矩陣表示為
R=GAΓAH+γI
式中,I為P×P階的單位矩陣,A為陣列流形矩陣,H表示共軛轉置。
由於上式中含有傳感器自身運動以及外界環境幹擾產生的增益值G,利用加權最小二乘方法對其進行最優化估計,求出其最優解:首先將得到的傳感器陣列接收信號x(t)按照時間間隔T進行K次採樣得到採樣信號x(n),則得到其協方差矩陣的表達式
根據獲取到的採樣數據,利用加權最小二乘法得到增益函數,再通過求取增益函數的最小值來獲得無定向增益的最優解
式中,W是權重係數,通這裡先利用W=Ι對其進行初始化,之後用對每次的採樣數據進行修改,則上式中的增益函數改寫為
由於傳感器陣列是由P個傳感器組成的,則第p個傳感器處的增益函數記為:
式中,wn=ζ(Wn)且z=ζp(GAΓAH)/gp,其中操作符ζp(·)表示從一個矩陣中選擇其第p列作為列向量,並去掉向量中第p個元素。
這樣最優增益值求解問題就轉化為求解P個線性最小二乘問題,然後對增益函數求最小值來求得最終結果,在這裡引入公式zw=z⊙wn,則求出的最優增益值為
最後,基於稀疏表示方法進行DOA估計,具體步驟是:首先對增益值優化後的信號模型進行矢量化處理;在得到矢量化的分數低階矩矩陣之後,對DOA角度進行稀疏化處理,構造冗餘的角度集合,並採用奇異值分解SVD的方法得到信號子空間,將角度求解轉化為二階錐規劃問題。
對增益值優化後的分數低階矩矩陣進行矢量化
式中,vec表示矢量化運算,和⊙分別表示矩陣的Kronecker積和Khatri-Rao積。
則K個採樣幀內所有的分數低階矩矩陣矢量化後得
式中,yk為每個採樣幀內的矢量化分數低階矩矩陣,定義由於響應矩陣矩陣Y的維數變為P2,可測得的信號源數目Q與陣元數P需滿足Q≤2(P-1)。
在得到矢量化的分數低階矩矩陣之後,採用稀疏表示方法對DOA角度進行冗餘化處理,稀疏表示DOA估計方法的主要思想是用角度集合覆蓋所有可能的目標信號入射方向,且滿足N>>Q,N是劃分的空間角度的個數,基於此可構成一個過完備的冗餘字典它包含源的所有可能的位置信息,採取某些方法從這些位置信息中提取到所需的角度信息,採用奇異值分解SVD的方法對K幀內的矢量化分數低階矩矩陣進行處理
式中,和分別為左奇異矩陣和右奇異矩陣,為對角陣;
得到信號子空間
式中,I為Q×Q階的單位矩陣,
因此,將信號源DOA求解問題轉化為
式中,||·||1和||·||2分別表示l1範數和l2範數,規則化參數β用來平衡信號稀疏性和噪聲的影響;
根據陣列輸出數據的有限快拍數只能得到的估計結果並且它們近似相等把上式的最優化問題轉化為
式中,參數λ用來平衡l1範數和l2範數,目標函數的前一項反映失配程度,後一項反映稀疏性要求,上式是一個二階錐規劃問題,利用內點法進行求解,進而根據非零元素的位置求得信號源的DOA估計值。
本發明的特點及有益效果是:
1.本發明考慮實際環境中噪聲重尾嚴重時利用合成圓對稱廣義高斯分布進行模擬,並採用分數低階矩矩陣對信號模型進行處理,克服了此噪聲環境下,噪聲二階以上矩不存在時傳統算法不能進行準確估計的缺點;
2.本發明對實際環境中傳感器導向矢量非理想的情況進行處理,利用加權最小二乘方法對導向矢量增益值進行優化估計;
3.本發明克服了傳統DOA估計算法中當傳感器數目少於源數目時不能進行精確DOA估計的問題;
4.本發明利用改進的稀疏表示算法進行信號源DOA估計,提高了估計精度,並採用奇異值分解降低了運算量。
附圖說明:
附圖1是本發明算法的方向流程圖;
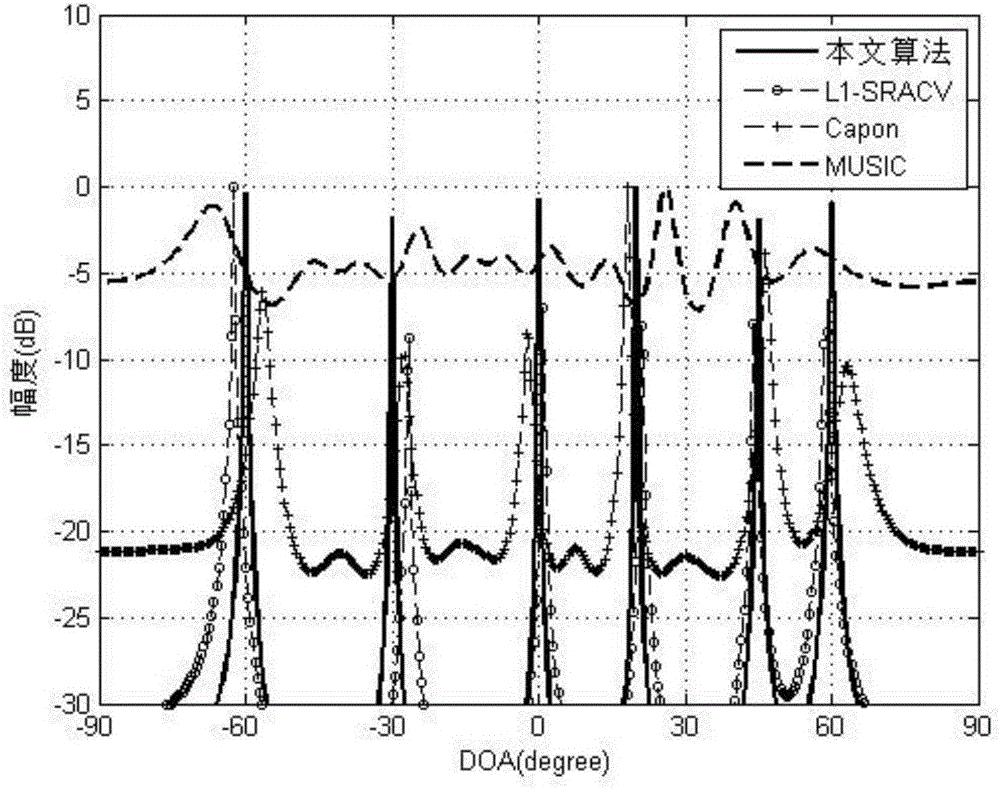
附圖2是本發明算法及其它經典算法的DOA估計結果;
附圖3是信號DOA估計的均方誤差與信噪比的關係曲線;
附圖4是信號DOA估計的均方誤差與快拍數的關係曲線;
附圖5是信號DOA估計的檢測概率與信噪比的關係曲線。
具體實施方式:
針對現有技術的問題,本發明提出了一種新的基於稀疏表示的DOA估計算法。該算法選用合成圓對稱廣義高斯分布模擬實際環境噪聲,但由於其二階以上矩都不存在,傳統的基於協方差矩陣分解的算法不再適用,因此本發明算法採用基於分數低階矩陣的方法對噪聲信號進行處理。然後對導向矢量失配而生成的增益值,利用加權最小二乘法進行優化估計。最後採用稀疏表示方法構建過完備的冗餘字典,並利用奇異值分解降低維數,將其轉化為二階錐規劃問題進行求解,利用內點法得到最優的DOA估計值。
本發明主要解決的問題是在傳感器導向矢量失配的情況下利用稀疏表示方法對信號源波達方向進行估計。本發明的實現過程如下:
步驟一:構建信號模型。
假設處於遠場環境下的Q個窄帶隨機信號源發射的信號波到達由P個傳感器組成的均勻線性陣列(ULA),其中這Q個信號源之間相互獨立,並且噪聲與信號互不相關。第q個信號源的到達角記為θq,在t時刻,第p個傳感器處的接收信號為式中,a(θq)為信號sq(t)在其波達方向θq上第p個傳感器處的導向矢量,表達式為d為傳感器之間的距離,λ為信號波長。gp為實際環境中第p個傳感器處的導向矢量增益值,sq(t)為空間中隨機分布的窄帶信號,np(t)為空間噪聲信號。
根據每個傳感器處的接收信號可以求得傳感器陣列的接收信號模型
x(t)=GAs(t)+n(t)
其中
x(t)=[x1(t),x2(t),...,xP(t)]T
G=diag[g1,g2,...,gP]
A=[a(θ1),a(θ2),...,a(θQ)]
s(t)=[s1(t),s2(t),...,sQ(t)]T
n(t)=[n1(t),n2(t,...,nP(t))]T
式中,x(t)為傳感器陣列接收信號模型,G是各個傳感器處的增益值組成的對角陣,A為所有導向矢量組成的陣列流形,a(θq)為各個傳感器在信號源q處的導向矢量,s(t)為信號源矩陣,sq(t)為第q個信號源的發射信號,n(t)為所有傳感器處的噪聲信號,np(t)為第p個傳感器處的噪聲信號。
步驟二:基於分數低階矩的信號模型處理及增益值最優化估計。
實際環境中的噪聲信號不總是理想的高斯白噪聲,這會對目標角度估計產生一定的影響,尤其是在噪聲重尾現象比較嚴重時這種影響尤為突出。針對此情況我們採取以下步驟進行解決:首先採用合成圓對稱廣義高斯分布對重尾嚴重的噪聲信號進行模擬,並利用分數低階矩方法處理接收信號模型,接下來對信號模型中存在的未知增益值進行優化。
一些實際環境中的噪聲分量重尾現象非常地嚴重,在進行噪聲處理時需要選擇合適的分布類型對其進行模擬,通常採用的是衝擊噪聲或者SαS噪聲分布類型,而本發明採用合成圓對稱廣義高斯分布來模擬噪聲環境,它的衰減速率更加緩慢,能夠更加真實地描述實際環境噪聲分布。噪聲信號關於隨機變量w的概率密度函數表示為
式中,Γ(·)表示伽馬函數,α為穩定分布係數,σ為函數方差,並且當α=2時,噪聲呈現高斯分布。
由於噪聲信號為合成圓對稱廣義高斯噪聲時,接收信號協方差矩陣的二階以上矩不存在,因此傳統的MUSIC、ESPRIT等基於協方差矩陣特徵分解的DOA估計算法都不再適用。這裡我們採用分數低階矩矩陣(FLOM)方法對噪聲分量進行處理。
均勻線性傳感器陣列的接收信號x(t)分數低階矩矩陣是一個P×P的矩陣,它的第(i,k)個分量為式中,E(·)表示期望值,x*(t)表示其共軛函數,x(t)中各個信號之間互不相關。
由於FLOM矩陣中存在因導向矢量失配而生成的不確定參數增益值g,這對後續數據的處理造成極大的困擾,因此我們需要採取合理的方法對其包含的g值進行估計,求出其最優解。在本發明中我們利用加權最小二乘方法迭代求出最優增益值。通過求取增益函數的最小值來獲得無定向增益的最優解式中,W是權重係數,通常情況下是未知的,但由於在實際環境中,環境噪聲對信號處理的影響會比較大,因此這裡先利用W=Ι對其進行初始化,之後用對每次的採樣數據進行修改。
步驟三:基於稀疏表示方法進行DOA估計。
在實際應用中我們經常會遇到傳感器數目少於信號源數目的情況,這時利用傳統的DOA估計方法不再能夠進行精確測量,針對這種情況本文採取矢量化方法進行處理,增加FLOM矩陣的維數,進而增加可測得的源數目。
在得到矢量化的分數低階矩矩陣之後,採用稀疏表示方法對DOA角度進行冗餘化處理。稀疏表示DOA估計方法的主要思想是將包含導向矢量信息的流形矩陣擴展成一個過完備的冗餘字典,它包含源的所有可能的位置信息,進而從冗餘的位置信息中提取所需的角度信息。隨著字典冗餘度的增大,計算量也急劇增加,為了減少計算量,本文採用奇異值分解(SVD)的方法進行處理。
下面結合附圖和具體實施方式進一步詳細說明本發明。
本發明提出了一種導向矢量失配情況下的基於稀疏表示的信號源DOA估計算法,具體的實施過程可以分為三個部分。
第一部分為信號模型的構建。
假設處於遠場環境下的Q個窄帶隨機信號源發射的信號波到達由P個傳感器組成的均勻線性陣列(ULA),其中這Q個信號源之間相互獨立,並且噪聲與信號互不相關。第q個信號源的到達角記為θq,在t時刻,第p個傳感器處的接收信號為式中,a(θq)為第q個信號源sq(t)在其波達方向θq上第p個傳感器處的導向矢量,表達式為d為傳感器之間的距離,λ為信號波長。gp為實際環境中第p個傳感器處的導向矢量增益值,sq(t)為空間中隨機分布的窄帶信號,np(t)為空間噪聲信號。
第二部分為基於分數低階矩的信號模型處理及增益值最優化估計。
本發明利用合成圓對稱廣義高斯噪聲對實際噪聲環境進行模擬,相對普通的噪聲分布其衰減速率更加緩慢,能夠更加真實地模擬實際環境噪聲分布,其概率密度函數(probability density function,PDF)表示為
式中,Γ(·)表示伽馬函數,α為穩定分布係數,σ為函數方差,並且當α=2時,噪聲呈現高斯分布。
在本發明中我們採用基於分數低階矩(FLOM)的方法對這種噪聲進行處理。均勻線性傳感器陣列的接收信號x(t)分數低階矩矩陣是一個P×P的矩陣,它的第(i,k)個分量為
式中,E(·)表示期望值,x*(t)表示其共軛函數,x(t)中各個信號之間互不相關,ε為小於α的指數參數。
將信號時域模型代入到傳感器陣列接收信號x(t)的分數低階矩矩陣表達式中
將Rik分解為兩部分Cik和Dik,其中
式中,為克羅內克符號,i,k為分數低階矩矩陣分量的下標,θq,θr分別為第q個和第r個信號源的到達角,sq(t),sr(t)分別為第q和第r個信號源的發射信號,且在上式中
因此,傳感器陣列的分數低階矩矩陣可表示為
R=GAΓAH+γI
式中,I為P×P階的單位矩陣,A為陣列流形矩陣,H表示共軛轉置。
將得到的傳感器陣列接收信號x(t)按照時間間隔T進行K次採樣得到採樣信號x(n),則可以得到其協方差矩陣的表達式
根據獲取到的採樣數據,我們可以利用加權最小二乘法得到增益函數,再通過求取增益函數的最小值來獲得無定向增益的最優解
式中,W是權重係數,通常情況下是未知的,但由於在淺海環境中,環境噪聲對信號處理的影響會比較大,因此這裡先利用W=Ι對其進行初始化,之後用對每次的採樣數據進行修改,則上式中的增益函數可改寫為
由於傳感器陣列是由P個傳感器組成的,則每個傳感器處的增益函數可記為
式中,wn=ζ(Wn)且z=ζp(GAΓAH)/gp,其中操作符ζp(·)表示從一個矩陣中選擇其第p列作為列向量,並去掉向量中第p個元素。
這樣最優增益值求解問題就轉化為求解P個線性最小二乘問題,然後對增益函數求最小值來求得最終結果,在這裡我們引入公式zw=z⊙wn,則求出的最優增益值為
第三部分為基於稀疏表示的DOA估計。
為了增加傳感器陣列可測得的信號源數目,對增益值優化後的分數低階矩矩陣進行矢量化
式中,vec表示矢量化運算,和⊙分別表示矩陣的Kronecker積和Khatri-Rao積。
則K個採樣幀內所有的分數低階矩矩陣矢量化後可得
式中,yk為每個採樣幀內的矢量化分數低階矩矩陣,定義我們可以看到由於響應矩陣矩陣Y的維數變為P2,大於通常所採用的物理維數P(P>1時),因此能夠使用少於目標源數目的傳感器對其進行測量,但可測得的信號源數目Q與陣元數P需滿足Q≤2(P-1)。
下面利用得到的矢量化FLOM矩陣採用基於稀疏表示的方法進行DOA估計。在得到矢量化的分數低階矩矩陣之後,採用稀疏表示方法對DOA角度進行冗餘化處理。稀疏表示DOA估計方法的主要思想是用角度集合覆蓋所有可能的目標信號入射方向,且滿足N>>Q,N是劃分的空間角度的個數,基於此可構成一個過完備的冗餘字典它包含源的所有可能的位置信息,進而採取某些方法從冗餘的位置信息中提取出所需的角度信息。隨著字典冗餘度的增大,計算量也急劇增加,為了減少計算量,本文採用奇異值分解(SVD)的方法對K幀內的矢量化分數低階矩矩陣進行處理。
式中,和分別為左奇異矩陣和右奇異矩陣,為對角陣。
可以得到信號子空間
式中,I為Q×Q階的單位矩陣,
因此,可以將信號源DOA求解問題轉化為
式中,||·||1和||·||2分別表示l1範數和l2範數,規則化參數β用來平衡信號稀疏性和噪聲的影響。
根據陣列輸出數據的有限快拍數我們只能得到的估計結果並且它們近似相等因此我們把上式的最優化問題轉化為
式中,參數λ用來平衡l1範數和l2範數,目標函數的前一項反映失配程度,後一項反映稀疏性要求。
上式是一個二階錐規劃問題,我們可以利用內點法進行求解,進而根據非零元素的位置求得信號源的DOA估計值,結果如圖2所示。
