基於變電站測試數據計算諧波阻抗和負荷諧波模型的方法與流程
2023-05-10 05:32:04 1
本發明涉及電力系統分析與計算技術領域,是一種基於變電站測試數據計算諧波阻抗和負荷諧波模型的方法。
背景技術:
在社會各個行業中電能的應用無處不在,電能生產和運輸管理顯得尤為重要。現有電網中包含有各種動態和靜態元件,形成了一個巨大的電力系統數學網絡,其結構複雜、階數高、強非線性、計算量巨大。為了拓展整個電力潮流的管理水平,建立基波之外的潮流模型描述是必不可少的步驟。目前,電力系統潮流網絡圖模型多是以下三種方式得到:1、採用典型參數,該種情況主要適用於動態元件的規劃期;2、設備廠家提供的參數,該種情況適用於靜態元件:線路、變壓器等參數;3、實測模型參數,該種情況主要適用於勵磁、PSS等動態元件。目前,還沒有一種利於實測的電能質量數據以建立簡化模型的方式能夠完成系統諧波網架的搭建。
技術實現要素:
本發明提供了一種基於變電站測試數據計算諧波阻抗和負荷諧波模型的方法,克服了上述現有技術之不足,其能有效解決電網中的動態和靜態元件形成的電網系統數學網絡結構複雜、階數高、強非線性、計算量巨大不易建立簡化模型的問題以及建立電網模型系統操作步驟繁雜,可靠性低,技術風險高的問題。
本發明的技術方案是通過以下措施來實現的:一種基於變電站測試數據計算諧波阻抗和負荷諧波模型的方法,包括以下步驟:
第一步:收集變壓器高壓側和低壓側的諧波數據,將關注時間段內的變壓器實測歷史數據導出得到諧波數據文件;
第二步:建立變壓器模型,根據諧波數據文件建立變壓器模型;
第三步:建立電網模型,利用疊加定理根據諧波數據文件和變壓器模型建立關於諧波源和負荷的模型;
第四步:建立簡化數學框架模型,將電網諧波網絡簡化為電網諧波阻抗模型、變壓器模型和負荷諧波模型三部分;
第五步:根據輸入量的概率分布和電網模型,求解得到電網諧波參數和負荷諧波參數;
第六步:根據電網諧波參數和負荷諧波參數並依據概率分布特性,計算得到電網諧波參數的特徵量和負荷諧波參數的特徵量;
第七步:建立諧波阻抗模型和負荷諧波模型並對諧波阻抗模型和負荷諧波模型仿真驗證。
下面是對上述發明技術方案的進一步優化或/和改進:
上述第一步中可通過電能質量在線檢測平臺或可攜式電能質量分析儀測得的實際數據推導得到諧波數據文件。
上述第三步中,建立電網模型時要收集並計算電網諧波和諧波負荷的數據,即配電線路的數據,線路、導線、配變設備、電纜和分段線路的基礎數據。
上述第四步中,建立簡化數學框架模型通過simulink軟體來搭建電網諧波阻抗模型和負荷諧波模型簡圖。
上述第七步中,通過MATLAB軟體對諧波阻抗模型和負荷諧波模型進行仿真驗證。
本發明基於實測電能質量數據,綜合二埠模型、線性疊加定律、概率統計規律理論,採用建立簡化模型的方式,完成諧波阻抗和負荷諧波阻抗的求解,並完成系統諧波網架的搭建,為電力系統諧波分布和擴散提供理論依據。相比於傳統的基於無功補償支路或者注入諧波電流的方法進行諧波阻抗估計,節省了系統操作的步驟,提供模型估計技術可靠性,降低了對應的操作技術風險,本發明更加有利於電網運行和生產部門對電網網架主體結構和用戶模型的分析和管理,準確分析和評估電網網架的諧波分布和流向。
附圖說明
附圖1為本發明實施例1的整體結構框圖。
附圖2為本發明實施例2的簡化電網模型圖。
附圖3為本發明實施例2的變壓器諧波模型圖。
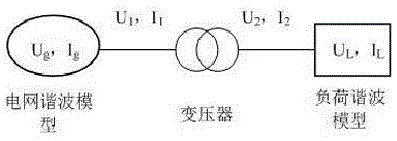
附圖4為本發明實施例2的帶有二埠模型的系統簡化模型圖。
具體實施方式
本發明不受下述實施例的限制,可根據本發明的技術方案與實際情況來確定具體的實施方式。
在本發明中,為了便於描述,各部件的相對位置關係的描述均是根據說明書附圖1的布圖方式來進行描述的,如:前、後、上、下、左、右等的位置關係是依據說明書附圖的布圖方向來確定的。
下面結合實施例及附圖對本發明作進一步描述:
實施例1:如附圖1所示,該基於變電站測試數據計算諧波阻抗和負荷諧波模型的方法包括以下步驟:
第一步:收集變壓器高壓側和低壓側的諧波數據,將關注時間段內的變壓器實測歷史數據導出得到諧波數據文件;
第二步:建立變壓器模型,根據諧波數據文件建立變壓器模型;
第三步:建立電網模型,利用疊加定理根據諧波數據文件和變壓器模型建立關於諧波源和負荷的模型;
第四步:建立簡化數學框架模型,將電網諧波網絡簡化為電網諧波阻抗模型、變壓器模型和負荷諧波模型三部分;
第五步:根據輸入量的概率分布和電網模型,求解得到電網諧波參數和負荷諧波參數;
第六步:根據電網諧波參數和負荷諧波參數並依據概率分布特性,計算得到電網諧波參數的特徵量和負荷諧波參數的特徵量;
第七步:建立諧波阻抗模型和負荷諧波模型並對諧波阻抗模型和負荷諧波模型仿真驗證。
這裡,第四步中電網諧波網絡為電網模型;根據需要,將電網模型進行簡化,能夠更直觀簡單的對變電站數據進行計算。
可根據實際需要,對上述基於變電站測試數據計算諧波阻抗和負荷諧波模型的方法作進一步優化或/和改進:
如附圖1所示,所述的第一步中,通過電能質量在線檢測平臺或可攜式電能質量分析儀測得的實際數據推導得到諧波數據文件。實際工作過程中可以將關注時間段內測的數據導出並以vdf或者pqdif格式的數據文件進行存儲;
如附圖1所示,所述的第三步中,建立電網模型時要收集並計算電網諧波和諧波負荷的數據,即配電線路的數據,線路、導線、配變設備、電纜和分段線路的基礎數據。實際工作過程中,在建立電網模型之前要考慮到電網背景諧波和諧波負荷對電網模型的影響。
如附圖1所示,所述的第四步中,建立簡化數學框架模型時通過simulink軟體來搭建電網諧波阻抗模型和負荷諧波模型簡圖。
如附圖1所示,所述的第七步中,通過MATLAB軟體對諧波阻抗模型和負荷諧波模型進行仿真驗證。
實施例2:如圖2、3、4所示,一種基於變電站測試數據計算諧波阻抗和負荷諧波模型的方法,包括以下步驟:
第一步:建立簡化電網模型,包括變壓器模型、電網諧波阻抗模型、負荷諧波模型。電網側簡化為諧波源模型,對於電流型負荷,負荷側簡化為電流源模型;對於電壓型負荷,負荷側簡化為電壓源模型。這裡推導是電流源型模型;
第二步:建立變壓器模型,根據二埠模型,簡化計算公式如下:
其中:U1、I1為變壓器一次側電壓和電流,U2、I2為變壓器二次側電壓和電流。Y=1/Z(h)。變壓器為無源網絡,阻抗矩陣具有對稱特性,所以z12=z21;
第三步:.求解變壓器參數,變壓器參數通過式(1)得到,計算公式如下:
Yy=
(3);
第四步:變壓器側測量數據的概率分布,假設U1和I1符合高斯分布,且相互獨立;則根據式(1)可以得出:
其中:Z1和Z2是U1和I1標準化之後的相互獨立的標準正態分布。
根據式(4)可得出U1和I1、U2、I2符合四元聯合高斯分布,對應得分布函數為:
其中∑X為方差矩陣,(X-μ)是均值向量;
第五步:利用疊加原理,根據附圖3可以得到待求變量和測量變量之間的代數關係為:
第六步:求解電網諧波阻抗模型和負荷諧波模型的概率密度,根據概率密度函數的性質,列出Ug、Zg、ZL、IL關於U1、I1、U2、I2的雅克比矩陣為:
根據式(10),Ug、Zg、ZL、IL的聯合概率密度函數為:
f(Ug,Zg,ZL,IL)=f(U1,I1,U2,I2)|J|-1;
(11)
第七步:電網諧波阻抗模型和負荷諧波模型的概率特徵值求解,根據式(11)可以求解得出Ug、Zg、ZL、IL的邊緣概率密度函數:
f(Ug)=∫∫∫R3f(Ug,Zg,ZL,IL)dZgdZLdIL
(12)
f(Zg)=∫∫∫R3f(Ug,Zg,ZL,IL)dUgdZLdIL
(13)
f(ZL)=∫∫∫R3f(Ug,Zg,ZL,IL)dUgdZgdIL
(14)
f(IL)=∫∫∫R3f(Ug,Zg,ZL,IL)dUgdZgdZL
(15)
根據式(12)-(15)可以得出Ug、Zg、ZL、IL的期望和方差、95%概率值:
其他三個變量的統計特徵量求解方法與公式(16)、(17)相同,這裡不再贅述。
如附圖2、3、4所示,在第四步中,變壓器測試數據的概率分布確定有多種方法,可以用貝葉斯估計或者直接假設符合某種分布,調用統計軟體函數判斷是否符合某種特定的概率分布。這裡舉例為為高斯分布,僅為說明該方法的實現步驟,並不代表變壓器的測試數據傾向於高斯分布。
以上技術特徵構成了本發明的實施例,其具有較強的適應性和實施效果,可根據實際需要增減非必要的技術特徵,來滿足不同情況的需求。
