最優反應動態演化博弈模型的網絡防禦策略選取方法與流程

2023-08-05 14:35:41 5

本發明屬於計算機網絡安全防禦技術領域，具體的涉及一種最優反應動態演化博弈模型的網絡防禦策略選取方法。

背景技術：

近年來，網際網路的迅猛發展給人們的社會生活帶來了巨大的變化，特別是「網際網路+」戰略將網際網路的發展推向一個新的高潮。隨著網際網路的快速發展，網絡空間安全問題也日益突出。網絡安全問題已經非常嚴峻，針對境內外的各類網絡攻擊行為，如何加強網絡安全防禦成為當今時代亟需解決的問題，亟需能夠對網絡攻防行為進行分析和預測，進而實施主動安全防禦的新技術。由於網絡安全狀態在本質上由攻防雙方的對抗行為及其結果決定，並且網絡攻防對抗中所具有的目標對立性、策略依存性和關係非合作性正是博弈論的基本特徵，因此博弈論在網絡安全領域的研究和應用日漸興起，並且以採用經典傳統博弈模型對網絡安全行為進行分析為主。

但是，已有研究成果大都以傳統博弈理論為基礎，建立在參與者完全理性假設的前提下，而這樣的假設與實際情況並不相符。其博弈模型與現實偏差較大，從而降低了安全防禦策略選取方法的準確性和指導意義。針對以上問題，部分學者以有限理性為前提，採用演化博弈論應用於網絡攻防分析。通過分析，演化博弈更加符合網絡攻防對抗動態演化的現實，將攻防雙方的行為模型化為具有某種適應性學習能力的漸進演化過程，採用典型的複製動態方程進行求解與分析。但複製動態學習機制存在學習速度慢、策略選取效率低等問題。

技術實現要素：

本發明針對現有研究成果大都以傳統博弈理論為基礎，建立在參與者完全理性假設的前提下，而這樣的假設與實際情況並不相符，存在若將其直接應用於網絡攻防對抗演化博弈分析，將會存在學習周期過長、學習效率不高，這將很大程度上降低模型和方法的適用性問題，提出一種最優反應動態演化博弈模型的網絡防禦策略選取方法。

本發明的技術方案是：一種最優反應動態演化博弈模型的網絡防禦策略選取方法，包括以下步驟：

步驟1：基於有限理性條件，利用最優反應動態學習機制，構建基於最優反應動態的攻防演化博弈模型；

步驟2：利用防禦方策略選取動態演化過程及防禦演化均衡點，對不同防禦者之間防禦策略選取問題進行了研究；

步驟3：在建立的最優反應動態演化博弈模型基礎上，通過具體的算例對該模型進行分析與求解，推廣演化博弈模型。

所述的最優反應動態演化博弈模型的網絡防禦策略選取方法，所述步驟1中最優反應動態演化博弈模型可表示為四元組，brdegm＝(d,ds,p,u)

d＝{d1,d2,…dn}表示防禦參與者空間，其中，di表示防禦者i，不同的防禦者可以選取不同的防禦策略；

ds＝{ds1,ds2,…dsm}表示防禦者策略空間，不同的防禦者共同享有該防禦策略集；

p＝{p1,p2,…pm}表示防禦者信念集合，其中，pi表示防禦者選取防禦策略dsi的概率；

u＝{u1,u2,…um}表示收益函數集合，其中，ui表示防禦者選取防禦策略dsi所獲取的收益。

所述的最優反應動態演化博弈模型的網絡防禦策略選取方法，所述最優反應動態方程為其中nt表示n個防禦者中選取策略ds1的個數，ds1是可選策略集中的任意一個防禦策略。

所述的最優反應動態演化博弈模型的網絡防禦策略選取方法，所述步驟2中防禦方策略選取動態演化過程為：在網絡攻防對抗過程中，不同防禦策略之間存在一種競爭關係，高收益的防禦策略將會淘汰掉收益較低的策略。

所述的最優反應動態演化博弈模型的網絡防禦策略選取方法，所述高收益的防禦策略將會淘汰掉收益較低的策略中，收益矩陣為：其中，u1、u2分別為策略ds1、ds2的收益，a為u1、u2的差值。

所述的最優反應動態演化博弈模型的網絡防禦策略選取方法，所述步驟3中推廣演化博弈模型主要為，當防禦方存在任意n個防禦者時，基於最優反應動態演化博弈模型，對任意兩個防禦策略dsi和dsj進行演化博弈分析，假設dsi是相對於dsj的優勢策略，且i≠j，隨著時間的推移，最終得到一定的演化規律。

所述的最優反應動態演化博弈模型的網絡防禦策略選取方法，所述演化規律為：對於存在n個防禦者的防禦方，當所有防禦者在初次博弈中都選取防禦策略dsi或者策略dsj時，採用最優反應動態學習機制，整個網絡防禦方的策略選取最終達到的穩定狀態則為所有的防禦者均選取策略dsi或者策略dsj。

所述的最優反應動態演化博弈模型的網絡防禦策略選取方法，所述演化規律為：對於存在n個防禦者的防禦方，當n為奇數時，在初次博弈中，只要有一個防禦者選取了策略dsi，通過最優反應動態學習機制對自身策略經過多個時期的反覆調整，最終都會收斂於所有防禦者選取策略dsi的穩定狀態。

所述的最優反應動態演化博弈模型的網絡防禦策略選取方法，所述演化規律為：對於存在n個防禦者的防禦方，當n為偶數時，在初次博弈中，有一個防禦者選取了防禦策略dsi，其他防禦者均選取策略dsj，那麼，最優反應動態無法使所有防禦者收斂於某個穩定狀態，隨著時間的演化，各防禦者對策略的調整隻能陷入周期循環變動。

所述的最優反應動態演化博弈模型的網絡防禦策略選取方法，所述演化規律為：對於存在n個防禦者的防禦方，在初次博弈中，只要存在兩個相鄰防禦者同時選取了策略dsi，在最優反應動態學習機制下，隨著時間的演化，最終會收斂於所有防禦者全部選取策略dsi的穩定狀態。

本發明的有益效果是：本發明建立了有限理性條件下的非合作網絡攻防演化博弈模型，並對該模型進行了均衡分析與求解。在此基礎上，從防禦者角度出發，針對不同防禦者之間的策略學習調整過程，採用最優反應動態學習機制，建立了防禦者之間的多階段重複動態演化博弈模型，對不同防禦者之間防禦策略選取問題進行了研究。在建立的最優反應動態演化博弈模型基礎上，通過具體的算例對該模型進行了分析與求解，並將該模型作進一步推廣，提高了模型的通用性。針對防禦者個數奇偶性的不同，以及防禦方策略選取初始狀態的不同，都會影響整個博弈系統的最終演化結果。通過安排防禦方策略選取初始狀態，經過不斷演化，最優反應動態最終將會使博弈系統達到某個穩定狀態，從而得到最優防禦策略。說明本發明提出的方法能夠很好的應用於網絡安全防禦策略選取問題，對網絡安全研究能夠提供一定的指導意義。

附圖說明

圖1本發明的方法步驟示意框圖；

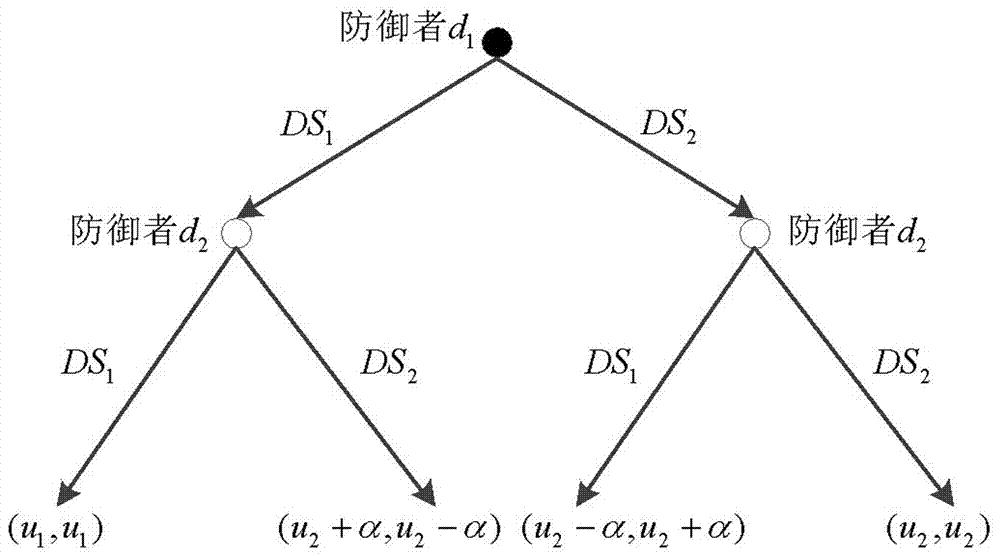
圖2網絡防禦者博弈樹示意圖；

圖3初次博弈1個ds1的最優反應動態示意圖；

圖4初次博弈兩個ds1的最優反應動態策略調整過程示意圖；

圖5初次博弈三個ds1的最優反應動態策略調整過程示意圖；

圖6當n為奇數，初始狀態只有一個選ds1仿真效果示意圖；

圖7當n為奇數，初始狀態存在兩個相鄰防禦者選ds1仿真效果示意圖。

具體實施方式

實施例1，結合圖1-圖7，一種最優反應動態演化博弈模型的網絡防禦策略選取方法，包括以下步驟：

步驟1：基於有限理性條件，利用最優反應動態學習機制，構建基於最優反應動態的攻防演化博弈模型；

步驟1中最優反應動態演化博弈模型可表示為四元組，brdegm＝(d,ds,p,u)

d＝{d1,d2,…dn}表示防禦參與者空間，其中，di表示防禦者i，不同的防禦者可以選取不同的防禦策略；

ds＝{ds1,ds2,…dsm}表示防禦者策略空間，不同的防禦者共同享有該防禦策略集；

p＝{p1,p2,…pm}表示防禦者信念集合，其中，pi表示防禦者選取防禦策略dsi的概率；

u＝{u1,u2,…um}表示收益函數集合，其中，ui表示防禦者選取防禦策略dsi所獲取的收益。

最優反應動態方程為其中nt表示n個防禦者中選取策略ds1的個數，ds1是可選策略集中的任意一個防禦策略。

步驟2：利用防禦方策略選取動態演化過程及防禦演化均衡點，對不同防禦者之間防禦策略選取問題進行了研究；

步驟2中防禦方策略選取動態演化過程為：在網絡攻防對抗過程中，不同防禦策略之間存在一種競爭關係，高收益的防禦策略將會淘汰掉收益較低的策略；高收益的防禦策略將會淘汰掉收益較低的策略中，收益矩陣為：其中，u1、u2分別為策略ds1、ds2的收益，a為u1、u2的差值。

步驟3：在建立的最優反應動態演化博弈模型基礎上，通過具體的算例對該模型進行分析與求解，推廣演化博弈模型。

步驟3中推廣演化博弈模型主要為，當防禦方存在任意n個防禦者時，基於最優反應動態演化博弈模型，對任意兩個防禦策略dsi和dsj進行演化博弈分析，假設dsi是相對於dsj的優勢策略，且i≠j，隨著時間的推移，最終得到一定的演化規律。

進一步的：演化規律為：對於存在n個防禦者的防禦方，當所有防禦者在初次博弈中都選取防禦策略dsi或者策略dsj時，採用最優反應動態學習機制，整個網絡防禦方的策略選取最終達到的穩定狀態則為所有的防禦者均選取策略dsi或者策略dsj。

進一步的，演化規律為：對於存在n個防禦者的防禦方，當n為奇數時，在初次博弈中，只要有一個防禦者選取了策略dsi，通過最優反應動態學習機制對自身策略經過多個時期的反覆調整，最終都會收斂於所有防禦者選取策略dsi的穩定狀態。

進一步的，演化規律為：對於存在n個防禦者的防禦方，當n為偶數時，在初次博弈中，有一個防禦者選取了防禦策略dsi，其他防禦者均選取策略dsj，那麼，最優反應動態無法使所有防禦者收斂於某個穩定狀態，隨著時間的演化，各防禦者對策略的調整隻能陷入周期循環變動。

進一步的，演化規律為：對於存在n個防禦者的防禦方，在初次博弈中，只要存在兩個相鄰防禦者同時選取了策略dsi，在最優反應動態學習機制下，隨著時間的演化，最終會收斂於所有防禦者全部選取策略dsi的穩定狀態。

實施例2，結合圖1-圖7，一種最優反應動態演化博弈模型的網絡防禦策略選取方法，用於分析網絡攻防演化博弈過程。由於常用的複製動態學習機制存在學習速度較慢，學習效率不高等問題，本發明仍然採用演化博弈的思想，基於有限理性條件，利用最優反應動態學習機制，構建基於最優反應動態的攻防演化博弈模型，分析防禦方策略選取動態演化過程及防禦演化均衡點，對不同防禦者之間防禦策略選取問題進行了研究。在建立的最優反應動態演化博弈模型基礎上，通過具體的算例對該模型進行了分析與求解，並將該模型作進一步推廣，提高了模型的通用性。本發明提出的方法能夠很好的應用於網絡安全防禦策略選取問題，對網絡安全研究能夠提供一定的指導意義。

在網絡攻防博弈系統中，決策者通過不斷試錯、模仿和策略調整，從初始狀態隨著時間不斷演化，最終能夠達到某個演化穩定均衡，而決策者的策略學習方法及過程直接影響到最終的演化穩定狀態。針對防禦方，假設不同的防禦者共享同一個防禦策略集。由於不同的防禦策略會給防禦者帶來不同的收益，在收益差異的牽引和學習機制的驅動下，低收益防禦者不斷學習收益高的防禦者的策略。隨著時間的演化，低收益的策略將會被高收益的策略所淘汰。針對現實的網絡攻擊行為，從防禦方角度出發，根據不同防禦者之間的協同關係，將最優反應動態學習機制運用於不同防禦策略之間的博弈，建立多階段最優反應動態重複演化博弈模型。在上述「學習—改進」機制的推動下，不同防禦策略的選取概率呈現動態演化趨勢，最終可以分析得到網絡安全防禦策略選取方法。

最優反應動態演化博弈模型

針對網絡防禦方，以演化博弈理論為基礎，在有限理性的條件下，採用最優反應動態快速學習機制，構建不同防禦者之間的最優反應動態演化博弈模型。

定義1最優反應動態演化博弈模型brdegm(best-responsedynamicsevolutionarygamemodel)可以表示為四元組，brdegm＝(d,ds,p,u)，其中

①d＝{d1,d2,…dn}表示防禦參與者空間。其中，di表示防禦者i，不同的防禦者可以選取不同的防禦策略。

②ds＝{ds1,ds2,…dsm}表示防禦者策略空間。不同的防禦者共同享有該防禦策略集。

③p＝{p1,p2,…pm}表示防禦者信念集合。其中，pi表示防禦者選取防禦策略dsi的概率。

④u＝{u1,u2,…um}表示收益函數集合。其中，ui表示防禦者選取防禦策略dsi所獲取的收益。

在網絡攻防對抗過程中，不同防禦策略之間存在一種競爭關係，高收益的防禦策略將會淘汰掉收益較低的策略。針對任意兩個防禦者d1和d2，假設ds1、ds2是可選策略集中的任意兩個防禦策略，其中ds1是相較ds2的優勢策略，即策略ds1比ds2有更好的防禦效果，會帶來更高的防禦收益，但ds1所對應的防禦成本比ds2高。採用最優反應動態快速學習機制，建立有限理性條件下的演化博弈模型。博弈樹如圖2所示。

當博弈雙方分別選取策略ds1和ds2時，選取ds1將獲取更高的防禦收益，記成本高出部分為α，此時，選取策略ds1的防禦者獲得收益u2-α，而選取策略ds2的防禦者因為搭便車等行為則獲取了更高的收益，記為u2+a。其中，u1-u2＞＞a。

從得益矩陣可以看出，該博弈中存在兩個純策略納什均衡(ds1,ds1)和(ds2,ds2)，其中(ds1,ds1)是帕累託上策均衡。但是如果還要考慮防禦者之間的信任關係，或者對風險敏感性等因素，則均衡(ds2,ds2)出現的可能性會更大。

基於以上博弈條件，假設所有的防禦者都處於一個圓周之上，每個防禦者與各自的左右鄰居進行重複博弈，學習比自身策略收益高的防禦策略。記博弈雙方所獲的收益分別為∏1和∏2，設pi(t)為在t時期，博弈者i的鄰居中選取策略ds1的數量，該數量可能的取值有0、1、2三種情況。由此可得，博弈者選取策略ds1時所獲收益為∏1＝u1×pi(t)+(u2-a)×[2-pi(t)]，選取策略ds2時所獲收益為∏2＝(u2-a)×pi(t)+u2×[2-pi(t)]。根據最優反應動態機制可知，當∏1>∏2，即時，博弈者將在下一博弈階段選取策略ds2。由此可以得到以下最優反應動態方程。

其中，nt表示n個防禦者中選取策略ds1的個數。通過該博弈動態方程可知，網絡防禦策略選取的最終穩定狀態將是對於防禦策略選取的某種趨勢。

演化博弈模型分析與求解

基於以上建立的最優反應動態演化博弈模型，對防禦者之間的策略學習過程進行詳細的描述與分析。在網絡攻防對抗中，由於防禦者都是有限理性的，並且具有快速學習的能力，能夠對上一階段的博弈結果進行分析總結，並立刻做出相應的策略調整，實現下一階段的防禦收益最大化。隨著時間的推移，整個防禦方的策略選取將會達到一個穩定的狀態。

下面將採用從特殊到一般的思路，採用最優反應動態學習機制，對圓周博弈進行具體分析。

假設防禦方具有5個防禦者，且5個防禦者分布於圓周上5個不同的位置，如圖3所示，每個位置上的防禦者既可以選取策略ds1，也可以選取策略ds2，因此，該博弈具有32個初始狀態，其中包括一個全部選取策略ds1，一個全部選取策略ds2，剩下30個均包含ds1和ds2兩種策略。

pi(t)為在t時期，博弈者i的鄰居中選取策略ds1的數量，該數量可能的取值有0、1、2三種情況。相應地，選取策略ds2的鄰居數量為1-pi(t)，同樣存在0、1、2三種取值。根據最優反應動態機制可知，當∏1>∏2，即時，博弈者將在下一博弈階段選取策略ds2。已知u1-u2＞＞α，則由於pi(t)只存在0、1、2三種取值，如果在t時期博弈者i的兩個鄰居中只要有一個選取了策略ds1，則博弈者i在t+1時期就會選取ds1策略；如果兩個鄰居都沒有選取策略ds1，則博弈者i在t+1時期就會選取ds2策略。由此可以得出，當5個防禦者初次全部選取ds1策略(ds2策略)時，最終的穩定狀態為所有防禦者均選取ds1策略(ds2策略)。

如果在初次博弈中有1個防禦者選取了ds1策略，而其他防禦者均採用ds2策略的時，那麼這5個防禦者經過4個時期的反覆策略調整，最終收斂到了所有防禦者都採用ds1策略的穩定狀態。如圖3所示，對於給定防禦方的初始狀態(ds1,ds2,ds2,ds2,ds2)，經過4次的階段演化，防禦方最終達到了穩定狀態(ds1,ds1,ds1,ds1,ds1)。

由圖3中的最優反應動態調整過程可以看出，已經包含了有兩個不相鄰防禦者採用ds1、三個非相鄰博弈者採用ds1、四個防禦者採用ds1這幾種初次博弈情況的最優反應動態調整過程，它們分別需要三個、兩個和一個階段的調整即可達到全部採用ds1策略的穩定狀態。下面對初次博弈中有兩個非相鄰防禦者和三個相鄰防禦者採用ds1的情況進行分析。

由圖4可知，兩個相鄰防禦者採用ds1的最優反應動態策略調整過程只需兩個階段即可達到所有防禦者選取ds1策略的穩定狀態。由圖5可知，三個相鄰防禦者採用ds1的最優反應動態策略調整過程只需一個階段即可達到所有防禦者選取ds1策略的穩定狀態。

由以上分析可知，32種可能的初次博弈情況中，只有一種是演化穩定於所有防禦者選取策略ds2，其餘31種最終都會收斂於全部選取ds1的狀態。說明所有防禦者選取策略ds1或ds2屬於該博弈過程中的穩定狀態，但收斂於ds1的概率要遠遠大於ds2。

進一步理解上述兩個演化穩定狀態，如果防禦方在達到所有防禦者選取策略ds1的穩定狀態下，出現少數防禦者偏離策略ds1的情況，最優反應動態會使防禦者的策略很快收斂到都選取ds1的狀態。因此，所有防禦者都選取ds1的穩定狀態是具有穩定性的。相反，當達到所有防禦者選取ds2的穩定狀態卻不是穩健的，因為一旦某個防禦者偏離ds2，最優反應動態會使防禦方的狀態離該穩定狀態越來越遠，因此該均衡並不是真正穩定的。隨著長時間的演化，防禦者最終將都會選取策略ds1。

演化博弈模型的推廣

由於在實際的網絡防禦過程中，防禦方由多個防禦者構成，因此必須對該博弈模型作進一步推廣，即當防禦方存在任意n個防禦者時，基於以上快速反應動態演化博弈模型，對任意兩個防禦策略dsi和dsj進行演化博弈分析(假設dsi是相對於dsj的優勢策略，且i≠j)，隨著時間的推移，最終得到一定的演化規律。針對以上特定數目網絡防禦者的演化博弈分析，通過進一步分析總結，可以得到以下命題。

命題1：對於存在n個防禦者的防禦方，當所有防禦者在初次博弈中都選取防禦策略dsi(策略dsj)時，採用最優反應動態學習機制，整個網絡防禦方的策略選取最終達到的穩定狀態則為所有的防禦者均選取策略dsi(策略dsj)。

命題2：對於存在n個防禦者的防禦方，當n為奇數時，在初次博弈中，只要有一個防禦者選取了策略dsi，通過最優反應動態學習機制對自身策略經過多個時期的反覆調整，最終都會收斂於所有防禦者選取策略dsi的穩定狀態。

命題3：對於存在n個防禦者的防禦方，當n為偶數時，在初次博弈中，有一個防禦者選取了防禦策略dsi，其他防禦者均選取策略dsj，那麼，最優反應動態無法使所有防禦者收斂於某個穩定狀態，隨著時間的演化，各防禦者對策略的調整隻能陷入周期循環變動。

命題4：對於存在n個防禦者的防禦方，在初次博弈中，只要存在兩個相鄰防禦者同時選取了策略dsi，在最優反應動態學習機制下，隨著時間的演化，最終會收斂於所有防禦者全部選取策略dsi的穩定狀態。

命題5：對於存在n個防禦者的防禦方，如果通過安排防禦者在初次博弈中的策略，經過不斷的動態演化，使得該博弈系統到達某一階段時，出現了上述四個命題中的某個情形，後期將會出現同樣的演化過程。

數值仿真

基於以上建立的網絡攻防演化博弈，利用系統動力學進行實驗仿真，驗證網絡攻防演化博弈模型和最優反應動態演化博弈模型的有效性與合理性。防禦方選取不同的防禦初始狀態，整個博弈系統將會產生不同的演化結果。下面將針對防禦方的不同防禦初始狀態，進行具體的數值仿真。本發明將以命題2和命題4作為仿真對象。

(1)當n為奇數，且防禦方初始狀態為只有一個防禦者選取策略ds1，其他防禦者均選取策略ds2時，取n＝21，則選取策略ds1的防禦者所佔比例為選取策略ds2的防禦者所佔比例為此時，該博弈系統中防禦者之間存在調整改變自身策略的動力。通過系統仿真，發現防禦方選取策略ds1的防禦者比例成線性增長，而選取策略的ds2防禦者比例成線性減少，且在第10次仿真結果中就已經達到了最終的演化穩定狀態。具體如圖6所示。該演化結果可以是系統穩定狀態中的一種，此時ds1為最優防禦策略。

(2)當n為奇數，且防禦方初始狀態中存在兩個相鄰防禦者同時選取策略ds1，其他防禦者均選取策略ds2時，取n＝21，則選取策略ds1的防禦者所佔比例為選取策略ds2的防禦者所佔比例為此時，該博弈系統中防禦者之間存在調整改變自身策略的動力。通過不斷演化，防禦方選取策略ds1的防禦者比例成線性增長，而選取策略的ds2防禦者比例成線性減少，且在第10次仿真結果中達到最終演化穩定狀態。具體如圖7所示。該演化結果可以是系統穩定狀態中的一種，此時ds1為最優防禦策略。

根據以上仿真結果可知，針對防禦者個數奇偶性的不同，以及防禦方策略選取初始狀態的不同，都會影響整個博弈系統的最終演化結果。通過安排防禦方策略選取初始狀態，經過不斷演化，最優反應動態最終將會使博弈系統達到某個穩定狀態。將實驗結果與本文模型推理進行對比，可以看出實驗系統中的演化結果與文中的理論分析保持一致，說明該演化博弈模型符合現實系統演化規律，從而驗證了本模型的現實有效性。可以將其應用於現實的網絡攻防對抗中，對防禦方的聯合防禦進行具體分析與預測，為防禦方的策略選取提供有力的支撐。