基站額定功率固定的下行OFDMA系統的高能效資源分配方法與流程

2023-08-10 19:41:01

本發明涉及一種基站額定功率固定的下行OFDMA系統的高能效資源分配方法。

背景技術：

作為4G通信的重要技術之一，在移動通信領域還有巨大的發展前景。基站作為通信信號的發送端，在向移動終端發送信號時往往消耗巨大的能源。由耗能過多帶來的諸多問題也迫使人們逐漸關注能源的節約問題。如何在保證用戶通信速率和質量的同時，還能在基站端節約能源是大家關注的焦點之一。

能效指的是傳輸一比特數據所消耗的焦耳數。近些年很多人從數據傳輸速率的角度切入，期望找到實現高能效的解決方法。但是，這種方法往往對通信速率會產生較大的影響。於是，從基站發射信號功率的方向考慮能效節約問題，逐漸成為當下的熱點。

技術實現要素：

本發明的目的是提供一種基站額定功率固定的下行OFDMA系統的高能效資源分配方法。

為達到上述目的，本發明採用以下技術方案：

一種基站額定功率固定的下行OFDMA系統的高能效資源分配方法，包括以下步驟：

(1)根據能效的定義，確定優化問題(P1)的目標函數和約束條件：

目標函數：

其中，且

約束條件：

f(P)≤Pt；

其中，B為基站發射OFDM信號的帶寬，K為發射的子載波數，hu,k(k＝1,...,K,u＝1,...,U)為從基站到用戶的子載波的基帶信道係數，ξs(ξs＜1)為基站的功率放大器的效率，Pc為基站和所有用戶的總電路功率，σ2(Watt)為每個用戶接收機所對應的每個子載波的噪聲功率，Pk為基站發射OFDM信號的第k個子載波的平均功率，Pt為基站的額定總功率， P表示各子載波的功率分配集合，I表示子載波分配給用戶的情況；

(2)假設優化問題(P1)的約束條件中，基站的總功率消耗是固定值ρ，那麼將優化問題(P1)轉化成優化問題(P2)：

目標函數：

約束條件：f(P)＝ρ

由下式決定

這裡Gk＝maxu{Gu,k}

(3)步驟(2)中確定了一種最優的子載波分配方式，並結合步驟(1)中R(I,P)的表達式將優化問題(P2)進一步轉化成優化問題(P3)：

目標函數：

約束條件：f(P)＝ρ

利用凸優化理論中的KKT條件求解優化問題(P3)，得到子載波的功率分配為 其中，υ∈R是對等式約束條件f(P)＝ρ引入的拉格朗日乘子；

(4)結合條件∑kPk(ρ)＝ξs(ρ-Pc)，利用二分法求數值解的方法，得到 v*＝μ(ρ)以及是關於ρ的函數；

(5)利用二分法找到基站最佳能效的實際總功率ρ*。具體過程如下：

經證明，在ρ＞Pc時，是單調增的嚴格凹的函數，同時滿足從而得到，

按照以上條件，在同一坐標系中繪製η(ρ)以及μ(ρ)的圖像。

發現存在一個功率點ρ0，ρ從Pc增加到ρ0時，μ(ρ)是嚴格遞減的，η(ρ)是嚴格遞增的，且μ(ρ)＞η(ρ)(即)一直成立。

當ρ＝ρ0時，兩條直線重合，μ(ρ0)＝η(ρ0)(即)成立。

當ρ大於ρ0且單調遞增時，μ(ρ)和η(ρ)都是嚴格遞減的，且μ(ρ)＜η(ρ)(即)一直成立。

ρ*＝ρ0是使基站能效達到最優的實際總功率。

與現有技術相比，本發明具有如下的優點：

本發明方法對大功率OFDM信號發射基站的能源節約效果十分明顯，並且具有低複雜度的特點。

附圖說明

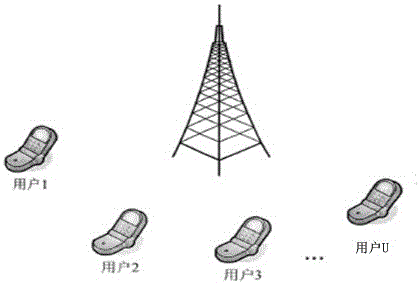
圖1為本發明的下行OFDMA系統模型。

圖2為本發明進行最大能效功率分配時，基站總功率ρ與能效函數η(ρ)、能效最優的數據傳輸率函數和能效最優的拉格朗日變量μ(ρ)的函數圖像。

圖3為本發明的方法流程圖。

具體實施方式

下面結合附圖和具體實施例對本發明作更進一步的說明。

如圖1所示，小區基站向該小區的U個用戶發射OFDM信號。基站的額定總功率為Pt。信號的總帶寬為B Hz，有K個子載波，每個子載波只分配給一個用戶。從基站到用戶u的子載波k的基帶信道係數為hu,k(k＝1,...,K,u＝1,...,U)。基站的功率放大器的效率為ξs(ξs＜1)。 基站和所有用戶的總電路功率為Pc(不包括基站功率放大器的功率)。每個用戶接收機所對應的每個子載波的噪聲功率為σ2(Watt)。

同時，定義變量Pk≥0表示從基站到子載波k符號傳輸的平均功率。而且變量tku∈{0,1}，當tku＝1時，子載波k被分配給用戶u，當tku＝0時，子載波k未被分配給用戶u。由此可知，下行鏈路OFDMA系統的高能效資源分配的優化變量為其中P表示各子載波的功率分配集合，I表示子載波分配給用戶的情況。

系統能效的衡量標準是消耗每焦耳能量所傳輸的比特數，因此需要求出基站發射信號時的總功率和數據傳輸率。

總功率包括電路功率Pc和發射功率PT，其具體表達式如下：

根據香農公式，基站到所有用戶的數據傳輸率為：

其中那麼在已知的情況下，就可以執行一個算法找到基站總功率固定時達到最大能效的最佳資源分配。

假設基站的總功率消耗限制在規定的有效值Pt(Pt＞Pc)以下。最大能效資源分配問題可以建立為優化問題(P1)：

約束條件為：

f(P)≤Pt；

本實施例分為兩部分來解決以上能效優化問題。步驟1進行子載波的最優分配，步驟2進行基站發射信號的功率最佳分配。

步驟1進行子載波的最優分配方法如下。

假設系統的總功率消耗是固定值ρ，那麼優化問題(P1)可以轉變為高頻譜效率的資源分配問題(P2)：

約束條件為：

式(3)，(4)，(5)，f(P)＝ρ；

則由下式決定

這裡，Gk＝maxu{Gu,k}。

式(6)的實際意義是，基站發射出來的每個子載波分配給信道最強的用戶，即規定了一種最優的子載波分配方式。分配方式要根據小區的具體環境而決定。

在子載波達到最佳分配後，接下來的問題就是找到能使基站能效最大化的功率分配方式。總功率消耗為ρ時，最大能效表達式為：

這裡，

此時，找到問題(P1)的最佳資源分配等同於先找到

然後I*和P*(ρ*)即為(P1)的最優解。

步驟2進行基站發射信號的功率最佳分配方法如下。

綜合問題(P1)、(P2)以及式(8)，得到求解P*(ρ)的最優化問題(P3)：

約束條件為：

式(5)，f(P)＝ρ

步驟201：對於問題(P3)可以利用凸問題的KKT條件進行求解。

對不等式約束(5)引入拉格朗日乘子λ∈Rn，對等式約束條件f(P)＝ρ引入一個乘子υ∈R，得到優化問題(P3)的拉格朗日函數為：

然後利用KKT條件來求解該優化問題。Pk*,(λ*,v*)分別是滿足原函數和對偶問題的最優解，同時，滿足如下的KKT條件：

分析求解得到：

可以表示為：

步驟202：通過式(13)可以看出，Pk無法用一個確定的解析式表達出來，但是可以確定它是一個關於υ的減函數，而且滿足∑kPk(ρ)＝ξs(ρ-Pc)。因此，利用二分法的思想求出當基站的總功率ρ給定一個值時，所對應的υ的具體數值，進而得到η(ρ)的數值解。步驟203：η(ρ)以及最優拉格朗日變量υ*的數值都與ρ相關。下面要對這三個函數的性質以及它們之間的相互關係進行分析，進而找到使能效函數η(ρ)達到最大時，基站發射信 號的實際功率ρ*。

假設v＝μ(ρ)，根據凸優化理論，可以得到：

同時還可以證明是關於ρ的遞增的嚴格的凹函數。根據的性質可以近似的畫出隨著ρ變化的曲線，如圖2。圖中的粗實線表示的是：時，的圖像。那麼η(ρ)函數圖像(虛線)的含義為原點和之間的連線，μ(ρ)函數圖像(點劃線)的含義為 在的切線。

對η(ρ)求關於ρ的導數：

結合圖2分析可知，ρ從Pc增加到ρ0時，η(ρ)是嚴格遞增的，且μ(ρ)＞η(ρ)一直成立。當ρ＝ρ0時，兩條直線重合，μ(ρ0)＝η(ρ0)成立。當ρ大於ρ0時，η(ρ)都是嚴格遞減的，且μ(ρ)＜η(ρ)一直成立。

我們發現ρ*＝ρ0時，使ρ0為最佳總功率的分配點。可以利用二分法來找到ρ*，這個過程實際上是比較μ(ρ)和η(ρ)大小關係的過程，當二者相等或者近似相等的時候，即為能效最優化的功率。

如圖3所示，給出了整個下行OFDMA系統的高能效資源分配算法的流程圖。本算法的核心部分在於通過觀察證明μ(ρ)和η(ρ)之間的關係，利用二分法找到高能效的功率分配方式。在最壞的情況下，它的算法複雜度為