一種計算空載高壓電力電纜最高承受電壓位置的方法與流程
2023-05-29 11:08:51
本發明涉及一種計算空載高壓電力電纜最高承受電壓位置的方法,屬於電力技術領域。
背景技術:
目前對於長距離輸電線路,正弦波電壓沿輸電線路電壓的計算多採用穩態分布參數電路推導的方法,計算線路的衰減係數和相位係數,從而計算出沿線各點的穩態電壓,但是無法解決正弦行波在輸電線路上瞬態電壓的計算問題。對於正弦行波沿電纜輸電線路,目前還沒有關於誤操作和故障等引起的正弦行波在長距離電纜輸電線路中沿線各點的最高承受的瞬態電壓的計算方法。
技術實現要素:
為了解決上述技術問題,本發明提供了一種計算空載高壓電力電纜最高承受電壓位置的方法。
為了達到上述目的,本發明所採用的技術方案是:
一種計算空載高壓電力電纜最高承受電壓位置的方法,包括以下步驟:
根據電纜結構參數計算電纜迴路單位長度電阻、電感、電容和導納參數;
根據電阻、電感、電容和導納參數,計算出電纜單位長度的衰減係數和相位係數;
將衰減係數和相位係數與正弦波函數結合,構建正弦波傳播函數;
根據正弦波傳播函數,運用正弦波傳播規律構建電纜沿線各點最高承受電壓計算模型,計算出電纜最高承受電壓位置。
電纜電阻、電感、電容和導納參數的計算公式為
Rθ=[R1+R2+(R1κ1+R2κ2)(θ-20)]/n
G=ω'C×tanδ
其中,Rθ為電纜迴路在溫度θ下的直流電阻,R1為在溫度θ時,單位長度電纜線芯導體直流電阻,R2為在溫度θ時,單位長度電纜護套導體直流電阻,κ1為每一絕對溫度θ時電纜線芯導體材料對應的溫度係數,κ2為每一絕對溫度θ時電纜護套導體材料對應的溫度係數,n為迴路中並聯的線路數;
L為電纜迴路單位長度電感,μ0為真空磁導率,s為電纜線芯間的幾何平均距離,Dco為電纜導體外徑;
C為電纜迴路單位長度電容,ε0為真空介電常數,εr為絕緣材料的相對介電常數,Di為所試電纜金屬護套的內徑,Dn為電纜迴路中與其他並聯線路距離,Dc為電纜線芯外徑;
G為電纜迴路單位長度電導,ω′為工頻角頻率,tanδ為材料的損耗因數。
衰減係數和相位係數的計算公式為,
其中,α、β分別表示衰減係數和相位係數,ω為角頻率。
正弦波傳播函數U+(x,t)為,
0≤t≤tm
其中,t為傳播時間,tm為波形的時間,A為波形幅值,x為正弦波從電纜入射端開始向電纜終端方向上的位移,為正弦波源產生波形的初始相位,g(t-x/v)為定義的函數,v表示波速。
電纜沿線各點電壓為,
U(x,t)=U-(x,t)+U+(x,t)
其中,U-(x,t)為反射波函數,
其中,l為電纜長度。
當tm≥(2l+λ)/v時:
電纜任何一點都同時經歷正弦波和反射波至少一個周期,則
0≤δ≤π
x′=l-x
其中,x′為波形傳播位置距離電纜終端的距離,λ表示波長,
當U(x,t)最大時,解得的x即為電纜最高承受電壓位置;
當tm<(2l+λ)/v時:
正弦波初次從電纜始端傳向電纜終端時,反射波函數U_(x,t)=0;
0≤t≤tm
0≤x≤vt
其中,
若0≤x′≤tmv/2-λ,區間內電纜任何一點都同時經歷正弦波和反射波至少一個周期;
0≤δ≤π
x′=l-x
其中,
若0<tmv/2-λ<x′≤tmv/2或者0<x′≤tmv/2<λ,區間內電纜任何一點上正弦波和反射波經歷小於2π的(tmv-2x')β/2相位角變化;
(l-x)/v+tm/2+x/v≤t≤tm+x/v
0≤δ≤π
x′=l-x
其中,
當max[U1(x,t),U2(x,t),U3(x,t)]最大時,解得的x即為電纜最高承受電壓位置。
本發明所達到的有益效果:本發明解決了目前沒有計算空載高壓電力電纜最高承受電壓位置方法的問題,可為長距離空載電纜線路中,高壓工頻操作、變頻耐壓試驗、阻尼震蕩波試驗等出現的電纜瞬態擊穿故障分析提供分析指導,並可為模擬故障電纜線路擊穿事故試驗提供數據依據。
附圖說明
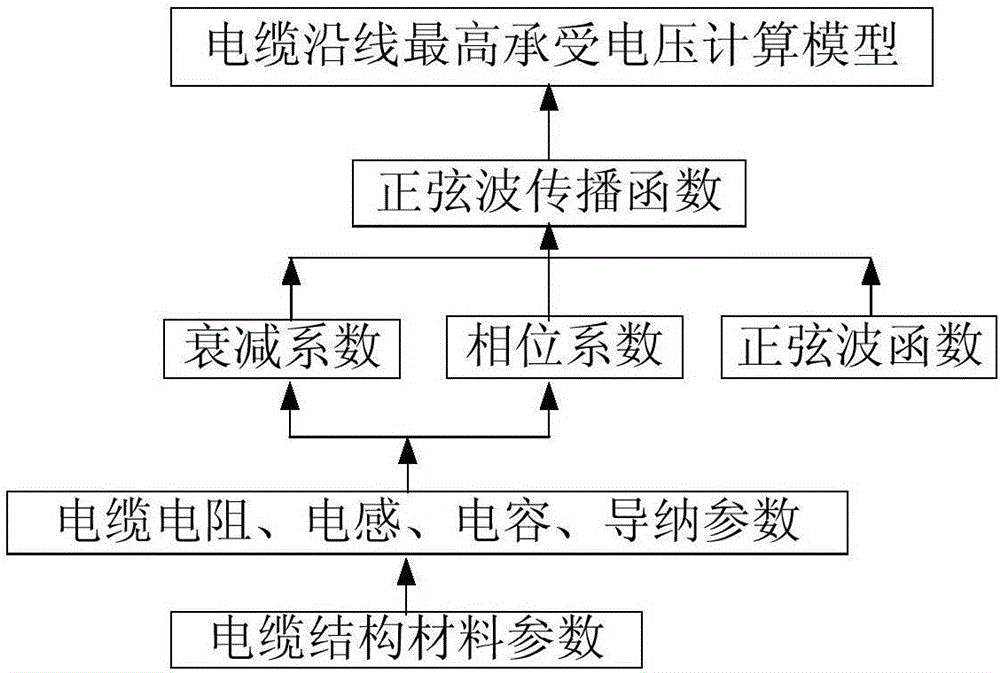
圖1為本發明的流程圖。
圖2為電纜傳播簡化分析圖。
具體實施方式
下面結合附圖對本發明作進一步描述。以下實施例僅用於更加清楚地說明本發明的技術方案,而不能以此來限制本發明的保護範圍。
如圖1所示,一種計算空載高壓電力電纜最高承受電壓位置的方法,包括以下步驟:
1)根據電纜結構參數計算電纜迴路單位長度電阻、電感、電容和導納參數。
具體計算公式如下:
Rθ=[R1+R2+(R1κ1+R2κ2)(θ-20)]/n
其中,Rθ為電纜迴路在溫度θ下的直流電阻,R1為在溫度θ時,單位長度電纜線芯導體直流電阻,R2為在溫度θ時,單位長度電纜護套導體直流電阻,κ1為每一絕對溫度θ時電纜線芯導體材料對應的溫度係數,κ2為每一絕對溫度θ時電纜護套導體材料對應的溫度係數,n為迴路中並聯的線路數。
其中,L為電纜迴路單位長度電感,μ0為真空磁導率,s為電纜線芯間的幾何平均距離,Dco為電纜導體外徑。
其中,C為電纜迴路在單位長度電容,ε0為真空介電常數,εr為絕緣材料的相對介電常數,Di為所試電纜金屬護套的內徑,Dn為電纜迴路中與其他並聯線路距離,Dc為電纜線芯外徑。
G=ω'C×tanδ
其中,G為電纜迴路單位長度電導,ω′為工頻角頻率,tanδ為材料的損耗因數。
2)根據電阻、電感、電容和導納參數,計算出電纜單位長度的衰減係數和相位係數。
根據分布參數電路原理計算推導得出:
其中,α、β分別表示衰減係數和相位係數,ω為角頻率。
3)將衰減係數和相位係數與正弦波函數結合,構建正弦波傳播函數。
正弦波函數f(t)為:
0≤t≤tm
其中,t為傳播時間,tm為波形的時間,A為波形幅值,為正弦波源產生波形的初始相位。
因此正弦波傳播函數U+(x,t)為:
0≤t≤tm
其中,x為正弦波從電纜入射端開始向電纜終端方向上的位移,g(t-x/v)為定義的函數,v=ω/β表示波速。
4)根據正弦波傳播函數,運用正弦波傳播規律構建電纜沿線各點最高承受電壓計算模型,計算出電纜最高承受電壓位置。
正弦波在電纜中傳播具有如下特點:
1、正弦波形時間小於在兩倍長度電纜的傳播時間時,並且電纜空載可認為電纜兩端阻抗無窮大,正弦波會在電纜內發生多次反射,由於存在波形衰減,當電纜衰減係數大,電纜最高電壓點可能出現在電纜的首端位置;而當電纜衰減係數小,電纜最高電壓點可能出現入射波和反射波的疊加部分,由於存在波形衰減,因此入射波和反射波最大疊加電壓出現在電纜終端初次反射時,電纜終端至入射端方向上入射波和反射波的疊加區間。
2、當正弦波形時間大於在兩倍長度電纜的傳播時間,電纜任何一點都同時經歷正弦波和反射波至少一個周期,電纜末端空載,可認為阻抗無窮大,而入射端連接電源,阻抗可認為為零,因此,正弦波在電纜中傳播,電壓反射波從終端到達電纜入射端再次反射時,電壓反射係數為0,故而最大電壓只需考慮正弦波沿電纜從入射端傳到終端,反射波從終端傳到入射端這段時間內的電纜沿線最大電壓即可。
綜上,電纜沿線最大電壓承受點可能出現在電纜入射端或者電纜終端至入射端方向上入射波和反射波的疊加區間。
定義電纜長度為l,電纜傳播簡化分析圖如圖2所示,由於電纜末端空載,可認為阻抗無窮大,因此終端電壓折射係數為0,電壓反射係數為1。因此,反射波函數U_(x,t)為:
其中,0≤x≤l。
電纜沿線各點電壓為:
U(x,t)=U_(x,t)+U+(x,t)
當tm≥(2l+λ)/v時:
電纜任何一點都同時經歷正弦波和反射波至少一個周期,則
0≤δ≤π
x′=l-x
其中,x′為波形傳播位置距離電纜終端的距離,λ表示波長,T為周期,
當U(x,t)最大時,解得的x即為電纜最高承受電壓位置。
當tm<(2l+λ)/v時:
正弦波初次從電纜始端傳向電纜終端時,反射波函數U_(x,t)=0;
0≤t≤tm
0≤x≤vt
其中,
若0≤x′≤tmv/2-λ,區間內電纜任何一點都同時經歷正弦波和反射波至少一個周期;
0≤δ≤π
x′=l-x
其中,
若0<tmv/2-λ<x′≤tmv/2或者0<x′≤tmv/2<λ,區間內電纜任何一點上正弦波和反射波經歷小於2π的(tmv-2x')β/2相位角變化;
(l-x)/v+tm/2+x/v≤t≤tm+x/v
0≤δ≤π
x′=l-x
其中,
當max[U1(x,t),U2(x,t),U3(x,t)]最大時,解得的x即為電纜最高承受電壓位置。
為了進一步說明上述方法,對以下案例進行分析。
目標電纜結構參數如表一所示;
表一目標電纜結構參數
其中,D1和D2分別表示迴路中所試電纜與另外兩根並聯電纜的距離。
根據方法中的公式可解得如下參數,具體如表二所示:
表二根據電纜結構參數獲得的參數
正弦波函數f(t)為:
f(t)=1.28×103sin(2000πt+90°)
0≤t≤1.5×10-3
根據正弦波函數可知:
0≤x≤5.3×104
tmv/2-λ=-0.25λ<0,因此無需計算U2(x,t);
當0<x'≤tmv/2=0.75λ時,則
max[U1(x,t),U2(x,t),U3(x,t)]=1.28×105。
上述方法是通過計算電纜單位長度線路的衰減係數以及相位係數,結合電纜正弦波形參數建立正弦行波在電纜中傳播的傳播函數,運用三角函數運算方法建立關於電纜軸向承受電壓的數學模型,從而計算出電纜最高承受電壓點的位置。
上述方法解決了目前沒有計算空載高壓電力電纜最高承受電壓位置方法的問題,可為長距離空載電纜線路中,高壓工頻操作、變頻耐壓試驗、阻尼震蕩波試驗等出現的電纜瞬態擊穿故障分析提供分析指導,並可為模擬故障電纜線路擊穿事故試驗提供數據依據。
以上所述僅是本發明的優選實施方式,應當指出,對於本技術領域的普通技術人員來說,在不脫離本發明技術原理的前提下,還可以做出若干改進和變形,這些改進和變形也應視為本發明的保護範圍。
