一種空間複雜柔性結構多體系統動力學建模與計算方法與流程

2023-05-28 05:41:16 1

本發明屬於空間結構動力學計算技術領域，具體涉及一種空間複雜柔性結構多體系統動力學建模與計算方法。

背景技術：

近年來，我國航天科技發展迫切需要掌握柔性空間結構在軌展開技術，以滿足衛星通信、天基對地觀測和深空探測等重大需求。這類空間結構一般主要由剛性杆、柔性梁、板、殼和柔性繩索等構件組成，各構件間除鉸節點處的位置約束外，還存在大量同步、滑移等非線性約束。同時這類空間結構展開尺度大、柔軟部件多、構形複雜，其展開過程會呈現系統大範圍運動與柔軟部件大變形之間的非線性耦合動力學。美國、俄羅斯等國在其航天任務中，曾發生多起結構展開失敗。由於這類結構的展開動力學地面實驗難度大、無法完全抵消重力影響，故其展開過程的動力學數值模擬是確保結構展開成功的關鍵技術。

針對此類空間複雜柔性結構多體系統，經典多體系統動力學方法的研究思路是:在柔性結構體上附著浮動坐標系,以其相對於絕對坐標系的運動來描述柔體大範圍運動,通過模態縮聚近似描述柔性結構體相對浮動坐標系的變形。該類方法一般引入小轉動、小變形假設,將柔性結構體的彈性變形與剛體位移分開考慮，進行解耦處理。通常這種方法只能靠大量增加單元數量來處理柔性結構體的大變形、大位移問題,從而導致計算規模大、計算效率低。此外,這種方法不能精確地反映空間複雜柔性結構展開過程中的力學本質特性。由於空間複雜柔性結構多體系統存在很多非線性約束、運動副間隙及複雜的載荷條件,目前商業軟體在系統動力學建模、數值求解效率等方面存在許多困難。

技術實現要素：

有鑑於此，本發明提供了一種空間複雜柔性結構多體系統動力學建模與計算方法，為柔性結構多體系統提供了一種簡單有效的動力學建模方法，提高了計算效率。

實現本發明的技術方案如下：

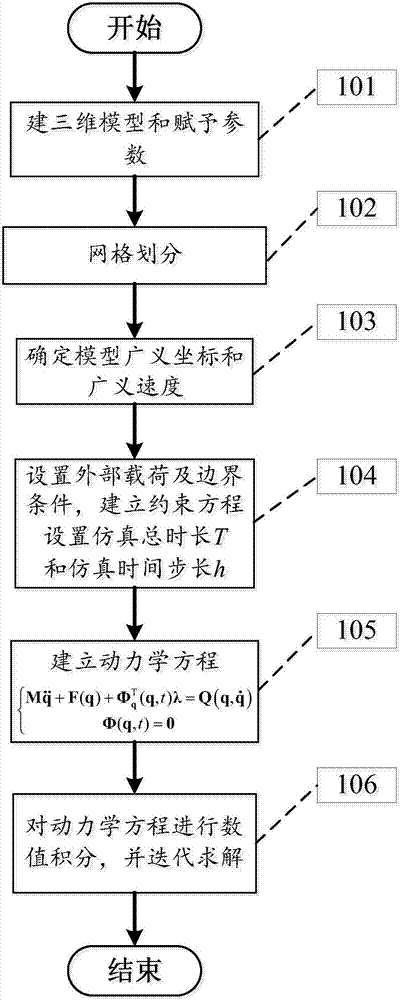
步驟101：建三維模型和賦予參數：根據所要求解的實物，建立該實物的三維模型，輸入所建模型的材料參數、幾何參數以及空間結構拓撲關係；

步驟102：網格劃分：基於步驟101賦予參數後的三維模型進行網格劃分，利用絕對節點坐標法、幾何精確法或等幾何分析方法確定網格單元類型，將劃分後的三維模型定義為網格模型；

步驟103：根據步驟102劃分的網格確定各個網格單元的初始節點位置和初始節點速度，基於單元初始節點位置和初始節點速度計算網格單元廣義坐標向量q和廣義速度向量

步驟104：根據步驟103獲得的廣義坐標向量和廣義速度向量，設置網格模型的外部載荷及邊界條件，基於網格模型的邊界條件，建立網格模型的約束方程，並設置仿真總時長t以及仿真時間步長h；

步驟105：根據步驟102-104獲得的網格單元類型、廣義坐標向量、廣義速度向量和約束方程，基於第一類拉格朗日方程建立多體系統動力學方程，如下：

其中m為系統質量陣，為廣義加速度向量，f(·)為系統的彈性力向量，q(·)為系統的廣義外力向量，φ(·)和φq(·)分別為步驟104獲得的約束方程向量和約束方程向量對廣義坐標向量的偏導數矩陣，(·)q為函數對廣義坐標向量的偏導數，λ為拉格朗日乘子向量，t為仿真時間,t∈[0,t]，t為矩陣轉置；

步驟106：對所建的多體系統動力學方程進行時域離散，獲得時域離散後的多體系統動力學方程，對離散後的多體系統動力學方程進行迭代，並對迭代過程中生成的線性方程組進行並行求解，輸出廣義坐標向量q以及拉格朗日乘子向量λ，至此完成對空間複雜柔性結構多體系統動力學問題的建模與求解。

進一步地，所述步驟106具體為：

步驟601：根據步驟105得到多體系統動力學方程，對多體系統動力學方程進行離散，離散後多體系統動力學方程見公式(2)；

步驟602：對離散後的多體系統動力學方程進行求解得到第n+1步的廣義坐標向量qn+1、廣義速度向量和拉格朗日乘子向量λn+1；

步驟603：根據步驟602判斷時間tn+1是否小於總仿真時間t，若當前時間tn+1不小於總仿真時間t，則計算停止；否則，n自動加1，重複執行步驟601-603，計算廣義坐標向量qn+1、廣義速度向量令時間tn+1＝tn+h，直到tn+1大於或等於t，輸出廣義坐標向量qn+1以及拉格朗日乘子向量λn+1，其中qn+1為q，λn+1為λ。

進一步地，對多體系統動力學方程進行離散採用如下方法：

應用廣義-alpha隱式時間積分算法對多體系統動力學方程進行如下離散：

其中

式(4)中，β和γ為決定計算精度與效率的算法參數，取γ≥1/2和β≥(1/2+γ)2/4。n為迭代次數，h為仿真時間步長，為了耗散系統高頻響應，引入新的算法矢量參數a，其中矢量參數a滿足關係：

式(4)和式(5)中各參數的選取方法如下:

其中為算法的譜半徑，αm和αf均為廣義-alpha隱式時間積分算法參數。

進一步地，本步驟中用q均代表qn+1，λ均代表λn+1，所述步驟602進一步包括：

步驟6021：設置求解精度tol；

步驟6022：採用newton-rapson迭代求解所述公式(2)，獲得如下線性代數方程組：

其中δq和δλ是當前時刻t系統廣義坐標向量和拉格朗日乘子向量的增量，其中

和為滿足如下關係的算法參數:

其中，和均為中間變量，ψ和γ均為中間矩陣，為函數對廣義速度向量的偏導數；

步驟6023：根據步驟6021獲得的線性方程組計算當前殘差向量的模r；

其中，||·||為模；

步驟6024：根據步驟6022對線性方程組的求解更新當前廣義坐標向量以及拉格朗日乘子向量；

步驟6025：根據步驟6023獲得的殘差向量模判斷迭代結果是否收斂，若r>tol，則根據步驟6024更新獲得的廣義坐標向量以及拉格朗日乘子向量，重複執行步驟6022-6025，直至rtol，則根據步驟6024更新獲得的廣義坐標向量以及拉格朗日乘子向量，重複執行步驟6022-6025，直至r<tol或r＝tol，輸出步驟6024獲得的廣義坐標向量q以及拉格朗日乘子向量λ，並存儲。至此完成對某環形桁架索網天線機構展開動力學建模與高效計算。圖9給出了某環形桁架天線展開過程中6個指定時刻的系統構型，該圖明顯展示了環形桁架天線展開過程中的不同步現象相應的地面試驗結果驗證了該數值仿真結果的有效性。

綜上所述，以上僅為本發明的較佳實施例而已，並非用於限定本發明的保護範圍。凡在本發明的精神和原則之內，所作的任何修改、等同替換、改進等，均應包含在本發明的保護範圍之內。