一種用於評價梁橋失效模式的方法與流程
2023-06-22 00:32:06 6
本發明屬於橋梁結構抗震技術領域,尤其是一種用於評價梁橋失效模式的方法。
背景技術:
美國二十世紀90年代末共有五百多座橋梁發生失效,這些失效中以鋼梁橋和鋼桁架橋所佔比例最多為50%,第二多的是混凝土梁橋、板橋佔11%。橋梁的服役期要遠多於橋梁的施工期間,這是橋梁的服役期成為橋梁失效發生的主要時期的主要原因。在外力作用下是導致大多數橋梁失效的原因,由外部作用(人為因素及自然因素)造成的橋梁失效數量眾多,其中人為因素主要有:大型貨車超載、輪船撞擊、車輛爆炸等;自然因素主要有:地震、洪水、驟風等。
當作用在結構上的地震力超過結構失效的定義值或判定標準時即認為結構失效,結構損傷發展的過程就是整個結構失效的過程;橋梁在各種不利情況的作用下,橋梁可能出現的各種失效模式,但目前未有合適的方法對各失效模式進行統計分析,找出橋梁的薄弱部位及最弱失效模式,為橋梁進行改造優化,從而用最為經濟和合理的方式,以提高橋梁結構的抗震性能。
技術實現要素:
本發明的目的為解決現有技術的不足,提供一種用於評價梁橋結構體系失效模式的方法,根據本發明的評價梁橋結構體系失效模式的方法能夠有效地對梁橋結構體系的失效模式進行統計分析,找出橋梁的薄弱部位及最弱失效模式,為橋梁進行改造優化,從而用最為經濟和合理的方式來提高橋梁結構的抗震性能。
為了解決上述技術問題,本發明採用如下技術方案:
一種用於評價梁橋結構體系失效模式的方法,包括以下步驟:
(一)選用n條能夠反映地震動中存在的不確定性且峰值地面加速度分布在一定強度範圍內的地震動,其中n為大於15的為整數;
(二)建立橋梁的有限元模型,對梁橋結構體系中的支座和橋墩墩底這兩個最容易失效的部位進行定義失效的判定指標信息;
(三)引用加權秩和比法綜合了n條地震動作用下的橋梁的失效模式的評價信息,分析給出具有統計意義的失效模式,並尋找出橋梁結構體系的最弱失效模式。
優選的,在所述步驟(二)中,所述定義失效的判定指標信息是根據橋梁所採用的材料、尺寸截面、支座類型及基礎形式進行建立逼近真實情況的有限元模型,分別定義橋梁支座和橋墩底部的失效的判定指標信息,然後引用加權秩和比法綜合了各條地震動作用下的橋梁的失效模式的評價信息,分析給出具有統計意義的失效模式。
優選的,所述步驟(三)中,尋找出橋梁結構體系的最弱失效模式如下方式進行:首先假設在失效模式事件集i=1,2,...,n中存在一個最大集且最大集滿足:
使得:
從而得到:
公式(3)為對應於最大事件集的失效模式,也稱為橋梁結構體系的最弱失效模式;
優選的,所述步驟(二)中,建立橋梁的有限元模型採用abaqus有限元軟體建立該梁橋結構體系的三維有限元模型。
與現有技術相比,本發明具有如下有益效果:
本發明的方法綜合了n條地震動的評價信息,解決了傳統結構地震失效模式優化目標單一的問題,給出具有統計意義的失效模式,對橋梁的失效模式進行控制,減小橋梁地震中的損傷,有利於震後快速恢復橋梁的功能,對減輕地震災害和進行震後有效的抗震救災具有重要的意義。
附圖說明
圖1是本發明具體實施例的橋梁體系結構簡圖;
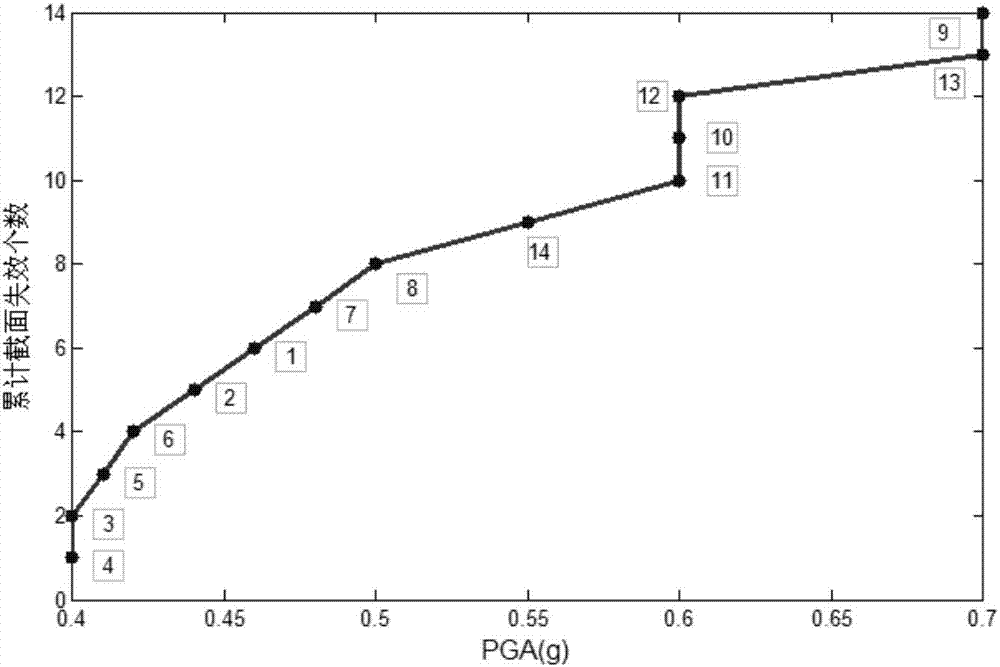
圖2是橋梁構件失效順序分布圖;
有關附圖標記的說明:
①-⑦為1-7#橋墩的同側支座單元;為1-7#橋墩的墩底單元;1#、7#墩為橋梁的邊墩;2#、6#墩為橋梁的過渡墩;3#、4#、5#墩為橋梁的中墩。
具體實施方式
下面結合具體實施例,對本發明作進一步詳細的闡述,但本發明的實施方式並不局限於實施例表示的範圍。這些實施例僅用於說明本發明,而非用於限制本發明的範圍。此外,在閱讀本發明的內容後,本領域的技術人員可以對本發明作各種修改,這些等價變化同樣落於本發明所附權利要求書所限定的範圍。
下面結合附圖,對本發明做進一步地詳細說明,但本發明的實施方式不僅限於此。
一種用於評價梁橋結構體系失效模式的方法,包括以下步驟:
(一)在增量動力(incrementaldynamicanalysis,ida)方法中。選用n條能夠反映地震動中存在的不確定性且峰值地面加速度(peakgroundacceleration,pda)分布在一定強度範圍內的地震動,其中n為大於15的整數;
(二)建立橋梁的有限元模型,對梁橋結構體系中的支座和橋墩墩底這兩個最容易失效的部位進行定義失效的判定指標信息;所述定義失效的判定指標是根據橋梁所採用的材料、尺寸截面、支座類型及基礎形式進行建立逼近真實情況的有限元模型,然後分別基於位移和修正的park-ang的損傷理論分別定義橋梁支座和橋墩底部的失效的判定指標;
修正的park-ang的損傷理論:
βe=[0.37n0+0.36(kp-0.2)2]×0.9ρw(2)
其中,ds為損傷參數;my、φy為橋墩在靜力單調荷載作用下的屈服彎矩和屈服曲率;φm為橋墩在地震作用下的最大曲率;φu為橋墩在靜力單調荷載作用下的極限曲率;βe為組合參數;∫deh為構件累計耗散的能量;n0為橋墩的縱向軸壓比;ρw為體積配箍率;kp為歸一化的受拉鋼筋配筋率,kp=ρtfy/(0.85fc),fy為鋼筋抗拉屈服強度,fc為混凝土抗壓強度,ρt為受拉鋼筋配筋率;
(三)引用加權秩和比法(wrsr)綜合了n條地震動作用下的橋梁結構體系失效模式的判定指標信息,分析給出具有統計意義的失效模式,並尋找出橋梁結構體系的最弱失效模式。
在本發明中,所述的加權秩和比法(wrsr)滿足:
其中,i=1,2,…,n;j=1,2,…,n;rij表示第i行第j列元素的秩。
當各個評價指標的權重不同時,計算加權秩和比wrsr的公式為:
且滿足,
wj為第j個評價指標的權重。
在本發明中,尋找出橋梁結構體系的最弱失效模式如下方式進行:首先假設在失效模式事件集中存在一個最大集
使得:
從而得到:
公式(8)為對應於最大事件集的失效模式,也稱為橋梁結構體系的最弱失效模式;橋梁結構體系的最弱失效模式的工程意義在於要麼失效模式伴隨其它任何失效模式出現,要麼失效模式單獨出現。
作為本發明的進一步說明,ida方法現已廣泛用於估計結構在遭遇不同強度地震動作用下的響應和分析結構的整體抗倒塌能力。wrsr是一種直觀、有效的統計分析方法,且對資料無特殊要求,使用靈活簡便,適用於統計資料的再分析。此方法計算用的數值是秩次,可以消除異常值的幹擾,它融合了參數分析的方法,結果比單純採用非參數法更為精確。秩和比法既可以對評價對象的優劣進行直接排序,還可以根據需要分檔排序,而且引入各個指標的權重係數後得到的加權秩和比可以在一定程度上消除主觀偏見,更具有客觀與實際意義。
在本發明中,評價梁橋結構體系失效模式的具體方法如下:
步驟一:在ida方法中,選用16條足夠反映地震動中存在的不確定性且pda分布在一個較寬的固定強度範圍內的地震動,如表1所示。
表1選取的地震動參數
步驟二:建立橋梁的有限元模型,對橋梁中支座、橋墩墩底這兩個最容易失效的部位定義失效的判定指標,更具體的是根據實際橋梁所採用的材料、尺寸截面、支座類型及基礎形式等建立接近真實情況的有限元模型,然後分別基於位移和修正的park-ang的損傷理論分別定義橋梁支座和橋墩底部的失效的判定指標。橋梁模型為6跨110m隔震連續梁橋,1-7#橋墩(依次從左往右)高度墩高分別為23.7m,23.4m,23.8m,23.5m,23.1m,23.1m,23.7m;橋梁寬度33.1m;墩柱長和寬為10.0×3.5m,厚度為1.0m,橋墩採用c50混凝土,hrb335鋼筋,配筋率為1.12%;承臺的長、寬和高為15.4×11.1×4.5m。採用abaqus有限元軟體建立該橋梁結構體系的三維有限元模型,如圖1所示,在圖1中,①-⑦為1-7#橋墩的同側支座單元,為1-7#橋墩的墩底單元。1#、7#墩為橋梁的邊墩,2#、6#墩為橋梁的過渡墩,3#、4#、5#墩為橋梁的中墩。在對橋梁樁底縱向輸入地震動時,取橋梁一側支座作為研究對象並對連接單元進行編號①-⑦,橋梁兩側的支座具有對稱性,在縱向地震作用下,響應情況幾乎一樣,故僅取一側支座作為分析對象。對於單柱墩的連續梁橋,橋墩柱的底部區域為塑性鉸區域,取各墩墩底為研究對象,並對橋墩構件進行編號對於鉛芯隔震橡膠支座可以採用雙摺線彈塑性彈簧單元進行模擬,橋墩採用纖維梁單元,支座採用conn3d2連接單元模擬,其他構件採用梁單元b31模擬。
1)lrb支座失效的判斷
參照《公路橋梁抗震設計細則》(jtg/tb02-01-2008),對鉛芯橡膠支座進行驗算時,在地震作用下產生的剪切應變應小於支座橡膠層厚度的2.5倍。《城市橋梁抗震設計規範》僅要求進行e2地震作用下的分析與驗算,並要求橡膠型的隔震支座,在地震作用下產生的剪切應變應在250%以下,還要進行穩定性驗算。故取支座剪切變形為250%時作為支座失效的判定值。
2)橋墩失效的判斷
表2修正park-ang構件損傷分級及參數
註:在本發明的表2中ds=0.75時,認為構件失效。
步驟三:引用加權秩和比法(wrsr)綜合了16條地震動作用下的橋梁的失效模式的評價信息,分析給出具有統計意義的失效模式,並找出了橋梁的最弱失效模式。
1)加權秩和比的統計結果:計算連續梁橋模型在16條地震動不同加速度峰值下各構件的損傷值,並根據損傷值的變化情況來確定各單元的失效順序,結果如表3所示。對於gm-1地震動作用下橋梁邊墩支座失效後,該橋墩之所以失效,是由於隨著pga的增大時,橋墩的失效時間將早於橋梁支座的時間。另外由於橋梁支座沒有達到極限位移狀態,仍然能傳遞上部結構的內力。其他地震動作用下的情況,支座失效後橋墩仍然失效的原因類似。
表3各地震動作用下橋梁各單元的失效次序
按照公式(4)計算各地震動作用下橋梁出現的失效單元的加權秩和比,權重係數w取為單元該地震動的失效峰值加速度與所有地震動的失效峰值加速度總和的比值,並根據其先後失效順序編秩。根據加權秩和比的大小,其數值越小,說明該構件越先失效,反之,構件失效越靠後;根據加權秩和比和失效順序的對應關係,如表4所示,可以得到本工程隔震連續梁橋最終失效模式為:即該橋梁中墩的隔震支座先失效,接著是橋梁過渡墩支座失效,然後是1#邊墩底部和1#墩的支座失效,最後是7#邊墩支座與7#橋墩墩底失效。
按照公式(4)計算各地震動作用下橋梁出現的失效單元的加權秩和比,權重係數w取為單元該地震動的失效峰值加速度與所有地震動的失效峰值加速度總和的比值,並根據其先後失效順序編秩。根據加權秩和比的大小,其數值越小,說明該構件越先失效,反之,構件失效越靠後;根據加權秩和比和失效順序的對應關係,如表4所示,可以得到本工程隔震連續梁橋最終失效模式為:即該橋梁中墩的隔震支座先失效,接著是橋梁過渡墩支座失效,然後是1#邊墩底部和1#墩的支座失效,最後是7#邊墩支座與7#橋墩墩底失效。
表4失效單元的加權秩和比
2)最弱失效模式分析
不同的地震動輸入下結構各構件失效時,所對應的pga均不同,且各構件的損傷量化指標ds值的大小也不同。經過分析,在遭受強度較小的地震作用下,結構構件的ds值先達到結構構件失效定義值0.75,結構構件最容易失效,即在gm-7作用下橋梁失效模式為橋梁的最弱失效模式,如圖2所示為構件在gm-7用下,構件失效順序及對應的pga。由圖2可知,橋梁最弱失效模式為:即首先是橋梁所有隔震支座先失效,其次是邊墩底部失效,然後是中墩失效,最後是過渡墩失效。
以上所述僅為發明的較佳實施例而已,並不用以限制本發明,凡在本發明的精神和原則之內,所作的任何修改、等同替換、改進等,均應包含在本發明的保護範圍之內。
